Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T17:51:46.788Z Has data issue: false hasContentIssue false
  • English
  • Français

GÖDEL DIFFEOMORPHISMS

Part of: Smooth dynamical systems: general theory Computability and recursion theory Proof theory and constructive mathematics

Published online by Cambridge University Press:  01 September 2020

MATTHEW FOREMAN
MATTHEW FOREMAN*
Affiliation:
MATHEMATICS DEPARTMENT UNIVERSITY OF CALIFORNIAIRVINE, CA, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1932, von Neumann proposed classifying the statistical behavior of differentiable systems. Joint work of B. Weiss and the author proved that the classification problem is complete analytic. Based on techniques in that proof, one is able to show that the collection of recursive diffeomorphisms of the 2-torus that are isomorphic to their inverses is 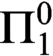$\Pi ^0_1$-hard via a computable 1-1 reduction. As a corollary there is a diffeomorphism that is isomorphic to its inverse if and only if the Riemann Hypothesis holds, a different one that is isomorphic to its inverse if and only if Goldbach’s conjecture holds and so forth. Applying the reduction to the 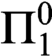$\Pi ^0_1$-sentence expressing “ZFC is consistent” gives a diffeomorphism T of the 2-torus such that the question of whether 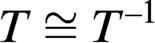$T\cong T^{-1}$ is independent of ZFC.

Keywords

diffeomorphismsanti-classificationrecursive reductions

MSC classification

Primary: 03D78: Computation over the reals
Secondary: 03F60: Constructive and recursive analysis 37C40: Smooth ergodic theory, invariant measures
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 26 , Issue 3-4 , December 2020 , pp. 219 - 223
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anzai, H., On an example of a measure preserving transformation which is not conjugate to its inverse. Proceedings of the Japan Academy, vol. 27 (1951), pp. 517–522.Google Scholar
Foreman, M., Gödel diffeomorphisms, preprint, 2020, arXiv:2009.06735.Google Scholar
Foreman, M., Rudolph, D. J., and Weiss, B., The conjugacy problem in ergodic theory. Annals of Mathematics (2), vol. 173 (2011), no. 3, pp. 1529–1586.CrossRefGoogle Scholar
Foreman, M. and Weiss, B., From odometers to circular systems: a global structure theorem. Journal of Modern Dynamics, vol. 15 (2019), pp. 345–423.CrossRefGoogle Scholar
Foreman, M. and Weiss, B., A symbolic representation for Anosov-Katok systems. Journal of Mathematical Analysis, vol. 137 (2019), no. 2, pp. 603–661.Google Scholar
Foreman, M. and Weiss, B., Measure preserving diffeomorphisms of the torus are unclassifiable, preprint, 2017, arXiv:1705.04414.Google Scholar
Furstenberg, H., Recurrence in Ergodic Theory and Combinatorial Number Theory, Princeton University Press, Princeton, NJ, 1981. M.B. Porter Lectures.CrossRefGoogle Scholar
Glasner, Eli, Ergodic Theory via Joinings, Mathematical Surveys and Monographs, vol. 110, American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Halmos, P. R., American Mathematical Society Math Reviews, 1951, MR47742.Google Scholar
Halmos, P. R., Lectures on Ergodic Theory, Chelsea Publishing Co., New York, 1960.Google Scholar
Hjorth, G., Classification and orbit equivalence relations, Mathematical Surveys and Monographs, vol. 75, American Mathematical Society, Providence, RI, 2000.Google Scholar
Hjorth, G., On invariants for measure preserving transformations. Fundamenta Mathematicae, vol. 169 (2001), no. 1, pp. 51–84.CrossRefGoogle Scholar
Katok, A., Combinatorial Constructions in Ergodic Theory and Dynamics, University Lecture Series, vol. 30, American Mathematical Society, Providence, RI, 2003.Google Scholar
Petersen, K., Ergodic Theory, Cambridge Studies in Advanced Mathematics, vol. 2, Cambridge University Press, Cambridge, 1989.Google Scholar
Rudolph, D. J., Fundamentals of Measurable Dynamics, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1990.Google Scholar
Shields, P. C., The Ergodic Theory of Discrete Sample Paths, Graduate Studies in Mathematics, vol. 13, American Mathematical Society, Providence, RI, 1996.Google Scholar
von Neumann, J., Zur Operatorenmethode in der klassischen Mechanik. Annals of Mathematics (2), vol. 33 (1932), no. 3, pp. 587–642.CrossRefGoogle Scholar
Walters, P., An Introduction to Ergodic Theory, Graduate Texts in Mathematics, vol. 79, Springer-Verlag, New York-Berlin, 1982.CrossRefGoogle Scholar
Weiss, B., Single Orbit Dynamics, CBMS Regional Conference Series in Mathematics, vol. 95, American Mathematical Society, Providence, RI, 2000.Google Scholar