Article contents
FINDING THE LIMIT OF INCOMPLETENESS I
Published online by Cambridge University Press: 16 April 2021
Abstract
In this paper, we examine the limit of applicability of Gödel’s first incompleteness theorem (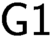 $\textsf {G1}$ for short). We first define the notion “
$\textsf {G1}$ for short). We first define the notion “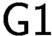 $\textsf {G1}$ holds for the theory
$\textsf {G1}$ holds for the theory  $T$”. This paper is motivated by the following question: can we find a theory with a minimal degree of interpretation for which
$T$”. This paper is motivated by the following question: can we find a theory with a minimal degree of interpretation for which 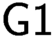 $\textsf {G1}$ holds. To approach this question, we first examine the following question: is there a theory T such that Robinson’s
$\textsf {G1}$ holds. To approach this question, we first examine the following question: is there a theory T such that Robinson’s  $\mathbf {R}$ interprets T but T does not interpret
$\mathbf {R}$ interprets T but T does not interpret 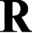 $\mathbf {R}$ (i.e., T is weaker than
$\mathbf {R}$ (i.e., T is weaker than  $\mathbf {R}$ w.r.t. interpretation) and
$\mathbf {R}$ w.r.t. interpretation) and 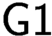 $\textsf {G1}$ holds for T? In this paper, we show that there are many such theories based on Jeřábek’s work using some model theory. We prove that for each recursively inseparable pair
$\textsf {G1}$ holds for T? In this paper, we show that there are many such theories based on Jeřábek’s work using some model theory. We prove that for each recursively inseparable pair 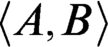 $\langle A,B\rangle $, we can construct a r.e. theory
$\langle A,B\rangle $, we can construct a r.e. theory 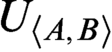 $U_{\langle A,B\rangle }$ such that
$U_{\langle A,B\rangle }$ such that 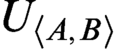 $U_{\langle A,B\rangle }$ is weaker than
$U_{\langle A,B\rangle }$ is weaker than 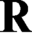 $\mathbf {R}$ w.r.t. interpretation and
$\mathbf {R}$ w.r.t. interpretation and 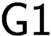 $\textsf {G1}$ holds for
$\textsf {G1}$ holds for 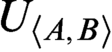 $U_{\langle A,B\rangle }$. As a corollary, we answer a question from Albert Visser. Moreover, we prove that for any Turing degree
$U_{\langle A,B\rangle }$. As a corollary, we answer a question from Albert Visser. Moreover, we prove that for any Turing degree 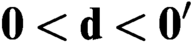 $\mathbf {0}< \mathbf {d}<\mathbf {0}^{\prime }$, there is a theory T with Turing degree
$\mathbf {0}< \mathbf {d}<\mathbf {0}^{\prime }$, there is a theory T with Turing degree 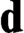 $\mathbf {d}$ such that
$\mathbf {d}$ such that 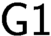 $\textsf {G1}$ holds for T and T is weaker than
$\textsf {G1}$ holds for T and T is weaker than 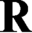 $\mathbf {R}$ w.r.t. Turing reducibility. As a corollary, based on Shoenfield’s work using some recursion theory, we show that there is no theory with a minimal degree of Turing reducibility for which
$\mathbf {R}$ w.r.t. Turing reducibility. As a corollary, based on Shoenfield’s work using some recursion theory, we show that there is no theory with a minimal degree of Turing reducibility for which 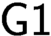 $\textsf {G1}$ holds.
$\textsf {G1}$ holds.
MSC classification
- Type
- Communication
- Information
- Copyright
- © The Association for Symbolic Logic 2021
References
REFERENCES
- 3
- Cited by



