Dimensions of Ordinals: Set Theory, Homology Theory, and the First Omega Alephs

Abstract

We describe an organizing framework for the study of infinitary combinatorics. This framework is Čech cohomology. It describes ZFC principles distinguishing among the ordinals of the form 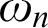$\omega _n$ . More precisely, this framework correlates each 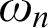$\omega _n$ with an 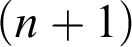$(n+1)$ -dimensional generalization of Todorcevic’s walks technique, and begins to account for that technique’s “unreasonable effectiveness” on 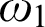$\omega _1$ .

We show in contrast that on higher cardinals 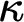$\kappa $ , the existence of these principles is frequently independent of the ZFC axioms. Finally, we detail implications of these phenomena for the computation of strong homology groups and higher derived limits, deriving independence results in algebraic topology and homological algebra, respectively, in the process.

Abstract prepared by Jeffrey Bergfalk.

E-mail: [email protected]