Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T20:31:20.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability in the Recursively Enumerable Degrees

Published online by Cambridge University Press:  15 January 2014

André Nies ,
Richard A. Shore  and
Theodore A. Slaman
André Nies
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA.E-mail:[email protected]
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA. E-mail: [email protected]
Theodore A. Slaman
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

§1. Introduction. Natural sets that can be enumerated by a computable function (the recursively enumerable or r.e. sets) always seem to be either actually computable (recursive) or of the same complexity (with respect to Turing computability) as the Halting Problem, the complete r.e. set K. The obvious question, first posed in Post [1944] and since then called Post's Problem is then just whether there are r.e. sets which are neither computable nor complete, i.e., neither recursive nor of the same Turing degree as K?

Let 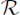be the r.e. degrees, i.e., the r.e. sets modulo the equivalence relation of equicomputable with the partial order induced by Turing computability. This structure is a partial order (indeed, an uppersemilattice or usl)with least element 0, the degree (equivalence class) of the computable sets, and greatest element 1 or 0′, the degree of K. Post's problem then asks if there are any other elements of .

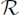The (positive) solution of Post's problem by Friedberg [1957] and Muchnik [1956] was followed by various algebraic or order theoretic results that were interpreted as saying that the structure 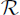was in some way well behaved:

Theorem 1.1 (Embedding theorem; Muchnik [1958], Sacks [1963]). Every countable partial ordering or even uppersemilattice can be embedded into .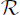

Theorem 1.2 (Sacks Splitting Theorem [1963b]). For every nonrecursive r.e. degreeathere are r.e. degreesb, c < asuch thatb ∨ c = a.

Theorem 1.3 (Sacks Density Theorem [1964]). For every pair of nonrecursive r.e. degreesa < bthere is an r.e. degreecsuch thata < c < b.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 2 , Issue 4 , December 1996 , pp. 392 - 404
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1984] Ambos-Spies, K., Jockusch, C. G. Jr., Shore, R. A., and Soare, R. I., An algebraic decomposition of the recursively enumerable degrees and the coincidence of several degree classes with the promptly simple degrees, Transactions of the American Mathematical Society, vol. 281, pp. 109–128.CrossRefGoogle Scholar
[1993] Ambos-Spies, K. and Shore, R. A., Undecidability and 1-types in the r.e. degrees, Annals of Pure and Applied Logic, vol. 63, pp. 3–37.CrossRefGoogle Scholar
[1996] Cooper, S. B., Beyond Gödel's theorem: the failure to capture information content, University of Leeds, Department of Pure Mathematics, preprint series, no. 4.Google Scholar
[1990] Downey, R. G., Lattice nonembeddings and initial segments of the recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 49, pp. 97–119.CrossRefGoogle Scholar
[1957] Friedberg, R. M., Two recursively enumerable sets of incomparable degrees of un-solvability, Proceeding ofthe National Academy ofSciences, vol. 43, pp. 236–238.CrossRefGoogle Scholar
[1982] Harrington, L. and Shelah, S., The undecidability of the recursively enumerable degrees (research announcement), Bulletin of the American Mathematical Society, New Series, vol. 6, pp. 79–80.CrossRefGoogle Scholar
[1993] Hodges, W., Model theory, Cambridge University Press, Cambridge, England.Google Scholar
[1983] Jockusch, C. G. Jr. and Shore, R. A., Pseudo-jump operators I: the r.e. case, Transactions ofthe American Mathematical Society, vol. 275, pp. 599–609.Google Scholar
[1966] Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceedings of the London Mathematical Society, vol. 16, pp. 537–569.CrossRefGoogle Scholar
[1966a] Lachlan, A. H., The impossibility of finding relative complements for recursively enumerable degrees, Journal of Symbolic Logic, vol. 31, pp. 434–454.Google Scholar
[1972] Lachlan, A. H., Embedding nondistributive lattices in the recursively enumerable degrees, Conference in Mathematical Logic, London, 1970 (Hodges, W., editor), LNMS, vol. 255, Springer-Verlag, Berlin, pp. 149–172.Google Scholar
[1975] Lachlan, A. H., A recursively enumerable degree which will not split over all lesser ones, Annals of Mathematical Logic, vol. 9, pp. 307–365.Google Scholar
[1980] Lachlan, A. H. and Soare, R. I., Not every finite lattice is embeddable in the recursively enumerable degrees, Advances in Mathematics, vol. 37, pp. 74–82.Google Scholar
[1956] Muchnik, A. A., On the unsolvability of the problem of reducibility in the theory of algorithms, Doklady Akademiya Nauk SSSR, New Series, vol. 108, pp. 29–32.Google Scholar
[1958] Muchnik, A. A., Solution of Post's reduction problem and of certain other problems in the theory of algorithms, Trudy Moskovskogo Matematicheskogo Obshchestva, vol. 7, pp. 391–405.Google Scholar
[1992] Nies, A., Definability and undecidability in recursion theoretic semilattices, Ph.D. thesis , Universität Heidelberg.Google Scholar
[1944] Post, E. L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50, pp. 284–316.Google Scholar
[1971] Robinson, R. W., Interpolation and embedding in the recursively enumerable degrees, Annals of Mathematics. Second Series, vol. 93, pp. 285–314.Google Scholar
[1963] Sacks, G. E., Degrees of unsolvability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, NJ.Google Scholar
[1963a] Sacks, G. E., Recursive enumerability and the jump operator, Transactions of the American Mathematical Society, vol. 108, pp. 223–239.Google Scholar
[1963b] Sacks, G. E., On the degrees less than 0′, Annals of Mathematics. Second Series, vol. 77, pp. 211–231.Google Scholar
[1964] Sacks, G. E., The recursively enumerable degrees are dense, Annals of Mathematics. Second Series, vol. 80, pp. 300–312.Google Scholar
[1966] Sacks, G. E., Degrees of unsolvability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, NJ, second ed.Google Scholar
[1965] Shoenfield, J. R., An application of model theory to degrees of unsolvability, Symposium on the theory ofmodels (Addison, J. W., Henkin, L., and Tarski, A., editors), North-Holland, Amsterdam, pp. 359–363.Google Scholar
[1979] Shore, R. A., The homogeneity conjecture, Proceedings of the National Academy of Sciences, vol. 76, pp. 4218–4219.Google Scholar
[1981] Shore, R. A., The theory of the degrees below 0′, Journal of the London Mathematical Society, vol. 76, pp. 1–14.Google Scholar
[1982] Shore, R. A., Finitely generated codings and the degrees r.e. in a degree d, Proceedings of the American Mathematical Society, vol. 84, pp. 256–263.Google Scholar
[1982a] Shore, R. A., On homogeneity and definability in the first order theory of the Turing degrees, Journal of Symbolic Logic, vol. 47, pp. 8–16.Google Scholar
[1990] Shore, R. A. and Slaman, T. A., Working below a low2 recursively enumerable degree , Archive for Mathematical Logic, vol. 29, pp. 201–211.CrossRefGoogle Scholar
[1991] Slaman, T. A., Degree structures, Proceedings of the International Congress on Mathematics, Kyoto 1990, Springer-Verlag, pp. 303–316.Google Scholar
[1987] Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[1988] Weinstein, B. J., On embeddings of the 1-3-1 into the recursively enumerable degrees, Ph.D. thesis , University of California, Berkeley.Google Scholar
[1966] Yates, C. E. M., A minimal pair of recursively enumerable degrees, Journal of Symbolic Logic, vol. 31, pp. 159–168.Google Scholar