Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T01:22:16.047Z Has data issue: false hasContentIssue false
  • English
  • Français

An Interpolation Theorem

Published online by Cambridge University Press:  15 January 2014

Martin Otto
Martin Otto*
Affiliation:
Mathematisches Grundlagen Der Informatik Rwth Aachen, Ahornstrasse 55, D-52074, Aachen, Germany.E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Lyndon's Interpolation Theorem asserts that for any valid implication between two purely relational sentences of first-order logic, there is an interpolant in which each relation symbol appears positively (negatively) only if it appears positively (negatively) in both the antecedent and the succedent of the given implication. We prove a similar, more general interpolation result with the additional requirement that, for some fixed tuple 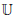of unary predicates U, all formulae under consideration have all quantifiers explicitly relativised to one of the U. Under this stipulation, existential (universal) quantification over U contributes a positive (negative) occurrence of U.

It is shown how this single new interpolation theorem, obtained by a canonical and rather elementary model theoretic proof, unifies a number of related results: the classical characterisation theorems concerning extensions (substructures) with those concerning monotonicity, as well as a many-sorted interpolation theorem focusing on positive vs. negative occurrences of predicates and on existentially vs. universally quantified sorts.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 6 , Issue 4 , December 2000 , pp. 447 - 462
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, J., A preservation theorem for interpretations, Proceedings of the Cambridge summer school in mathematical logic 1971 (Mathias, A. et al., editors), Lecture Notes in Mathematics, vol. 337, Springer-Verlag, 1973, pp. 618–621.CrossRefGoogle Scholar
[2] van Benthem, J., Information transfer across Chu spaces, Logic Journal of the IGPL, vol. 8 (11 2000), pp. 719–731.CrossRefGoogle Scholar
[3] Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., North-Holland, 1990.Google Scholar
[4] Craig, W., Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory, The Journal of Symbolic Logic, vol. 22 (1957), pp. 269–285.CrossRefGoogle Scholar
[5] Feferman, S., Lectures on proof theory, Proceedings of the summer school in logic, Leeds 67 (Löb, M., editor), Lecture Notes in Mathematics, vol. 70, Springer-Verlag, 1968, pp. 1–107.Google Scholar
[6] Feferman, S., Applications of many-sorted interpolation theorems, Proceedings of the Tarski symposium (Henkin, L. et al., editors), AMS Proceedings of Symposia in Pure Mathematics, vol. XXV, American Mathematical Society, 1974, pp. 205–223.CrossRefGoogle Scholar
[7] Feferman, S., Ah, Chu!, JFAK. Essays dedicated to Johan van Benthem on the occasion of his 50th birthday (Gerbrandy, J., Marx, M., Rijke, M. de, and Venema, Y., editors), Amsterdam University Press, 1999, CD-ROM, see http://turing.wins.uva.nl/j50/cdrom/.Google Scholar
[8] Flum, J., First-order logic and its extensions, Proceedings of the international summer institute and logic colloquium, Kiel 1974 (Müller, G. et al., editors), Lecture Notes in Mathematics, vol. 499, Springer-Verlag, 1975, pp. 248–310.Google Scholar
[9] Hodges, W., Model theory, Cambridge University Press, 1993.CrossRefGoogle Scholar
[10] Lyndon, R. C., An interpolation theorem in the predicate calculus, Pacific Journal of Mathematics, vol. 9 (1959), pp. 129–142.CrossRefGoogle Scholar
[11] Motohashi, N., Two theorems on mix-relativization, Proceedings of the Japan Academy, vol. 49 (1973), no. 3, pp. 161–163.Google Scholar
[12] Stern, J., A new look at the interpolation problem, The Journal of Symbolic Logic, vol. 40 (1975), no. 1, pp. 1–13.CrossRefGoogle Scholar