Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T02:28:16.822Z Has data issue: false hasContentIssue false
  • English
  • Français

An Application of Category-Theoretic Semantics to the Characterisation of Complexity Classes Using Higher-Order Function Algebras

Published online by Cambridge University Press:  15 January 2014

Martin Hofmann
Martin Hofmann*
Affiliation:
Fachbereich Mathematik, Technische Universität Darmstadt, Schlossgartenstrasse 7, 64289 Darmstadt, Germany.E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We use the category of presheaves over PTIME-functions in order to show that Cook and Urquhart's higher-order function algebra PVω defines exactly the PTIME-iunctions. As a byproduct we obtain a syntax-free generalisation of PTIME-computability to higher types.

By restricting to sheaves for a suitable topology we obtain a model for intuitionistic predicate logic with 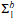-induction over PVω and use this to re-establish that the provably total functions in this system are polynomial time computable. Finally, we apply the category-theoretic approach to a new higher-order extension of Bellantoni-Cook's system BC of safe recursion.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 3 , Issue 4 , December 1997 , pp. 469 - 486
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bellantoni, Stephen and Cook, Stephen, New recursion-theoretic characterization of thepolytime functions, Computational Complexity, vol. 2 (1992), pp. 97–110.Google Scholar
[2] Buss, Samuel R., Bounded arithmetic, Bibliopolis, 1986.Google Scholar
[3] Cook, S. and Urquhart, A., Functional interpretations of feasibly constructive arithmetic, Annals of Pure and Applied Logic, vol. 63 (1993), pp. 103–200.Google Scholar
[4] Despeyroux, J., Pfenning, F., and Schürmann, C., Primitive recursion for higher-order abstract syntax, Technical Report CMU-CS-96-172, Carnegie Mellon University, 1996.Google Scholar
[5] Ehrhard, Thomas and Colson, Loïc, On strong stability and higher-order sequentiality, Proceedings of the 9th symposium logic in computer science (LICS), Paris, France, IEEE, 1994, pp. 103–109.Google Scholar
[6] Harnik, Victor, Provably total functions of intuitionistic bounded arithmetic, Journal of Symbolic Logic, vol. 57 (1992), no. 2, pp. 466–477.Google Scholar
[7] Hofmann, Martin, A mixed modal/linear lambda calculus with applications to Bellantoni-Cook safe recursion,presentedat Computer Science Logic '97, Aarhus, Denmark, submitted to the Proceedings.Google Scholar
[8] Jung, Achim and Tiuryn, Jerzy, A new characterisation of lambda definability, Typed lambda calculi and applications (TLCA '93) (Bezem, M. and Groote, J. F., editors), Springer Lecture Notes in Computer Science, vol. 664, 1993, pp. 245–257.Google Scholar
[9] Lambek, Joachim and Scott, Philip, Introduction to higher-order categorical logic, Cambridge University Press, 1986.Google Scholar
[10] Leivant, Daniel and Marion, Jean-Yves, Ramified recurrence and computational complexity IV: Predicative functionals and poly-space, 1997, manuscript.Google Scholar
[11] Mazur, S., Computable analysis, Rozprawy Matematyczne, vol. 33 (1963).Google Scholar
[12] Moerdijk, Ieke and Lane, Saunders Mac, Sheaves in geometry and logic. A first introduction to topos theory, Springer-Verlag, 1992.Google Scholar
[13] Mulry, Philip S., The topos of recursive sets, Ph.D. thesis , State University of New York at Buflalo, 1980.Google Scholar
[14] Otto, Jim, Complexity doctrines, Ph.D. thesis , McGill University, 1995.Google Scholar
[15] Statman, R., Logical relations and the typed λ-calculus, Information and Control, vol. 65 (1985), pp. 85–97.Google Scholar