No CrossRef data available.
Article contents
Algebraic and Model Theoretic Properties of O-minimal Exponential Fields
Published online by Cambridge University Press: 28 February 2022
Abstract
An exponential 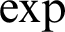 $\exp $
on an ordered field
$\exp $
on an ordered field 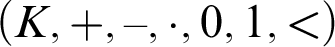 $(K,+,-,\cdot ,0,1,<)$
is an order-preserving isomorphism from the ordered additive group
$(K,+,-,\cdot ,0,1,<)$
is an order-preserving isomorphism from the ordered additive group 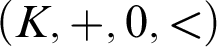 $(K,+,0,<)$
to the ordered multiplicative group of positive elements
$(K,+,0,<)$
to the ordered multiplicative group of positive elements 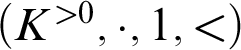 $(K^{>0},\cdot ,1,<)$
. The structure
$(K^{>0},\cdot ,1,<)$
. The structure 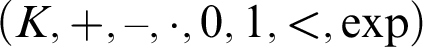 $(K,+,-,\cdot ,0,1,<,\exp )$
is then called an ordered exponential field (cf. [6]). A linearly ordered structure
$(K,+,-,\cdot ,0,1,<,\exp )$
is then called an ordered exponential field (cf. [6]). A linearly ordered structure 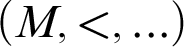 $(M,<,\ldots )$
is called o-minimal if every parametrically definable subset of M is a finite union of points and open intervals of M.
$(M,<,\ldots )$
is called o-minimal if every parametrically definable subset of M is a finite union of points and open intervals of M.
The main subject of this thesis is the algebraic and model theoretic examination of o-minimal exponential fields 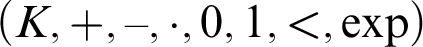 $(K,+,-,\cdot ,0,1,<,\exp )$
whose exponential satisfies the differential equation
$(K,+,-,\cdot ,0,1,<,\exp )$
whose exponential satisfies the differential equation 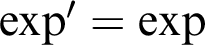 $\exp ' = \exp $
with initial condition
$\exp ' = \exp $
with initial condition 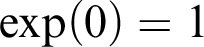 $\exp (0) = 1$
. This study is mainly motivated by the Transfer Conjecture, which states as follows:
$\exp (0) = 1$
. This study is mainly motivated by the Transfer Conjecture, which states as follows:
Any o-minimal exponential field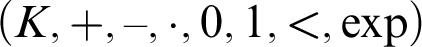 $(K,+,-,\cdot ,0,1,<,\exp )$
whose exponential satisfies the differential equation
$(K,+,-,\cdot ,0,1,<,\exp )$
whose exponential satisfies the differential equation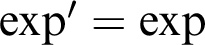 $\exp ' = \exp $
with initial condition
$\exp ' = \exp $
with initial condition $\exp (0)=1$
is elementarily equivalent to
$\exp (0)=1$
is elementarily equivalent to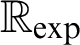 $\mathbb {R}_{\exp }$
.
$\mathbb {R}_{\exp }$
.
Here, 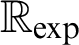 $\mathbb {R}_{\exp }$
denotes the real exponential field
$\mathbb {R}_{\exp }$
denotes the real exponential field 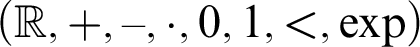 $(\mathbb {R},+,-,\cdot ,0,1,<,\exp )$
, where
$(\mathbb {R},+,-,\cdot ,0,1,<,\exp )$
, where 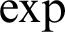 $\exp $
denotes the standard exponential
$\exp $
denotes the standard exponential 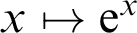 $x \mapsto \mathrm {e}^x$
on
$x \mapsto \mathrm {e}^x$
on 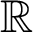 $\mathbb {R}$
. Moreover, elementary equivalence means that any first-order sentence in the language
$\mathbb {R}$
. Moreover, elementary equivalence means that any first-order sentence in the language 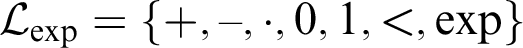 $\mathcal {L}_{\exp } = \{+,-,\cdot ,0,1, <,\exp \}$
holds for
$\mathcal {L}_{\exp } = \{+,-,\cdot ,0,1, <,\exp \}$
holds for 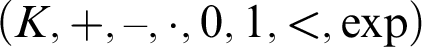 $(K,+,-,\cdot ,0,1,<,\exp )$
if and only if it holds for
$(K,+,-,\cdot ,0,1,<,\exp )$
if and only if it holds for 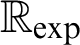 $\mathbb {R}_{\exp }$
.
$\mathbb {R}_{\exp }$
.
The Transfer Conjecture, and thus the study of o-minimal exponential fields, is of particular interest in the light of the decidability of 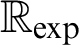 $\mathbb {R}_{\exp }$
. To the date, it is not known if
$\mathbb {R}_{\exp }$
. To the date, it is not known if 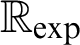 $\mathbb {R}_{\exp }$
is decidable, i.e., whether there exists a procedure determining for a given first-order
$\mathbb {R}_{\exp }$
is decidable, i.e., whether there exists a procedure determining for a given first-order 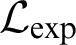 $\mathcal {L}_{\exp }$
-sentence whether it is true or false in
$\mathcal {L}_{\exp }$
-sentence whether it is true or false in 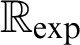 $\mathbb {R}_{\exp }$
. However, under the assumption of Schanuel’s Conjecture—a famous open conjecture from Transcendental Number Theory—a decision procedure for
$\mathbb {R}_{\exp }$
. However, under the assumption of Schanuel’s Conjecture—a famous open conjecture from Transcendental Number Theory—a decision procedure for 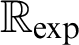 $\mathbb {R}_{\exp }$
exists (cf. [7]). Also a positive answer to the Transfer Conjecture would result in the decidability of
$\mathbb {R}_{\exp }$
exists (cf. [7]). Also a positive answer to the Transfer Conjecture would result in the decidability of 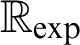 $\mathbb {R}_{\exp }$
(cf. [1]). Thus, we study o-minimal exponential fields with regard to the Transfer Conjecture, Schanuel’s Conjecture, and the decidability question of
$\mathbb {R}_{\exp }$
(cf. [1]). Thus, we study o-minimal exponential fields with regard to the Transfer Conjecture, Schanuel’s Conjecture, and the decidability question of 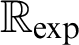 $\mathbb {R}_{\exp }$
.
$\mathbb {R}_{\exp }$
.
Overall, we shed light on the valuation theoretic invariants of o-minimal exponential fields—the residue field and the value group—with additional induced structure. Moreover, we explore elementary substructures and extensions of o-minimal exponential fields to the maximal ends—the smallest elementary substructures being prime models and the maximal elementary extensions being contained in the surreal numbers. Further, we draw connections to models of Peano Arithmetic, integer parts, density in real closure, definable Henselian valuations, and strongly NIP ordered fields.
Parts of this thesis were published in [2–5].
Abstract prepared by Lothar Sebastian Krapp
E-mail: [email protected]
MSC classification
- Type
- Thesis Abstracts
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Association for Symbolic Logic
Footnotes
Supervised by Salma Kuhlmann.



