Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T02:24:31.939Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Complexity of the Classification Problem for Torsion-Free Abelian Groups of Finite Rank

Published online by Cambridge University Press:  15 January 2014

Simon Thomas
Simon Thomas*
Affiliation:
Mathematics Department, Rutgers University, 110 Frelinghuysen Road, Piscataway, New Jersey 08854-8019, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we shall discuss some recent contributions to the project [15, 14, 2, 18, 22, 23] of explaining why no satisfactory system of complete invariants has yet been found for the torsion-free abelian groups of finite rank n ≥ 2. Recall that, up to isomorphism, the torsion-free abelian groups of rank n are exactly the additive subgroups of the n-dimensional vector space ℚn which contain n linearly independent elements. Thus the collection of torsion-free abelian groups of rank at most n can be naturally identified with the set S (ℚn) of all nontrivial additive subgroups of ℚn. In 1937, Baer [4] solved the classification problem for the class S(ℚ)of rank 1 groups as follows.

Let ℙ be the set of primes. If G is a torsion-free abelian group and 0 ≠ x ϵ G, then the p-height of x is defined to be

hx(p) = sup{n ϵ ℕ ∣ There exists y ϵ G such that pny = x} ϵ ℕ ∪{∞}; and the characteristic χ (x) of x is defined to be the function

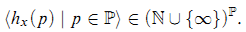
Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 7 , Issue 3 , September 2001 , pp. 329 - 344
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Adams, S. R., Trees and amenable equivalence relations, Ergodic Theory and Dynamical Systems, vol. 10 (1990), pp. 1–14.CrossRefGoogle Scholar
[2] Adams, S. R. and Kechris, A. S., Linear algebraic groups and countable Borelequivalence relations, Journal of the American Mathematical Society, vol. 13 (2000), pp. 909–943.CrossRefGoogle Scholar
[3] Adams, S. R. and Spatzier, R. J., Kazhdan groups, cocycles and trees, American Journal of Mathematics, vol. 112 (1990), pp. 271–287.CrossRefGoogle Scholar
[4] Baer, R., Abelian groups without elements of finite order, Duke Mathematical Journal, vol. 3 (1937), pp. 68–122.CrossRefGoogle Scholar
[5] Billingsley, P., Probability and measure, 2nd ed., Wiley, New York, 1986.Google Scholar
[6] Borel, A., Linear algebraic groups: Second enlarged edition, Graduate texts in mathematics, vol. 126, Springer-Verlag, 1991.Google Scholar
[7] Corner, A. L. S., Every countable reduced torsion-free ring is an endomorphism ring, Proceedings of the London Mathematical Society, vol. 13 (1963), pp. 687–710.CrossRefGoogle Scholar
[8] Dougherty, R., Jackson, S., and Kechris, A. S., The structure of hyperfinite Borel equivalence relations, Transactions of the American Mathematical Society, vol. 341 (1994), pp. 193–225.CrossRefGoogle Scholar
[9] Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology and von Neumann algebras, I, Transactions of the American Mathematical Society, vol. 234 (1977), pp. 289–324.CrossRefGoogle Scholar
[10] Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures, The Journal of Symbolic Logic, vol. 54 (1989), pp. 894–914.CrossRefGoogle Scholar
[11] Fuchs, L., Infinite abelian groups, Pure and applied mathematics, vol. 36, Academic Press, 1970.Google Scholar
[12] Furman, A., Orbit equivalence rigidity, Annals of Mathematics, vol. 150 (1999), pp. 1083–1108.CrossRefGoogle Scholar
[13] Harrington, L., Kechris, A. S., and Louveau, A., A Glimm-Effros dichotomy for Borel equivalence relations, Journal of the American Mathematical Society, vol. 3 (1990), pp. 903–927.CrossRefGoogle Scholar
[14] Hjorth, G., Around nonclassifiability for countable torsion-free abelian groups, Abelian groups and modules, Dublin, 1998, Trends in Mathematics, Birkhäuser, Basel, 1999, pp. 269–292.Google Scholar
[15] Hjorth, G. and Kechris, A. S., Borel equivalence relations and classification of countable models, Annals of Pure and Applied Logic, vol. 82 (1996), pp. 221–272.CrossRefGoogle Scholar
[16] Jackson, S., Kechris, A. S., and Louveau, A., Countable Borel equivalence relations, preprint, 2000.Google Scholar
[17] Jónsson, B., On direct decompositions of torsion-free abelian groups, Mathematica Scandinavica, vol. 7 (1959), pp. 361–371.CrossRefGoogle Scholar
[18] Kechris, A. S., On the classification problem for rank 2 torsion-free abelian groups, to appear in The Journal of the London Mathematical Society.Google Scholar
[19] Król, M., The automorphism groups and endomorphism rings of torsion-free abelian groups of rank two, Dissertationes Mathematicae (Rozprawy Matematyczne), vol. 55 (1967), pp. 1–76.Google Scholar
[20] Kurosh, A. G., Primitive torsionsfreie abelsche Gruppen vom endlichen Range, Annals of Mathematics, vol. 38 (1937), pp. 175–203.CrossRefGoogle Scholar
[21] Malcev, A. I., Torsion-free abelian groups of finite rank, Matematicheskiǐ Sbornik, vol. 4 (1938), pp. 45–68, Russian.Google Scholar
[22] Thomas, S., On the complexity of the classification problem for torsion-free abelian groups of rank two, to appear in Acta Mathematica.Google Scholar
[23] Thomas, S., The classification problem for torsion-free abelian groups of finite rank, preprint, 2000.Google Scholar
[24] Thomas, S. and Velickovic, B., On the complexity of the isomorphism relation for finitely generated groups, Journal of Algebra, vol. 217 (1999), pp. 352–373.CrossRefGoogle Scholar
[25] Thomas, S., On the complexity of the isomorphism relation for fields of finite transcendence degree, to appear in Journal of Pure and Applied Algebra.Google Scholar
[26] Varadarajan, V. S., Groups of automorphisms of Borel spaces, Transactions of the American Mathematical Society, vol. 109 (1963), pp. 191–220.CrossRefGoogle Scholar
[27] Zimmer, R., Ergodic theory and semisimple groups, Birkhäuser, 1984.CrossRefGoogle Scholar