Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T13:35:34.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Models of Second-Order Zermelo Set Theory

Published online by Cambridge University Press:  15 January 2014

Gabriel Uzquiano
Gabriel Uzquiano*
Affiliation:
Department of Philosophy, University of Rochester, P. O. Box 270078 Rochester, New York 14627-0078, USAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In [12], Ernst Zermelo described a succession of models for the axioms of set theory as initial segments of a cumulative hierarchy of levels UαVα. The recursive definition of the Vα's is:

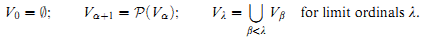
Thus, a little reflection on the axioms of Zermelo-Fraenkel set theory (ZF) shows that Vω, the first transfinite level of the hierarchy, is a model of all the axioms of ZF with the exception of the axiom of infinity. And, in general, one finds that if κ is a strongly inaccessible ordinal, then Vκ is a model of all of the axioms of ZF. (For all these models, we take ∈ to be the standard element-set relation restricted to the members of the domain.) Doubtless, when cast as a first-order theory, ZF does not characterize the structures 〈Vκ,∈∩(Vκ×Vκ)〉 for κ a strongly inaccessible ordinal, by the Löwenheim-Skolem theorem. Still, one of the main achievements of [12] consisted in establishing that a characterization of these models can be attained when one ventures into second-order logic. For let second-order ZF be, as usual, the theory that results from ZF when the axiom schema of replacement is replaced by its second-order universal closure. Then, it is a remarkable result due to Zermelo that second-order ZF can only be satisfied in models of the form 〈Vκ,∈∩(Vκ×Vκ)〉 for κ a strongly inaccessible ordinal.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 5 , Issue 3 , September 1999 , pp. 289 - 302
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bernays, Paul, A system of axiomatic set theory VI, Journal of Symbolic Logic, vol. 13 (1948), pp. 65–79.Google Scholar
[2] Bernays, Paul, A system of axiomatic set theory VII, Journal of Symbolic Logic, vol. 19 (1954), pp. 81–96.CrossRefGoogle Scholar
[3] Boolos, George, The advantages of honest toil over theft, Mathematics and mind, Oxford University Press, 1994.Google Scholar
[4] Drake, Frank, Set theory: An introduction to large cardinals, North-Holland, 1974.Google Scholar
[5] Felgner, Ulrich, Models of ZF-set theory, Lecture Notes in Mathematics, no. 223, Springer-Verlag, Berlin, 1971.CrossRefGoogle Scholar
[6] Fraenkel, Abraham, Bar-Hillel, Yehoshua, and Levy, Azriel, Foundations of set theory, North-Holland, 1973.Google Scholar
[7] Levy, Azriel, Basic set theory, Springer-Verlag, 1979.Google Scholar
[8] Montague, Richard, Set theory and higher-order logic, Formal systems and recursive functions (Crossley, J. and Dummett, M., editors), North-Holland, 1967, pp. 131–148.Google Scholar
[9] Moschovakis, Yiannis, Notes on set theory, Springer-Verlag, 1994.Google Scholar
[10] Rieger, L., A contribution to Gödel's axiomatic set theory, Czechoslovak Mathematical Journal, vol. 7 (1957), pp. 323–357.Google Scholar
[11] Scott, Dana, Axiomatizing set theory, Axiomatic set theory (Jech, Thomas, editor), Proceedings of Symposia in Pure Mathematics, vol. II, American Mathematical Society, 1974, pp. 207–214.Google Scholar
[12] Zermelo, Ernst, Über Grenzzahlen und Mengenbereiche: Neue Untersuchungen über die Grundlagen der Mengenlehre, Fundamenta Mathematicae, vol. 16 (1930), pp. 29–47.Google Scholar