Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T18:57:43.032Z Has data issue: false hasContentIssue false
  • English
  • Français

DISJUNCTIONS WITH STOPPING CONDITIONS

Part of: Proof theory and constructive mathematics Philosophical aspects of logic and foundations Nonstandard models

Published online by Cambridge University Press:  05 January 2021

ROMAN KOSSAK  and
BARTOSZ WCISŁO
ROMAN KOSSAK
Affiliation:
THE GRADUATE CENTER CITY UNIVERSITY OF NEW YORK 365 FIFTH AVENUE, NEW YORK, NY10016, USAE-mail: [email protected]
BARTOSZ WCISŁO
Affiliation:
INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES UL. ŚNIADECKICH 800-656WARSAW, POLANDE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

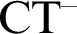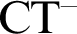We introduce a tool for analysing models of $\text {CT}^-$ , the compositional truth theory over Peano Arithmetic. We present a new proof of Lachlan’s theorem that the arithmetical part of models of $\text {CT}^-$ are recursively saturated. We also use this tool to provide a new proof of theorem from [8] that all models of 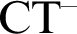$\text {CT}^-$ carry a partial inductive truth predicate. 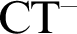Finally, we construct a partial truth predicate defined for a set of formulae whose syntactic depth forms a nonstandard cut which cannot be extended to a full truth predicate satisfying $\text {CT}^-$ .

Keywords

truth theoriestruth predicatessatisfaction classesPeano Arithmeticmodels of arithmeticrecursive saturation

MSC classification

Primary: 03H15: Nonstandard models of arithmetic
Secondary: 03F30: First-order arithmetic and fragments 03A99: None of the above, but in this section
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 27 , Issue 3 , September 2021 , pp. 231 - 253
Check for updates
Copyright
© 2021, Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cieśliński, C., ŁeŁyk, M., and WcisŁo, B., Models of ${{{PT}}\hspace{1.5pt}}^{-}$ with internal induction for total formulae . The Review of Symbolic Logic , vol. 10 (2017), no. 1, pp. 187–202.CrossRefGoogle Scholar
Enayat, A. and Pakhomov, F., Truth, disjunction, and induction. Archive for Mathematical Logic , vol. 58 (2019), pp. 753–766.Google Scholar
Enayat, A. and Visser, A., New constructions of satisfaction classes , Unifying the Philosophy of Truth (T. Achourioti, H. Galinon, J. Martínez Fernández, and K. Fujimoto, editors), Springer, Dordrecht, 2015, pp. 321–335.CrossRefGoogle Scholar
Kaye, R., Models of Peano Arithmetic , Clarendon Press, Oxford, 1991.Google Scholar
Kotlarski, H., Bounded induction and satisfaction classes . Zeitschrift für mathematische Logik und Grundlagen der Mathematik , vol. 32 (1986), pp. 531–544.CrossRefGoogle Scholar
Lachlan, A. H., Full satisfaction classes and recursive saturation . Canadian Mathmematical Bulletin , vol. 24 (1981), pp. 295–297.CrossRefGoogle Scholar
ŁeŁyk, M., Axiomatic Theories of Truth, Bounded Induction, and Reflection Principles . Ph.D. disseration, University of Warsaw, 2017.Google Scholar
ŁeŁyk, M. and WcisŁo, B., Models of weak theories of truth . Archive for Mathematical Logic , vol. 56 (2017), no. 5, pp. 453–474.CrossRefGoogle Scholar
Smith, S., Nonstandard syntax and semantics and full satisfaction classes for models of arithmetic , Ph.D. thesis, Yale University, 1984.Google Scholar
Smith, S. T., Nonstandard definability . Annals of Pure and Applied Logic , vol. 42 (1989), no. 1, pp. 21–43.CrossRefGoogle Scholar
WcisŁo, B., Understanding the strength of the compositional truth , Ph.D. thesis, University of Warsaw, 2018.Google Scholar