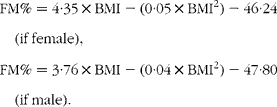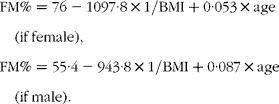Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T03:06:41.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Body composition predicted with a Bayesian network from simple variables

Published online by Cambridge University Press:  10 December 2010

Laurence Mioche ,
Caroline Bidot  and
Jean-Baptiste Denis
Laurence Mioche*
Affiliation:
INRA, UMR 1019 Nutrition Humaine, Theix, 63122Saint Genes Champanelle, France
Caroline Bidot
Affiliation:
INRA, Unité de Recherche MIA, 78352Jouy-en-Josas, France
Jean-Baptiste Denis
Affiliation:
INRA, Unité de Recherche MIA, 78352Jouy-en-Josas, France
*
*Corresponding author: Dr L. Mioche, email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

The relative contributions of fat-free mass (FFM) and fat mass (FM) to body weight are key indicators for several major public health issues. Predictive models could offer new insights into body composition analysis. A non-parametric equation derived from a probabilistic Bayesian network (BN) was established by including sex, age, body weight and height. We hypothesised that it would be possible to assess the body composition of any subject from easily accessible covariables by selecting an adjusted FFM value within a reference dual-energy X-ray absorptiometry (DXA) measurement database (1999–2004 National Health and Nutrition Examination Survey (NHANES), n 10 402). FM was directly calculated as body weight minus FFM. A French DXA database (n 1140) was used (1) to adjust the model parameters (n 380) and (2) to cross-validate the model responses (n 760). French subjects were significantly different from American NHANES subjects with respect to age, weight and FM. Despite this different population context, BN prediction was highly reliable. Correlations between BN predictions and DXA measurements were significant for FFM (R2 0·94, P < 0·001, standard error of prediction (SEP) 2·82 kg) and the percentage of FM (FM%) (R2 0·81, P < 0·001, SEP 3·73 %). Two previously published linear models were applied to the subjects of the French database and compared with BN predictions. BN predictions were more accurate for both FFM and FM than those obtained from linear models. In addition, BN prediction generated stochastic variability in the FM% expressed in terms of BMI. The use of such predictions in large populations could be of interest for many public health issues.

Keywords

Bayesian networksBody compositionFat massFat-free massDual-energy X-ray absorptiometryPredictionNon-parametric models
Type
Full Papers
Information
British Journal of Nutrition , Volume 105 , Issue 8 , 28 April 2011 , pp. 1265 - 1271
Copyright
Copyright © The Authors 2010

The relative contribution of fat-free mass (FFM) and fat mass (FM) to body weight is a relevant indicator for major public health issues(Reference Snijder, van Dam and Visser1, Reference Bender, Trautner and Spraul2). Due to the accumulation of excess fat tissue, the worldwide increase in the prevalence of obesity contributes to a high risk of metabolic disorders such as CVD and type 2 diabetes(Reference Flegal and Graubard3). In addition, FFM loss in ageing populations and its progression towards sarcopenia increase morbidity and mortality(Reference Gallagher, Ruts and Visser4–Reference Rolland, Czerwinski and Abellan Van Kan6). Accurate measurements of body composition can be obtained from reference methods, such as underwater weighing, dilution techniques and dual-energy X-ray absorptiometry (DXA). Although the use of such methods is widespread, their application is time consuming and expensive, and as a result, they are not relevant for use as a part of routine clinical examinations or population studies. Bioelectrical impedance has often been considered to be a convenient tool for body composition analysis. However, the recorded bioelectrical values (resistance and reactance) must be used in equations that are body shape specific, and accurate FFM and FM assessments require adjustments with a gold standard method(Reference Janssen, Heymsfield and Baumgartner7–Reference Kyle, Bosaeus and De Lorenzo10).

In contrast, simple anthropological measurements, such as body weight or BMI, cannot give a reliable quantification of body composition, although they are of predictive interest at a population level(Reference Flegal and Graubard3, Reference Gallagher, Heymsfield and Heo11–Reference Duggleby, Jackson and Godfrey13). Models that provide reliable predictions of body composition from very simple covariables are still needed. Because increasingly more information on body composition analysis is available, either directly from large surveys (e.g. National Health and Nutrition Examination Survey; NHANES) or indirectly through scientific publications, we investigated the potential of a non-parametric model derived from a Bayesian network (BN) to predict body composition. A BN provides a global joint probability distribution over a set of random variables(Reference Carlin and Louis14, Reference Albert, Grenier and Denis15). The ability to combine variables and the growing capabilities of computer calculations have made these models increasingly popular. Indeed, they have become of great use in quantitative risk assessment(Reference Albert, Grenier and Denis15–Reference Jeanpierre and Charpillet17). However, to our knowledge, such models have not been used for body composition analysis. Assuming a direct influence of sex, age, body weight and height on body composition(Reference Ellis18–Reference Jackson, Ellis and McFarlin21), we hypothesised that it might be possible to assess the body composition of any subject by selecting an adjusted FFM value from a DXA measurement database (DXA, 1999–2004 NHANES) with easily accessible covariables (sex, age, height and weight). The present study aims to present this new calculation concept and to validate BN predictions for FFM and FM against DXA measurements obtained from an independent sample of French subjects. A comparison with previously published linear models(Reference Gallagher, Heymsfield and Heo11, Reference Jackson, Stanforth and Gagnon22) was also performed.

Method

Reference database used for body composition analysis

All FFM values used for body composition predictions were extracted from the NHANES website (http://www.cdc.gov/nchs/about/major/nhanes/) for the 1999–2004 period (n 10 402). Subjects were characterised from the covariables (sex, age, height and weight) included in the model irrespective of ethnicity (Table 1).

Table 1 Population description in the databases used as the reference (National Health and Nutrition Examination Survey (NHANES)), for model adjustment (CHU-fit) and for validation (CHU-valid)

(Mean values and standard deviations)

CHU, Clermont-Ferrand University Hospital Centre; FFM, fat-free mass; FM, fat mass.

*  Mean values were significantly different between NHANES and CHU (valid or fit) within a sex group (P < 0·001).

†  Mean values were significantly different between CHU-fit and CHU-valid (P < 0·001).

For the current purpose, only subjects having a valid scan were included, and the mean value of five DXA measurements (Hologic QDR-4500) was considered. Lean mass values were increased by 5 % to overcome the initial reduction imposed on the entire NHANES database, as explained in the user guide (http://www.cdc.gov/nchs/nhanes/dxx/dxa.htm)(Reference Schoeller, Tylavsky and Baer23).

Independent body composition database for model fitting and validation

A database of 1140 French subjects (aged between 20 and 79 years and with BMI between 18·5 and 40 kg/m2) who had their body composition measured by DXA (Hologic QDR-4500) during routine examination at the Radiology Department of the Clermont-Ferrand University Hospital Centre (CHU) between 1998 and 2008 was used. From this database, two different subsets were defined to adjust parameters for FFM estimates (CHU-fit: 380 subjects), and the second was used to cross-validate model responses (CHU-valid: 760 subjects) (Table 1). Subsets were matched for sex and BMI distributions.

Fat-free mass adjustments

For each subject in the CHU-fit database, a subset of candidates was selected in the NHANES database using a BN equation, which included the age, body weight and height of the subject to predict.

A distance was computed from the covariables using the following formula:

\begin{eqnarray} D = \frac {\,max\,\left ( w _{a} d _{a}, w _{h} d _{h}, w _{w} d _{w}\right )}{ w _{a} + w _{h} + w _{w}}, \end{eqnarray}

where d a, d h, d w are the absolute values of the difference for age, height and weight, respectively, between the CHU subject to predict and the NHANES subjects of similar sex, and w a, w h, w w are associated weighting parameters for age, height and weight, respectively. A maximal distance (D m) was defined as the maximal selection limit. Only the NHANES subjects with D < D m were retained as candidates for prediction. When the closest NHANES subject was at a distance greater than D m, the predictive subset was empty, and no prediction was proposed.

For some combination of parameters (w a, w h, w w, D m), the coefficient of determination between FFM predictions and the corresponding DXA measurements, the standard error of prediction (SEP) and the prediction rate (ratio of the predicted individuals to the total number of individuals to predict) were simultaneously computed and used as criteria to estimate the quality of adjustment. Weighting parameters varying from 0·05 to 0·2 (age in years), 0·2 to 0·4 (height in cm) and 0·7 to 0·9 (weight in kg) were tested, with D m varying from 0·005 to 0·015 (arbitrary units). From a selected subset of candidates, the one having the median FFM value was used for prediction, and his/her FFM value was attributed to the CHU subject. Prediction was supported by the subject having the median FFM value of the subset of candidates instead of using the mean FFM value, which did not correspond to any particular subject. Increasing the number of candidates within the predictive subset extended the calculation process without producing a gain on the quality of prediction; thus, when the number of candidates exceeded fifty, only the fifty closest were kept. FM was then determined, assuming FM = body weight − FFM.

Extreme anthropometric situations were discarded, and model predictions were limited to subjects with BMI values between 18·5 and 40 kg/m2. In addition, model predictions were limited to subjects above 20 years of age to avoid growth influences on body composition analysis and below 79 years of age due to the weak representation of older subjects in the reference database. These restrictions were applied to the French databases (CHU-fit and CHU-valid) but not to the NHANES database. A candidate could be selected outside these limits when his/her covariables gave a distance below D m.

Comparisons with other predictive models

Predictions of the percentage of body fat (FM%) on CHU subjects were compared when obtained with either BN or multiple regression models. Two equations were considered as follows:

This last formula was proposed with an ethnic correction for Asian subjects, which was not used here. These equations were developed to predict FM%. Using a two-compartment model, they were applied to body weight to deduce FM and, consequently, FFM.

Statistical computations and analyses

Underlying calculations were processed using the Rebastaba package(Reference Denis, Delignette-Müller and Pouillot24) written in R (R Development Core Team, 2009), a language and environment for statistical computing (R Foundation for Statistical Computing, Vienna, Austria; ISBN 3-900051-07-0, URL http://www.R-project.org), which is available at http:/r-forge.r-project.org/projects/riskassessments/

The quality of prediction was globally assessed on both CHU-fit and CHU-valid databases by the SEP, which is defined as follows:

\begin{eqnarray} SEP = \sqrt {\frac {\sum (FFM_{measured} - FFM_{predicted})^{2}}{ n }}, \end{eqnarray}

where n is the number of subjects in the corresponding database.

Differences between population characteristics were analysed with Student's t test (XLstat 2008). Correlations between variables were calculated with Pearson's formula.

Results

Model parameter adjustments

The NHANES and CHU (fit and valid) subjects were significantly different for all variables (P < 0·001) with the exception of height (except for CHU-valid, where women were taller than those in the other groups). The NHANES subjects had greater body weight, BMI and FM than the French subjects. The CHU subjects had a slightly but significantly higher FFM (not significant for CHU-fit women) than the NHANES subjects. CHU-valid women had higher FFM values than the other female groups (Table 1). Therefore, BN prediction was analysed for subjects very distinct from the NHANES population.

Numerous combinations of weighting coefficients and D m were first considered. Among them, 125 effective combinations were scrutinised for the SEP and rate of prediction for the subjects belonging to the CHU-fit database. As expected, there were interactions between the SEP and the rate of prediction. The SEP decreased with D m until a minimum corresponding to the optimal fit between FFM predictions and DXA measurements, and then increased again with larger D m values (Fig. 1(a)). Decreasing D m led to an increase in the number of empty predictive subsets and consequently worsened the prediction rate. Reaching a predictive rate of 100 % was possible but reduced the quality of fit (SEP approximately 3 kg; Fig. 1(b)). The retained combination provided a compromise between the two criteria, with an SEP of 2·84 kg and a prediction rate of 99·21 %. The corresponding weighting parameters were as follows:

\begin{eqnarray} w _{a} = 0\cdot 08,\quad w _{h} = 0\cdot 2,\quad w _{w} = 0\cdot 5, \end{eqnarray}

with D m set at 0·0075.

Fig. 1 Variation of the standard error of prediction (SEP) over the tested combinations of parameters: (a) when varying the maximal distance (D m) used in the Bayesian network prediction (arbitrary units) and (b) its covariation with the rate of prediction.

Using these weighting parameters, the correlation between FFM predicted by the BN equation and FFM measured by DXA for the CHU-fit subjects was highly significant (R 2 0·94, P < 0·001). This combination of parameters was used in all subsequent calculations.

Accuracy of model prediction

The BN equation was cross-validated on the CHU-valid subjects. The subjects' repartition was fairly balanced between the CHU-fit and CHU-valid groups. No difference was observed for variables from men from the two databases. However, CHU-valid women were slightly taller and had higher FFM values than CHU-fit women. The covariables (age, height and weight) of the NHANES subjects selected as predictors were similar to those of the CHU subjects, and no difference was observed between the groups (Table 2).

Table 2 Population description for the CHU-valid subjects (n 760) and the National Health and Nutrition Examination Survey (NHANES) subjects used as predictors (n 760)*

(Mean values and standard deviations)

CHU, Clermont-Ferrand University Hospital Centre.

*  There were no significant differences between groups stratified by sex (P>0·001).

The FFM, FM and FM% values of the predictors were plotted against their respective experimental DXA counterparts (Fig. 2). Accuracy of BN prediction was compared with the two linear models, equations 1 and 2. The quality of fit was excellent in women for FFM (SEP 2·71 kg, R 2 0·86) and was superior to those obtained with equation 1 (SEP 3·64 kg, R 2 0·82) or equation 2 (SEP 3·73 kg, R 2 0·83). Similar trends were found for males; however, discrepancies between the three models were less pronounced for males than for females. All correlations were highly significant (Table 3). Because FM was deduced from FFM, the SEP was equivalent for FFM and FM. Correlations were still highly significant for FM%, although predictions were less closely fit to their experimental counterparts, and the SEP remained lower for BN prediction than those obtained with linear models.

Fig. 2 Scatter plots of Bayesian network prediction for fat-free mass (FFM) (a), fat mass (FM) (b) and the percentage of FM (FM%) (c) in terms of their experimental counterparts derived from dual-energy X-ray absorptiometry measurements on CHU-valid men (●) and women ( × ). The first bisectors are drawn (- - -).

Table 3 Quality of fit between fat-free mass (FFM) and the percentage of fat mass (FM%) as measured by dual-energy X-ray absorptiometry with the CHU-valid subjects and their counterparts predicted by the Bayesian network (BN), equation 1(Reference Jackson, Stanforth and Gagnon22) and equation 2(Reference Gallagher, Heymsfield and Heo11) for men and women*

CHU, Clermont-Ferrand University Hospital Centre; SEP, standard error of prediction.

*  All R 2 values were significant (P < 0·001).

When FM% was expressed in terms of BMI, a large inter-individual variability was observed with experimental measurements for both males and females. This variability was better described by the BN predictions than with other models (Fig. 3). The variability observed with equation 2 was introduced by the age effect, which was not sufficient by itself to describe the inter-individual variability. In contrast, the well-known sex difference in FM% in terms of BMI was well described by the three predictive models.

Fig. 3 Relationship between BMI and fat mass (FM), expressed as a percentage of body weight (FM%) measured by (a) dual-energy X-ray absorptiometry on CHU-valid men (●) and women ( × ) and the corresponding predictions for (b) the Bayesian network, (c) equation 1(Reference Jackson, Stanforth and Gagnon22) and (d) equation 2(Reference Gallagher, Heymsfield and Heo11). CHU, Clermont-Ferrand University Hospital Centre.

Discussion

The main objective of the present study was to investigate the potential use of a non-parametric equation derived from a BN to assess body composition with easily accessible covariables. BN are particularly useful in predicting events in a population when only part of the information is available or eventually provided as aggregated information. However, in the present study, BN prediction was validated in a context where all the covariables needed for prediction were known. It was shown that the BN enabled the precise prediction of the FFM of the French subjects (CHU) from body composition values recorded in the US population (NHANES). The first requirement in developing such a model was to have a validated database of body composition measurements. DXA is one of the gold standard methods for assessing body composition(Reference Heymsfield, Lohman and Wang25). The NHANES database, to our knowledge, is the largest database of DXA body composition measurements available for downloading. It offers a good reliability, with five replicates per subject recorded under validated procedures. The second requirement was to have a database of body composition analysis for a population similar to the population of interest. We were particularly interested in describing a French European population. Therefore, we used a French dataset to adjust the parameters of the BN equation. However, the equation could have been adjusted or applied to any other population. It is interesting to note that the NHANES database could be used to describe the body composition of a population of interest that differed in many aspects (age, weight and BMI). To predict the body composition of a subject, the BN equation returned an adjusted subset of candidates from which the one having the median FFM value was the predictor. His/her FFM value was attributed to the subject to predict, and FM was directly deduced as the body weight minus FFM. It would have been possible to do similar adjustments from any body compartment (fat, lean or bone mass). However, FFM was the most important body compartment, and the one most closely adjusted to the BN covariables(Reference Ellis18–Reference Deurenberg20). FM was then considered to be the adjusting variable. Bone mineral content represents the smallest compartment (about 3·5 % of weight). It was not considered to be a specific compartment but was included in FFM.

The potential outcomes associated with a reliable predictive model for body composition have been highlighted(Reference Snijder, van Dam and Visser1), and many attempts to describe body composition, particularly body fat, using linear models with simple variables have been proposed. They usually included BMI, and occasionally, age or ethnicity(Reference Deurenberg20, Reference Heymsfield, Lohman and Wang25, Reference Larsson, Henning and Lindroos26). It was thus interesting to compare the fit obtained with BN prediction and with linear predictive models when applied to the same population. Two robust and clearly described equations were used for comparison. Equation 1(Reference Jackson, Stanforth and Gagnon22) included a quadratic form of BMI that was irrespective of age, while equation 2(Reference Gallagher, Heymsfield and Heo11) included BMI, age and ethnicity, both with sex specificities. When applied to the CHU-valid subjects, the quality of FM% adjustments was very similar to those obtained in the original population context(Reference Gallagher, Heymsfield and Heo11, Reference Jackson, Stanforth and Gagnon22). For equation 2, the quality of fit varied from R 2 0·81, with SEP 4·31 %, in the original population to R 2 0·81, with SEP 4·01 %, for the CHU-valid subjects. For equation 1, when stratified by sex, the quality of fit varied from R 2 0·78, with SEP 4·63 %, in the original population to R 2 0·67, with SEP 4·73 %, for CHU-valid females and from R 2 0·68, with SEP 4·90 %, to R 2 0·59, with SEP 4·12 %, for CHU-valid males. The similarity of fit obtained with these two models in different populations confirms their robustness. For both body compartments (FFM and FM), BN prediction resulted in a better fit than linear models, especially for FFM, which was the adjusted compartment.

It is noteworthy that BN prediction was obtained without considering ethnicity. At first, ethnicity was included as a putative variable in the network due to its possible impact on FFM(Reference Gasperino, Wang and Pierson27, Reference Aloia, Vaswani and Feuerman28) and on fat deposition(Reference Lear, Humphries and Kohli29, Reference Kagawa, Kerr and Uchida30). In calculations not shown here, the quality of fit was analysed using either white, non-Hispanic subjects alone (as defined in the NHANES database) or all subjects, irrespective of ethnicity. Although the French population to predict (CHU) was mostly Caucasian, the best fit was obtained when the entire database was used (SEP 2·84 kg) rather than limited to white, non-Hispanic subjects (SEP 3·11 kg). The influence of ethnicity was, therefore, not included in the final model adjustment.

Sex differences observed in the relationships between BMI and FM% were similar to those previously described(Reference Jackson, Ellis and McFarlin21, Reference Flegal, Shepherd and Looker31). In contrast to other predictive linear models, BN prediction provided a stochastic picture of inter-individual variability, as illustrated by the relationship between BMI and FM% and could be useful to depict biological variability in any population of interest.

The BN equation is not a ready-to-use tool for straight application; instead, it should be considered as a new concept in the field of body composition assessments that can be improved in further releases. The applicability and accuracy of model predictions directly depend on the quality and quantity of the available information in the NHANES database. The predictive subset size varied from zero to fifty subjects. An empty subset meant that it was not possible to find a candidate in NHANES having the requested age, height and weight within the constraints imposed by the BN equation This prediction failure was rather low, and only four subjects out of 760 were not predicted. When the subset size equalled one, the FFM prediction was deduced from a single candidate with a higher risk of poor adjustment. These types of situations were more frequently found for extreme anthropometric values. Of the five predicted subjects with a subset of one (all female), two were taller than 180 cm, and two were shorter than 148 cm. Excluding subjects predicted from only one candidate, the quality of fit was slightly better for FFM (SEP 2·76 kg instead of 2·84 kg) but with a decreased rate of prediction (from 99·2 to 98·54 %). In contrast, a NHANES subject can be selected as a predictor for different CHU-valid subjects (six NHANES subjects were selected three times; sixty-seven were selected twice and 604 were involved in a single prediction). The number of replicates of a predictor depended on the covariable distribution of the population to predict. Retaining different model limits to avoid rare anthropometric situations could be a possible way to improve the model.

The quality of FFM predictions obtained with the BN model were similar to those obtained with bioelectrical impedance equations, where SEP varied from 2 to 3·6 kg(Reference Kushner32), suggesting that BN predictions could offer an interesting alternative to bioelectrical impedance measurements, usually considered as a convenient field measurement(Reference Lukaski, Johnson and Bolonchuk8). An additional interesting aspect of such a model derived from BN is the possibility of adding/removing variables. Waist circumference has a significant relationship with body fat(Reference Flegal, Shepherd and Looker31, Reference Boardley and Pobocik33). Thus, it might be worth considering its inclusion to improve the BN prediction of body composition.

Acknowledgements

The authors are grateful to Dr Ristori from the Radiology Department of the CHU for providing DXA data from the CHU database. The authors' responsibilities were as follows: L. M. was responsible for physiological statements, database collection and for writing the first draft of the manuscript. J.-B. D. and C. B. were responsible for model computations and statistics. L. M. and J.-B. D. designed the hypotheses. None of the authors had any conflict of interest regarding the manuscript. The present study was supported by a grant (ANSSD) from the INRA Human Nutrition Department, France.

References

1Snijder, MB, van Dam, RM, Visser, M, et al. (2006) What aspects of body fat are particularly hazardous and how do we measure them? Int J Epidemiol 35, 83–92.CrossRefGoogle Scholar
2Bender, R, Trautner, C, Spraul, M, et al. (1998) Assessment of excess mortality in obesity. Am J Epidemiol 147, 42–48.CrossRefGoogle ScholarPubMed
3Flegal, KM & Graubard, BI (2009) Estimates of excess deaths associated with body mass index and other anthropometric variables. Am J Clin Nutr 89, 1213–1219.CrossRefGoogle ScholarPubMed
4Gallagher, D, Ruts, E, Visser, M, et al. (2000) Weight stability masks sarcopenia in elderly men and women. Am J Physiol Endocrinol Metab 279, E366–E375.CrossRefGoogle ScholarPubMed
5Metter, EJ, Talbot, LA, Schrager, MR, et al. (2002) Skeletal muscle strength as a predictor of all-cause mortality in healthy men. J Gerontol A Biol Sci Med Sci 57, B359–B365.CrossRefGoogle ScholarPubMed
6Rolland, Y, Czerwinski, S, Abellan Van Kan, G, et al. (2008) Sarcopenia: its assessment, etiology, pathogenesis, consequences and future perspectives. J Nutr Health Aging 12, 433–450.CrossRefGoogle ScholarPubMed
7Janssen, I, Heymsfield, SB, Baumgartner, RN, et al. (2000) Estimation of skeletal muscle mass by bioelectrical impedance analysis. J Appl Physiol 89, 465–471.CrossRefGoogle ScholarPubMed
8Lukaski, HC, Johnson, PE, Bolonchuk, WW, et al. (1985) Assessment of fat-free mass using bioelectrical impedance measurements of the human body. Am J Clin Nutr 41, 810–817.CrossRefGoogle ScholarPubMed
9Clasey, JL, Kanaley, JA, Wideman, L, et al. (1999) Validity of methods of body composition assessment in young and older men and women. J Appl Physiol 86, 1728–1738.CrossRefGoogle Scholar
10Kyle, UG, Bosaeus, I, De Lorenzo, AD, et al. (2004) Bioelectrical impedance analysis – part I: review of principles and methods. Clin Nutr 23, 1226–1243.CrossRefGoogle ScholarPubMed
11Gallagher, D, Heymsfield, SB, Heo, M, et al. (2000) Healthy percentage body fat ranges: an approach for developing guidelines based on body mass index. Am J Clin Nutr 72, 694–701.CrossRefGoogle ScholarPubMed
12Martarelli, D, Martarelli, B & Pompei, P (2008) Body composition obtained from the body mass index: an Italian study. Eur J Nutr 47, 409–416.CrossRefGoogle ScholarPubMed
13Duggleby, SL, Jackson, AA, Godfrey, KM, et al. (2009) Cut-off points for anthropometric indices of adiposity: differential classification in a large population of young women. Br J Nutr 101, 424–430.CrossRefGoogle Scholar
14Carlin, BP & Louis, TA (2000) Bayes and empirical Bayes methods for data analysis. In Texts in Statistical Science, p. 419. Boca Raton, FL: Chapman & Hall/CRC.Google Scholar
15Albert, I, Grenier, E, Denis, JB, et al. (2008) Quantitative risk assessment from farm to fork and beyond: a global Bayesian approach concerning food-borne diseases. Risk Anal 28, 557–571.CrossRefGoogle ScholarPubMed
16Pouillot, R, Albert, I, Cornu, M, et al. (2003) Estimation of uncertainty and variability in bacterial growth using Bayesian inference. Application to Listeria monocytogenes. Int J Food Microbiol 81, 87–104.CrossRefGoogle ScholarPubMed
17Jeanpierre, L & Charpillet, F (2004) Automated medical diagnosis with fuzzy stochastic models: monitoring chronic diseases. Acta Biotheor 52, 291–311.CrossRefGoogle ScholarPubMed
18Ellis, KJ (2000) Human body composition: in vivo methods. Physiol Rev 80, 649–680.CrossRefGoogle ScholarPubMed
19Piers, LS, Rowley, KG, Soares, MJ, et al. (2003) Relation of adiposity and body fat distribution to body mass index in Australians of Aboriginal and European ancestry. Eur J Clin Nutr 57, 956–963.CrossRefGoogle ScholarPubMed
20Deurenberg, P (2001) Universal cut-off BMI points for obesity are not appropriate. Br J Nutr 85, 135–136.CrossRefGoogle Scholar
21Jackson, AS, Ellis, KJ, McFarlin, BK, et al. (2009) Body mass index bias in defining obesity of diverse young adults: the Training Intervention and Genetics of Exercise Response (TIGER) study. Br J Nutr 102, 1084–1090.CrossRefGoogle ScholarPubMed
22Jackson, AS, Stanforth, PR, Gagnon, J, et al. (2002) The effect of sex, age and race on estimating percentage body fat from body mass index: The Heritage Family Study. Int J Obes Relat Metab Disord 26, 789–796.CrossRefGoogle ScholarPubMed
23Schoeller, D, Tylavsky, F, Baer, DJ, et al. (2005) QDR 4500A dual-energy X-ray absorptiometer underestimates fat mass in comparison with criterion methods in adults. Am J Clin Nutr 81, 1018–1025.CrossRefGoogle ScholarPubMed
24Denis, JB, Delignette-Müller, M-L & Pouillot, R (2009) The Rebastaba project.http://w3.jouy.inra.fr/unites/miaj/public/matrisq/jbdenis/outils/welcome.html.Google Scholar
25Heymsfield, SB, Lohman, TG, Wang, Z, et al. (2005) Human Body Composition. Champaign, IL: Human Kinetics.CrossRefGoogle Scholar
26Larsson, I, Henning, B, Lindroos, AK, et al. (2006) Optimized predictions of absolute and relative amounts of body fat from weight, height, other anthropometric predictors, and age 1. Am J Clin Nutr 83, 252–259.CrossRefGoogle ScholarPubMed
27Gasperino, JA, Wang, J, Pierson, RN, et al. (1995) Age-related changes in musculoskeletal mass between black and white women. Metabolism 44, 30–34.CrossRefGoogle ScholarPubMed
28Aloia, JF, Vaswani, A, Feuerman, M, et al. (2000) Differences in skeletal and muscle mass with aging in black and white women. Am J Physiol Endocrinol Metab 278, E1153–E1157.CrossRefGoogle ScholarPubMed
29Lear, SA, Humphries, KH, Kohli, S, et al. (2007) Visceral adipose tissue accumulation differs according to ethnic background: results of the Multicultural Community Health Assessment Trial (M-CHAT). Am J Clin Nutr 86, 353–359.CrossRefGoogle ScholarPubMed
30Kagawa, M, Kerr, D, Uchida, H, et al. (2006) Differences in the relationship between BMI and percentage body fat between Japanese and Australian–Caucasian young men. Br J Nutr 95, 1002–1007.CrossRefGoogle ScholarPubMed
31Flegal, KM, Shepherd, JA, Looker, AC, et al. (2009) Comparisons of percentage body fat, body mass index, waist circumference, and waist–stature ratio in adults. Am J Clin Nutr 89, 500–508.CrossRefGoogle ScholarPubMed
32Kushner, RF (1992) Bioelectrical impedance analysis: a review of principles and applications. J Am Coll Nutr 11, 199–209.CrossRefGoogle Scholar
33Boardley, D & Pobocik, RS (2009) Obesity on the rise. Prim Care 36, 243–255.CrossRefGoogle ScholarPubMed
Figure 0

Table 1 Population description in the databases used as the reference (National Health and Nutrition Examination Survey (NHANES)), for model adjustment (CHU-fit) and for validation (CHU-valid)(Mean values and standard deviations)

Figure 1

Fig. 1 Variation of the standard error of prediction (SEP) over the tested combinations of parameters: (a) when varying the maximal distance (Dm) used in the Bayesian network prediction (arbitrary units) and (b) its covariation with the rate of prediction.

Figure 2

Table 2 Population description for the CHU-valid subjects (n 760) and the National Health and Nutrition Examination Survey (NHANES) subjects used as predictors (n 760)*(Mean values and standard deviations)

Figure 3

Fig. 2 Scatter plots of Bayesian network prediction for fat-free mass (FFM) (a), fat mass (FM) (b) and the percentage of FM (FM%) (c) in terms of their experimental counterparts derived from dual-energy X-ray absorptiometry measurements on CHU-valid men (●) and women ( × ). The first bisectors are drawn (- - -).

Figure 4

Table 3 Quality of fit between fat-free mass (FFM) and the percentage of fat mass (FM%) as measured by dual-energy X-ray absorptiometry with the CHU-valid subjects and their counterparts predicted by the Bayesian network (BN), equation 1(22) and equation 2(11) for men and women*

Figure 5

Fig. 3 Relationship between BMI and fat mass (FM), expressed as a percentage of body weight (FM%) measured by (a) dual-energy X-ray absorptiometry on CHU-valid men (●) and women ( × ) and the corresponding predictions for (b) the Bayesian network, (c) equation 1(22) and (d) equation 2(11). CHU, Clermont-Ferrand University Hospital Centre.