Article contents
Thomas Simpson and ‘Newton's method of approximation’: an enduring myth
Published online by Cambridge University Press: 05 January 2009
Extract
A resurgence of interest has occurred in ‘Newton's method of approximation’ for deriving the roots of equations, as its repetitive and mechanical character permits ready computer use. If x = α is an approximate root of the equation f(x) = 0, then the method will in most cases give a better approximation as
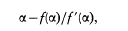
where f′(x) is the derivative of the function into which α has been substituted. Older books sometimes called it ‘the Newton–Raphson method’, although the method was invented essentially in the above form by Thomas Simpson, who published his account of the method in 1740. However, as if through a time-warp, this invention has migrated back in time and is now matter-of-factly placed by historians in Newton's De analysi of 1669. This paper will describe the steps of this curious historical transposition, and speculate as to its cause.
- Type
- Research Article
- Information
- The British Journal for the History of Science , Volume 25 , Issue 3 , September 1992 , pp. 347 - 354
- Copyright
- Copyright © British Society for the History of Science 1992
References
1 Peitgen, H. and Richter, P., The Beauty of Fractals, Berlin, 1986, 18.CrossRefGoogle Scholar
2 See e.g. Tranter, C. and Lambe, C., Advanced Level Mathematics, 4th edn, London, 1980, 302.Google Scholar
3 Simpson, T., Essays … on Mathematics, London, 1740, 81.Google Scholar
4 Pepper, J., ‘Newton's mathematical work’, in Let Newton Be! (ed. Fauvel, J. et al. ), Oxford, 1988, 63–80Google Scholar: ‘Newton made a major breakthrough [in De analysi] by introducing what is now known as the Newton–Raphson method’ (p. 73)Google Scholar. Goldstine, H., A History of Numerical Analysis from the Sixteenth Century through the Nineteenth, Springer-Verlag, New York, 1977, 64–7Google Scholar. Burton, D. M., The History of Mathematics, an Introduction, 1986, 408.Google Scholar
5 Newton, I., De analysi (ed. Jones, W.), London, 1711Google Scholar; The Mathematical Papers of Isaac Newton (ed. Whiteside, D. T.), Cambridge, 1968, ii, 206–47Google Scholar. see 218–19.
6 Newton, I., De methodis fluxionum et serierum infinitorum’, London, 1736 (English translation Colson, J.)Google Scholar, Whiteside, , op. cit. (5), iii, 32–353Google Scholar; see 43–7, ‘The reduction of affected equations’.
7 Raphson, J., Analysis aequationum universalis…, London, 1690.Google Scholar
8 Whiteside, , op. cit. (5), ii, 218.Google Scholar
9 Wallis, J., A Treatise of Algebra both Historical and Practical, London, 1685, 338.Google Scholar
10 Frend, W., The Principles of Algebra, London, 1796, 456.Google Scholar
11 Journal Book of the Royal Society of London, 30 07 1690.Google Scholar
12 Raphson, , op. cit. (7)Google Scholar, Preface. Goldstine said of this 1690 work, ‘Here Raphson acknowledges Newton as the source of the procedure’ (Goldstine, , op. cit. (4), 64)Google Scholar. That is not the view here taken.
Thomas Simpson and ‘Newton's method of approximation’
13 Raphson, , op. cit. (7), 1–2.Google Scholar
14 Wallis, J., Opera Mathematica, ii, London, 1693, 391–6.Google Scholar
15 For a different view see Bos, H., ‘Newton, Leibniz and the Leibnizian tradition’ in From Calculus to Set Theory 1630–1910 (ed. Grattan-Guinness, I.), London, 1980, Ch. 2, 49–93, on 88.Google Scholar
16 de Moivre, A., ‘Doctrinae fluxionum …’, Philosophical Transactions (1695), 19, 52–7CrossRefGoogle Scholar. See Cajori, F., Conceptions of Limits and Fluxions in Great Britain from Newton to Woodhouse, 1919, Chicago and London, 39.CrossRefGoogle Scholar
17 Halley, E., ‘Methodus nova accurata et facilis inveniendi radices aequationum …’, Philosophical Transactions (1694), 18, 136–48.CrossRefGoogle Scholar
18 de Lagny, T. F., Méthodes nouvelles et abrégeés pour l'extraction et l'approximation des racines, Paris, 1734.Google Scholar
19 Raphson, J., A Mathematical Dictionary, London, 1702.Google Scholar
20 Simpson, T., Essays … on Mathematics, 1740, Preface, vii.Google Scholar
21 Ibid., 83–6.
22 Ibid., vii.
23 Frend, W., op. cit. (10), 456, 492.Google Scholar
24 Maseres, F., ‘On Mr Raphson's Method of Resolving Affected Equations by Approximation’, in Bernoulli's Mathematical Tracts, 1795, published by F. Maseres, London, 577–86, on 585.Google Scholar
25 Lagrange, J. L., Note V, ‘Sur la méthode d'approximation donnée par Newton’, in Traité de la résolution des équations numériques, 1st edn, Paris, 1798Google Scholar; 2nd edn, 1808, reprinted 1826, 122.
26 Grattan-Guinness, , op. cit. (15), Ch. 3, IGoogle Scholar. Grattan-Guinness, , ‘The emergence of mathematical analysis and its foundational progress, 1780–1880’, p. 115.Google Scholar
27 Lagrange, , op. cit. (25), 130–52.Google Scholar
28 Fourier, J. B. J., Analyse des équations déterminées, Paris, 1831, 169, 173 and 177.Google Scholar
29 Burnside, W. S. and Panton, A. W., The Theory of Equations, London, 1881, Note B, 384–6.Google Scholar
30 Runge, C., ‘Separation und Approximation der Wurzeln’, Encyk. der Math. Wissenschaften, 1900, 1, 404–48Google Scholar, article IB3a (pp. 433–5).
31 Cantor, M., Geschichte der Mathematik, Leipzig, 1898, iii, 114–15Google Scholar; also 2nd edn (1901), 119–20.
32 Cajori, F., ‘Historical note on the Newton–Raphson method of approximation’, American Mathematical Monthly (1911), 18, 29–32, on 30.CrossRefGoogle Scholar
33 Ibid., 31.
34 Thomas, D. J., ‘Joseph Raphson, F.R.S.’, Notes Rec. Roy. Soc. London (1990), 44, 151–67, on 155CrossRefGoogle Scholar. Thomas here mistakenly claims (p. 155) that Newton ‘never published his version’ [of approximation method], but see note 6 above. In addition the text of De analysi was reprinted in the Commercium epistolicum of 1713.
35 Boyer, C., A History of Mathematics, Princeton, 1968Google Scholar, reprinted 1980, 449.
36 Hollingdale, S., Makers of Mathematics, London, 1989, 179.Google Scholar
37 Wallis, J., op. cit. (14), 390.Google Scholar
38 The Correspondence of Isaac Newton, London, 1961, iii, 222–8.Google Scholar
39 Whiteside, D. T., ‘The mathematical principles underlying Newton's Principia’, Journal for the History of Astronomy (1790), 1, 116–38, on 119.CrossRefGoogle Scholar
40 Hall, A. R., Philosophers at War, Cambridge, 1980, 94–6.CrossRefGoogle Scholar
41 Whiteside, D. T., ‘Essay review of The Correspondence of Isaac Newton, Vol. III’, History of Science (1962), 1, 97.Google Scholar
42 Whiteside, , op. cit. (39), 119.Google Scholar
- 27
- Cited by


