1. Introduction
1.1. Models Behaving Badly
In our digital society, financial decisions rely increasingly on computer models, so when things go wrong, those models are potential blame candidates.
In some cases, there is unambiguously a human blunder (or in more sinister cases, human manipulation). For example, a spreadsheet reference may link to the wrong cell; formulas that should update are replaced by hard-coded numbers; or rows are omitted from a spreadsheet sum that should have been included. We have tabulated some of these examples below.

Model errors are not always so clear-cut. More often, modellers may adopt approaches that seemed reasonable at the time, even if with hindsight other approaches would be better. Model calibration may assume that the future is like the past, but, following a large loss, it becomes clear that other parameter values would better capture the range of outcomes. We show some examples below.

Finally, some model errors can occur even if a model is correctly specified and coded, if assumed approximations or algorithms break down. We state some examples below.

These are all examples of model risk events, and, we propose, all events that could have been prevented or at least significantly mitigated, by applying the principles of sound model risk management described in this paper.
In the actuarial world, we use models more than in nearly any other industry, so we are particularly exposed to model risk. And as with the use of models in any field, our desire and need to use them is greatest when the future is not going to be just like the past – yet this is the riskiest of situations, in which the trustworthiness of the model will be most in doubt.
In the remainder of this section, we briefly discuss the use of models in the financial world and the definition of model risk used in this report, along with its limitations.
In section 2, a comprehensive Model Risk Management Framework is proposed, addressing issues such as model risk governance and controls, model risk appetite and model risk identification. These ideas are illustrated by discussing high-profile case studies where model risk has led to substantial financial losses.
In section 3, we explore cultural aspects of model risk, by identifying the different ways in which models are (not) used in practice and the different types of model risk each of those generates. We associate this discussion with the Cultural Theory of risk, originating in anthropology and draw implications for model governance.
In section 4, we provide a detailed discussion of the mechanisms that induce the financial impact of model risk. The challenges of quantifying such a financial impact are demonstrated by case studies of life insurance proxy models, longevity risk models, and models used in financial advice; and we also consider the application to models in broader fields such as environmental models.
Overall, conclusions from the report are set out in section 5.
1.2. What are Models and Why We Need Them
A wide array of quantitative models is used every day in the financial world, to support the operations of organisations such as insurers, banks, and regulators. They range from simple formulae to complex mathematical structures. They may be implemented in a spreadsheet or by sophisticated commercial software. In the face of such variety, what makes a model a model? In the words of the Board of Governors of the Federal Reserve System (2011):Footnote 1
“[T]he term model refers to a quantitative method, system, or approach that applies statistical, economic, financial, or mathematical theories, techniques, and assumptions to process input data into quantitative estimates. A model consists of three components: an information input component, which delivers assumptions and data to the model; a processing component, which transforms inputs into estimates; and a reporting component, which translates the estimates into useful business information”.
The use of models is dictated by the complexity of the environment that financial firms navigate, of the portfolios they construct, and of the strategies they employ. Human intuition and reasoning are not enough to deal with such complexity. For example, evaluating the impact of a change in interest rates on the value of a portfolio of life policies requires the evaluation of cashflows for individual contracts (or groups of contracts), a computationally intensive exercise. Furthermore, the very idea of the “value” of a portfolio requires a model, based on assumptions and techniques drawn from areas including statistics and financial economics. Hence, while the definition of models above may include a wide range of types of model, our attention is focussed on complex computational models, such as those used in insurance pricing or capital management. Such models generally employ Monte Carlo simulation and generate as outputs probability distributions and risk metrics for various quantities of interest.
For models to be useful, they must represent real-world relations in a simplified way. Simplification cannot be avoided, given the complexity of the relationships that make modelling necessary. But simplification is also necessary in order to focus attention on those relationships that are pertinent to the application at hand and to satisfy constraints of computational power.Footnote 2
Decision making often requires quantities that can only be obtained as outputs of a quantitative model; for example, to calculate capital requirements via a value-at-risk (VaR) principle, a probability distribution of future values of a relevant portfolio quantity (e.g. net asset position) needs to be determined. It is understood that the VaR calculated through the model is (at best) a reasonable approximation. The extent to which models can be successfully used to provide such approximations, with acceptable errors will be further discussed in section 4.
However, the (in)accuracy of a model’s outputs and predictions is not the sole determinant of its usefulness. Indicatively, models can be used for:
-
- Identifying relations and interactions between input risk factors that are not self-evident.
-
- Communicating uncertainties using a commonly understood technical language.
-
- Answering “what if” questions through sensitivity analysis.
-
- Identifying sensitivities of outputs to particular inputs, thus providing guidance on areas that warrant further investigation.
-
- Revealing inconsistencies and discrepancies in other (simpler or indeed more complex) models.
Thus, models are not only necessary for decision making, but more generally as tools for reasoning about the business environment and the organisation’s strategies.
1.3. What is Model Risk?
The definition of Model Risk adopted for the purposes of this Working Party’s Report, again follows the guidance of the Federal Reserve (2011):
“The use of models invariably presents model risk, which is the potential for adverse consequences from decisions based on incorrect or misused model outputs and reports. Model risk can lead to financial loss, poor business and strategic decision making, or damage to a bank’s reputation. Model risk occurs primarily for two reasons:
-
∙ The model may have fundamental errors and may produce inaccurate outputs when viewed against the design objective and intended business uses. […]
-
∙ The model may be used incorrectly or inappropriately”.
In the rest of this section, we discuss this definition and its link to subsequent sections of the report.
The first stated reason for the occurrence of model risk is the potential for fundamental errors producing inaccurate outputs. There are many circumstances in which such errors can occur. These may be coding errors, incorrect transcription of portfolio structure into mathematical language, inadequate approximations, use of inappropriate data, or omission of material risks.Footnote 3
Some model errors, in particular those arising from mathematical inconsistencies and implementation errors, we can aim to eliminate by rigorous validation procedures and, more broadly, a robust model risk management process as elaborated in section 2. But a model by its very definition cannot be “correct” as it cannot be identified with the system it is meant to represent: some divergence between the two has to be tolerated, as formalised by a stated model risk appetite (section 2.4). Such divergence may be termed “model error”, but it is not only an unavoidable but an essential feature of modelling: simplification is exactly what makes models useful.
What is of interest in the management of model risk is thus not model error itself, but the materiality of its consequences. Model risk is a consequence of the model’s use in the organisation; a model that is not in use does not generate model risk. The possible financial impact of model risk will depend on the very specific feature of the business use that the model is put into, for example, pricing, financial planning, hedging, or capital management. The plausible size and direction of such financial impact provides us with a measure of the materiality of model risk, in the context of a specific application – a detailed discussion of this point is given in section 4.1. Furthermore, communication of model risk materiality to the board is a key issue in the governance of model risk (section 2.8).
This leads us to the second stated source of model risk: incorrect or inappropriate use. Given the likely presence of some form of model error, there will be applications where the plausible financial impact of model error will be outside model risk-appetite limits. The use of the model in such applications would indeed be inappropriate. Furthermore, a model originally developed with a particular purpose in mind, may be misused if employed for another purpose for which it is no longer fit, as demonstrated in the case studies of section 2.10.
A complication in the determination of plausible ranges of model error – and consequently ranges of financial impact – arises in the context of quantifying uncertainty.Footnote 4 In some types of model error, such as the approximation error introduced by the use of Proxy Models in modelling life portfolios (section 4.2), quantification of its range is possible by technical arguments.Footnote 5 However, in other applications, particularly those involving statistical estimation, such quantification is fraught with problems. The randomness of variables such as asset returns and claims severities makes estimates of their statistical behaviour uncertain; in other words we can never be confident that the right distribution or parameters have been chosen.
Ignorance of such a “correct model” makes the assessment of the fitness for purpose of the model in use a non-trivial question. Techniques for addressing this issue are discussed through a case study on longevity risk in section 4.3. But we note that a quantitative analysis of model uncertainty, for example, via arguments based on statistical theory, will itself be subject to model error, albeit of a different kind. Thus, model error remains elusive and the boundary of what we consider model error and what we view as quantified uncertainty keeps moving.
This particular difficulty relates to the fundamental question of whether model risk can be managed using standard tools and frameworks in risk management. At the heart of this question lie two distinct interpretations of the nature of modelling and, thus, model risk.
-
i. Modelling may be viewed as one more business activity that leads to possible benefits and also risks. In that case, model risk is a particular form of operational risk and it can be (albeit partially and imperfectly) quantified and managed using similar frameworks to those used for other types of risk. Implicit in this view is an emphasis on models as parts of more general business processes and not as drivers of decisions.
-
ii. Alternatively, one can argue that model risk is fundamentally different in nature to other risks. Model risk is pervasive: how can you manage the risk that the very tools you use to manage risk are flawed? Model risk is elusive: how can you quantify model risk without a second-order “model of model risk”, which may itself be wrong? The emphasis in this view is on the difficulties of representing the world with models. Implicit in such emphasis is the assumption that a correct answer to important questions asked in the business exists, which model uncertainty does not allow us to reach.
The reality lies between these two ends of the spectrum. Whilst there are aspects of standard operational risk management that can be applied to managing model risk, there are also important nuances to model risk that make it unique. In section 2, we therefore explain how current thinking, tools, and best practices in risk management can be leveraged and tailored to effectively manage model risk. In section 4, we then explore further the specific nuances and challenges around the quantification of model risk, where an explicit link between models and decisions is necessary in order to explore the financial implications of model risk.
The presence of uncertainties that cannot be resolved by scientific elaboration implies that differing views of a model’s accuracy and acceptable use can legitimately co-exist inside an organisation. Ways of using models differ not only in their relation to particular applications, but also in relation to the overall modelling cultures prevalent within the organisation. In some circumstances, model outputs mechanically drive decisions; in others the model provides one source of management information (MI) among many; in some contexts, the model outputs may be completely overridden by expert judgement. Different applications and circumstances may justify different approaches to model use and generate different sorts of (non-)model risks. In the presence of deep uncertainties, a variety of perceptions of the legitimate use of models is helpful for model risk management, as is further explored in section 3.
Finally, we note that the focus of this report is on technical model risks, arising primarily from errors in a quantitative model leading to decisions that have adverse financial consequences. Behavioural model risks, that is, risks arising from a change in behaviour caused by extensive use of a model (e.g. overconfidence or disregard for non-modelled risks) are only briefly touched upon in section 3. Systemic model risks, arising from the coordination of market actors through use of similar models and decision processes, remain outside the scope of this report.
1.4. Summary
In this section we argued that:
-
- Model risk is a pervasive problem across industries, where complex quantitative models are used, with substantial financial impact.
-
- Model risk occurs primarily for two reasons:
-
1. The model may have fundamental errors and may produce inaccurate outputs when viewed against the design objectives and intended uses.
-
2. The model may be used incorrectly or inappropriately.
-
-
- In the context of model uncertainty, avoiding fundamental errors can be impossible and working out the appropriate use of models can be technically challenging. Therefore development and adoption of a comprehensive Model Risk Management Framework is required.
2. How Can Model Risk Be Managed?
2.1. Real-Life Case Studies
In section 1 we explained what model risk is and the sort of major consequences that model risk events have had – particularly in recent years as models have become more prominent and complex. However, models are necessary as they are crucial to sound decision making, understanding the business environment, setting strategies, etc. So it is vital therefore to properly manage model risk.
We now consider three specific case studies to provide examples of the different aspects of models and model use that can give rise to model risk events. This will help illustrate the importance and benefits that can be gained from a Model Risk Management Framework that we set out in sections 2.2–2.9. We will then revisit the case studies in section 2.10 and look at which elements of the framework were deficient or not fully present, and consider the specific improvements that could have been made.
2.1.1. Long-Term Capital Management (LTCM) hedge fund
Synopsis. LTCM is a typical example of having a sophisticated model but not understanding its mechanisms and the factors that could affect the model. See, for example, the article “Long-term capital management: it’s a short-term memory” in the New York Times (Lowenstein Reference Lowenstein2008).
Background. The hedge fund was formed in 1993 by renowned Salomon Brothers bond trader John Meriwether. Principal shareholders included the Nobel prize-winning economists Myron Scholes and Robert Merton, who were both also on the Board of Directors. Investors paid a minimum of $10 million to get into the fund which consisted of high net worth individuals and financial institutions such as banks and pensions funds.
LTCM started with just over $1 billion in initial assets and focussed on bond trading with the strategy being to take advantage of arbitrage between securities that were incorrectly priced relative to each other. This involved hedging against a fairly regular range of volatility in foreign currencies and bonds using complex models.
What happened?. The fund achieved spectacular annual returns of 42.8% in 1995 and 40.8% in 1996. This performance was achieved, moreover, after management had taken 27% off the top in fees.
As the fund grew, management felt the need to adopt a more aggressive strategy, and move into a wider range of investments. They pursued riskier opportunities, including venturing into merger arbitrage (i.e. bets on whether or not mergers would take place), and used their models to identify merger arbitrage opportunities.
As arbitrage margins are very small, the fund took on more and more leveraged positions in order to make significant profits. At one point the fund had a debt to equity ratio of 25:1 ($125 billion of debt to £4.7 billion of equity). The notional value of their derivative position was $1.25 trillion (mainly in interest rate derivatives).
Then, in 1998, a trigger event occurred, the Russian Financial Crisis, when Russia declared it was devaluing its currency and effectively defaulted on its bonds. The effects of this were felt around the world – European markets fell by around 35% and the US markets fell by around 20%.
As a result of the economic crisis, many of the Banks and Pension funds invested in LTCM moved close to collapse. As investors sold European and Japanese bonds, the impact on LTCM was devastating. In less than 1 year, the fund lost $4.4 billion of its $4.7 billion in capital through market losses and forced liquidations.
It was feared that LTCM’s failure could cause a chain reaction of catastrophic losses in the financial markets. After an initial buy-out bid was rejected, the Federal Reserve stepped in and organised a $3.6 billion bailout to avert the possibility of a collapse of the wider financial system.
2.1.2. West Coast rail franchise
Synopsis. The £9 billion West Coast Main Line rail franchise contract is a non-financial services example of a failure in model validation.
Background. Virgin had been operating the West Coast Main Line rail up to the point of the franchise renewal in 2012. Both they and First Group bid for the franchise; after assessment by the Department for Transport, the franchise was initially awarded to First Group.
What happened?. Virgin requested a judicial review of the decision, based on questions over the forecasting and risk models used by the Department for Transport. The transport secretary agreed for an independent review to be performed.
The resulting Laidlaw report (Department for Transport and Patrick McLoughlin, 2012) found that there had been technical modelling flaws with incorrect economic assumptions used. Mistakes were made in the way in which inflation and passenger numbers were taken into account and values for these two variables were understated by up to 50%.
As a result, First Group’s bid seemed more attractive, as they were much more optimistic about how passengers and revenues could grow in the future.
The Department for Transport provided guidance to the bidders, but used different assumptions to the bidders, which created inconsistencies and confusion.
Economic assumptions were only checked at a late stage, when the Department for Transport calculated the size of the risk bond to be paid by the bidder. Errors were also found to affect the risk evaluations, which were therefore incorrect, such that the risk was understated.
The review found that external advisors had spotted some of the mistakes, hence early warning signs that things were going wrong, but there was no formal escalation of these mistakes and therefore incorrect reports were circulated.
The whole fiasco led to a huge embarrassment for the Department for Transport, with taxpayers having to pay more than £50 million for their error. Questions were raised over senior management and their levels of understanding. Three senior officials were suspended as a result and Virgin continued to run the service for another 2 years.
2.1.3. JP Morgan (JPM)
Synopsis. Named the “London Whale” by the press after the size of the trades, this was a case of poor model risk management combined with broader risk management issues that led to JPM making losses of £6 billion and being fined £1 billion. See, for example, the 2013 BBC News articles “‘London Whale’ traders charged in US over $6.2bn loss” (BBC News, 2013a) and “JP Morgan makes $920m London Whale payout to regulators” (BBC News, 2013b).
Background. JPM’s Chief Investment Office (CIO) was responsible for investing excess bank deposits in a low-risk manner. In order to manage the bank’s risk, the CIO bought synthetic CDS derivatives (their synthetic credit portfolio or SCP), which were designed to hedge against big downturns in the economy.
In fact, the SCP portfolio increased more than tenfold from $4 billion in 2010 to $51 billion in 2011 and then tripled to $157 billion in early 2012.
What happened?. The SCP portfolio, whilst initially intended as a risk management tool, instead became a speculative tool and source of profit for the bank as the financial crisis ended, and again in 2011. The CIO was short-selling SCP and betting that there would be an upturn in the market.
Existing risk controls flagged these trades that were effectively ten times more risky than the agreed guidelines. This resulted in the CIO breaching five of JPM’s critical risk controls more than 330 times.
Instead of scaling back the risk, however, JPM changed the way it measured risk, by changing its VaR metric in January 2012. Unfortunately, there was an error in the spreadsheet used to measure the revised VaR, which meant the risk was understated by 50%. This error enabled traders to continue building big bets.
As they were making large trades in a relatively small market, others noticed and took opposing positions, including a number of hedge funds and even another JPM company.
In early 2012, the European sovereign debt crisis took hold and markets reversed, leading to trading losses totalling more than $6 billion.
This prompted an inquiry by the Federal Reserve, the SEC, and ultimately the FBI, which resulted in JPM having to pay fines of $1 billion. The CEO of JPM was found to have withheld information from regulators on the Bank’s daily losses, and the incident claimed the jobs of several top JPM executives.
2.2. The Model Risk Management Framework
The concept of model risk and the management of it could reasonably be viewed as less mature than for other risk types (e.g. market, credit, insurance, operational, liquidity), which appear in standard regulatory frameworks such as Solvency II. In particular, an independent industry research survey on model risk management (Chartis Research Ltd, 2014) highlighted that few firms (only 12% of those surveyed) have a comprehensive model risk management programme, although a large proportion see model risk management as a high or their highest priority. The survey also identified that there are significant organisational and structural challenges to model risk management (lack of clear ownership of and senior engagement in model risk, siloed management of model risk), and that model risk appetite and Model Risk Policy are key to the overarching process. Further, the survey explains that whilst model risk is generally seen as an operational risk, it does not fit the operational risk definitions well. We have therefore in this section aimed to develop an enterprise-wide framework for managing model risks, to be fit to address the issues experienced in the real-life case studies, and to address these specific challenges identified.
Different organisations view and categorise model risk in different ways. Although the consequences of model risk events occurring are mainly financial, some organisations may treat model risk as a subset of both financial and operational risk.
In this paper, we have used established operational risk management processes as the starting point for the management of model risk. From this, we have developed a framework for managing model risks, based on industry best practice, regulatory developments (e.g. the US Federal Reserve’s Supervisory Guidance on Model Risk Management mentioned in Chapter 1, Solvency II), good practice general risk management principles, and consideration of the specific nuances of model risk as a risk type. The proposed Model Risk Management Framework is represented diagrammatically in Figure 1.
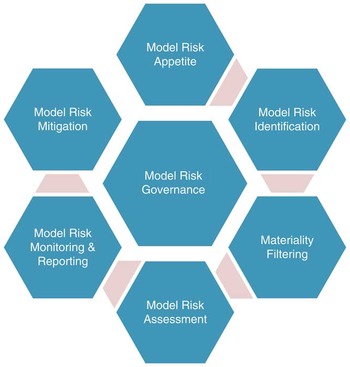
Figure 1 The Model Risk Management Framework
The terminology used may differ slightly to that used across organisations, but the concepts that are described in more detail in the following sections should be commonly understood.
For illustrative purposes the framework has been described in the language and context of a company, however, the framework is intended to be applicable more widely than this (e.g. to pension schemes, consultancies, mutual societies, regulators) so that the specific named bodies here (Board, Risk Function, etc.) can equally be replaced by the equivalent bodies or individuals in a non-corporate organisation.
We now go through each component of the Model Risk Management Framework in turn, setting out the detailed principles that we would expect a company to tailor and apply to their organisation in order to effectively manage model risk.
2.3. Model Risk Governance
We begin with governance, which is central in Figure 1 and to the Model Risk Management Framework.
In order to put in place appropriate governance around model risk, an organisation should establish an overarching Model Risk Policy, which sets out the roles and responsibilities of the various stakeholders in the model risk management process, accompanied by more detailed Modelling Standards, which set out specific requirements for the development, validation, and use of models.
2.3.1. Model Risk Policy
The Board. Overall responsibility for managing model risk must lie with the Board. This is because the consequences of model risk events can impact the financial strength of the company, as we have seen from the Introduction, and because the Board is ultimately responsible for the results and decisions of the organisation, which are built upon potentially multiple layers of models. As we will see in the section on model risk appetite, the scope and content of the model risk framework will be driven by how willing the Board is to accept the results from complex financial models.
In order to fulfil its role in managing model risk, the responsibilities of the Board could be as follows:
-
∙ specifying its appetite for model risk;
-
∙ maintaining an appropriate governance structure to ensure material models operate properly on an ongoing basis;
-
∙ ensuring there are sufficient resources available to develop, operate, and validate material models, and the appropriate skills and training are in place; and
-
∙ ensuring that all relevant personnel are aware of the procedures for the proper discharge of their responsibilities around models.
Clearly, it is important to consider proportionality and apply pragmatism in order to ensure the Board meets these responsibilities. In particular, the Board would not, in general, be expected to get involved in the detail of individual models or their associated risks (other than perhaps for regulatory capital models), however, they would be expected to define, for their key model applications (e.g. financial reporting, capital and reserving, and pricing, models) the degree of error they are willing to tolerate, as they sponsor the resources required to support that degree of tolerable error.
The Risk Function. The Board generally delegates the responsibility for day-to-day management of risks to senior management. Given that model risk is a less mature risk type and it often will not have a single owner at an enterprise level (as there are a huge number of individual models), it may be most appropriate for the Board to delegate responsibility to the Risk Function (or equivalent senior management body) to set and maintain an effective Model Risk Management Framework.
In order to fulfil its role in managing model risk, the responsibilities of the Risk Function could therefore be as follows:
-
∙ establishing and maintaining the Model Risk Management Framework;
-
∙ setting and maintaining Standards for modelling (see section 2.3.2), and monitoring compliance with these Standards;
-
∙ maintenance of the company’s aggregate model inventory (see section 2.5);
-
∙ setting and maintaining thresholds for materiality filtering (see section 2.6), and oversight of the application of these materiality thresholds;
-
∙ monitoring the company’s position against the Board’s model risk appetite (see section 2.4), and where necessary proposing relevant management actions to bring the model risk profile back into appetite (see section 2.9);
-
∙ ensuring model risk assessments are carried out (see section 2.7);
-
∙ ensuring material models and model developments are appropriately validated on a sufficiently timely and regular basis;
-
∙ identifying emerging model risks within the company; and
-
∙ model risk reporting (see section 2.8) to the Board and its delegated committee structure.
Model owners. The implementation of the Model Risk Management Framework is then the responsibility of the individuals responsible for each model, with subject matter support from the Risk Function. Therefore, for each model used in the organisation, the business must assign a model owner responsible for that model.
In order to identify who “owns” (is responsible for) each model, the company is likely to consider who developed the model. Often, however, model developers may have moved on or worked for an external party. Therefore, the individual(s) responsible for a model should be the person(s) responsible for the use of the outputs of the model. A model is fundamentally just a tool to provide information for a specific use (e.g. to feed into financial results or regulatory submissions, to determine a price for a transaction, to assess the pricing level of a product, etc.). Therefore, the individual who uses the outputs of the model to meet the responsibilities of their role, should be responsible for the model. So the onus is on the model user to “own” the model and ensure that they understand it, which will require appropriate knowledge transfer to be undertaken with the model developer. The same applies when the model user changes. To avoid key person dependencies for important models, it is sensible to ensure that more than one individual has a deep understanding of the model.
Where there are multiple users of a model, a primary owner should be allocated, responsible for ensuring the model complies with the Model Risk Management Framework. Depending on the different applications of the model in this case, it may be appropriate for the primary owner to be a more senior individual in the organisation commensurate with the materiality of the most important applications. Secondary users will still need to comply with the general requirements of the Model Risk Management Framework but can place some reliance on the primary owner, for example, for the documentation of the model and the generic expert judgements and limitations, overseeing validation, etc. However, where the secondary users make changes to the model, or any documentation, expert judgements, limitations, and model output reports are specific to their use, they will need to ensure these meet the requirements of the Framework.
As the use of models has become much more widespread, and models in organisations have become more complex, in recent years, not all model users will have the requisite technical skills to be able to fully comply with the Framework requirements or indeed maintain their models. Where this is the case where they should work with the Risk Function for support in understanding how to apply the Framework, and engage the support of the model developers, Actuarial Function, or other relevant experts for support in understanding the technical aspects of the model. However, they still retain responsibility and as a minimum should maintain an overall understanding of the model and its key underlying assumptions and limitations.
The primary responsibility of the model owner is to ensure that the model complies with the requirements of the Model Risk Management Framework. This involves capturing the model in the organisation’s model inventory, assessing it against the materiality criteria, and ensuring that the model complies with the Modelling Standards applicable to its risk rating – that is, that the model is properly developed, implemented, and used, and has undergone appropriate validation and approval. In particular, the model owner should be able to actively focus on the Standards around model use – that is, are the applications that the model is being used for appropriate, and are the outputs from the model properly understood. The model owner is also responsible for providing all necessary information for validation of the model.
Governance committee. Like any other type of risk, there needs to be formal governance around the management of model risk. There needs to be clarity over the committee structure that will oversee model risk and receive regular model risk MI reports. The precise committee structure will depend on the nature of the organisation and on the Board’s view of the relative importance of the risk. Appropriate governance could certainly be achieved through the existing committee structure; it is not necessary to introduce new committees specifically for the governance of model risk. For example, it may be more practical for a company to govern insurance pricing models in the same forum as where insurance pricing is governed, rather than to separate out the governance of models. However, it is important that there is clarity of oversight of model risk as there can be elements of cross-over between financial and operational risks (and the expertise for their management) that stem from model risk.
Once we have identified the committee responsible for oversight of model risk, we need to ensure that there is appropriate representation on the committee, and an appropriate governance process around model risk management that embraces all types of model risk cultures, in order to achieve optimal model risk management results. This is discussed further in section 3.
In order to fulfil its responsibilities around model risk management, the terms of reference of the governance committee could include the following
-
∙ Exercise governance and oversight over the development, operation, and validation of all material models used by the company, to ensure that they are fit for purpose, adequately utilised in the business, and comply with regulatory requirements.
-
∙ Monitor the model inventory for completeness and adequacy.
-
∙ Review and approve material model changes and developments.
-
∙ Review all model validation reports, approve the associated action plans to address findings, and monitor progress against agreed action plans.
-
∙ Manage model risk within the Board’s model risk appetite.
-
∙ Monitor emerging model risks within the company.
-
∙ Monitor compliance of models with the Modelling Standards, escalate breaches as appropriate, and consider the appropriateness of proposed rectification plans.
Internal audit. Internal audit is responsible for evaluating the adequacy and effectiveness of the overall system of governance around model development, operation, and validation.
2.3.2. Modelling Standards
In order to embed the Model Risk Management Framework into the running of the business, as described above the Risk Function (or equivalent) should set minimum standards that model owners and validators are expected to adhere to. This is a familiar concept for many insurers in respect of Solvency II internal models. Companies could therefore develop similar but higher level standards that would be applicable to all business material models (i.e. those models that exceed the materiality thresholds as defined in section 2.6). These standards would contain only those specific requirements that senior management expect around the modelling process in order for the Board to gain comfort over the fitness for purpose of these models. Furthermore, these Standards could be applied in a graduated or differential manner according to the materiality rating of the model. For example, models could be categorised as immaterial, low materiality, medium materiality, or high materiality through the materiality filtering process; and the Standards could then explicitly separate out the “base” requirements applicable to all material models, the additional requirements applicable to all models rated medium or higher, and the further requirements only applicable to high materiality models.
In general, the Modelling Standards should typically include requirements in the areas set out in Figure 2.

Figure 2 Modelling Standards
2.4. Model Risk Appetite
The explicit consideration of an appetite for model risk is a relatively new concept, but for effective management of any risk, the Board’s appetite for that risk needs to be defined and articulated into a risk-appetite statement. Expression of the Board’s appetite for model risk is the second vital step in model risk management, following the establishment of Policy.
Risk appetite is defined as the amount and type of risk that an organisation is willing to take in order to meet their strategic objectives. Each organisation has a different view on, or appetite for, different risks, including model risk, which will depend on their sector, culture, and objectives. Specifically in the case of model risk, the Board has to establish the extent of its willingness, or otherwise, to accept results from complex models.
Furthermore, the Board’s appetite for model risk is likely to vary depending on the purpose for which a model is being used. This should be considered when determining the materiality criteria used to assess which models are most significant for the organisation (an issue addressed below in section 2.6). By definition, the Model Risk Management Framework should be applied to those models which are most business-critical for the purposes of decision making, financial reporting, etc. Therefore, the appetite for errors in these, and hence model risk, will be the lowest.
As with any risk, the risk appetite for model risk should be articulated in the form of appetite statements or risk tolerances, translated into specific metrics with associated limits for the extent of model risk the Board is prepared to take. For example, some of the metrics that could be considered in a model risk-appetite statement are as follows:
-
∙ aggregate quantitative model risk exposure (see section 2.7);
-
∙ extent to which all models used have been identified and risk assessed;
-
∙ extent to which models are compliant with Standards applicable to their materiality rating;
-
∙ extent to which uncertainty around model outputs is transparently presented to model users;
-
∙ number of high-risk-rated models;
-
∙ cumulative amounts or numbers of model errors;
-
∙ number of models rated not fit for purpose through independent validation;
-
∙ scale or number of noted model weaknesses;
-
∙ the scale or number of model developments needed to address errors or weaknesses;
-
∙ the duration of outstanding or overdue remediation actions;
-
∙ the number of overdue validations; and
-
∙ the number or scales of model-related internal audit issues.
As mentioned in section 2.3.1, it is important to consider proportionality and apply pragmatism in the Board’s role on setting model risk appetite. For example, a short set of questions focussing on the aspects above of most relevance to the organisation and the most material model applications, can both engage the Board or relevant sub-committee and make the process simple and efficient.
The company’s position against the model risk appetite (i.e. the company’s “model risk profile”) should be monitored by the body responsible for model risk governance on a regular (e.g. quarterly) basis, and should allow management to identify whether the company is within or outside appetite.
2.5. Model Risk Identification
With the Model Risk Policy framed and the Board’s appetite for model risk established, the next step is to identify the model risks that a company is exposed to. In order to do this, it is necessary to identify all existing models, and key model changes, or new developments.
In terms of existing models, a model inventory or log should be created, in which each team or Function is required to list the models it uses. This does need to include obsolete models that are no longer used. All models across the organisation fitting the definition in section 1.2 should be considered, for example, spreadsheets used to calculate policy values, and not just those used to produce financial projections and statutory results.
In an insurance company, for example, the model inventory may include the following types of models:
-
∙ reserving;
-
∙ regulatory capital;
-
∙ EEV/MCEV;
-
∙ product pricing;
-
∙ economic capital;
-
∙ ALM;
-
∙ transaction support;
-
∙ forecasting;
-
∙ benefit illustration;
-
∙ claims values;
-
∙ experience analysis; and
-
∙ reinsurance.
It is helpful to categorise the different types of models into groupings – either by purpose/application (as above) or by process (e.g. asset valuation, liability cashflow, aggregation, etc.). This allows the organisation to build up a picture of where the model usage is and which areas run the most model risk. It may be difficult to find a categorisation that fits all models well, but it is important to agree on an approach which is practical for managing the organisation’s models. For example, where model inventories are used to identify when models are next due for validation, categorisation by purpose may be more helpful. Similarly, spreadsheets often hand-off from one to another (typical “chains” can easily comprise 50 separate spreadsheets, each run by different people and stored in different locations, etc.) so it can be helpful to group these together as a single “model” by considering the end purpose/application of these spreadsheets.
The model inventory should capture key features for each model, including but not limited to:
-
∙ the model owner;
-
∙ what the model is called;
-
∙ the name of the model platform or system;
-
∙ a brief description of what the model is used for;
-
∙ an overview of how the model works;
-
∙ the frequency of its use;
-
∙ the key assumptions or inputs;
-
∙ where on the network the model is stored;
-
∙ etc.
The inventory could also take account of any model hierarchy and dependencies, as it is common for some models to be inter-related. In its simplest form, this might just be where a group model takes the results from the models of its subsidiaries. Alternatively, it may be more complex, for example, where the results of cashflow or balance sheet models are used in further models that stress the results under a range of scenarios. This could be incorporated in a number of ways, depending on the organisation and range of models. One way to accommodate this would be to allocate each model as Level 1, 2, 3, etc. within a hierarchy and use unique reference numbers for the models to demonstrate which depend on which. For particularly complex model interdependencies, a diagram may help illustrate the links.
The information captured in the model inventory will be crucial in making the materiality assessment for each model (see section 2.6) to determine the risk rating of each model and hence the extent to which the Model Risk Management Framework needs to be applied.
Once created it is imperative that the log is maintained, because the business will evolve and new models will regularly be developed. In addition, previously non-material models can become material and vice versa.
In the same way, an organisation should create and maintain a model development log or inventory – that is, a log of the planned and in progress material model changes and developments, in order to identify risks from model changes or new model developments. The model development log should contain similar information to the model inventory, for example:
-
∙ the model purpose/application
-
∙ a brief description of the model development;
-
∙ scope of the model development;
-
∙ rationale for model development;
-
∙ the name of the model platform or system for the model development;
-
∙ current status of the model development;
-
∙ model development impact (quantitative);
-
∙ model development impact (qualitative);
-
∙ model development validation rating;
-
∙ key validation issues identified;
-
∙ key actions outstanding to complete and approve the development;
-
∙ etc.
2.6. Materiality Filtering
The model inventory and development log will likely identify a large number of models and model developments in an organisation. A materiality filter should therefore be applied (in line with the firm’s model risk appetite) to identify the models and model developments which are material (i.e. present a material risk) to the organisation as a whole, and which thus need to be more robustly managed. Materiality criteria should therefore be defined to determine which models in the model inventory and which model developments in the model development log are viewed as material, with these models then being managed in line with the Model Risk Management Framework. Furthermore, the framework and the materiality criteria could be enhanced to include graduations of thresholds – to differentiate between immaterial, low materiality, medium materiality, and high materiality models, with each category of models being subject to appropriate standards under the Framework. The remainder of this section only considers the simple case of models either being subject to the Framework requirements or not.
As discussed in section 2.4, the key determinant of which models are viewed as being subject to the Model Risk Management Framework is the organisation’s appetite for model risk. The less appetite the Board has for model risk, the more models and more model developments it should wish to see captured under the Model Risk Management Framework – hence the materiality criteria should be “tighter”/more stringent. In reality, there will be a practical limit to the number of models and developments that can be caught under the framework, depending on the resources the company is willing to invest in managing model risk (in the same way as for other risks). So there must be a balance in setting the materiality criteria to ensure the Model Risk Management Framework should apply to those models deemed most business-critical.
Such business-critical models will often be used in the quantification of financial measures. Therefore model risk materiality may be defined in terms of:
-
∙ profit;
-
∙ reserves;
-
∙ capital;
-
∙ asset valuation;
-
∙ price;
-
∙ sales;
-
∙ embedded value;
-
∙ cashflow;
-
∙ etc.
We may also want to consider the complexity of the models when determining model risk materiality. For example, a simple deterministic model with a handful of inputs and requiring just one or two assumptions, will likely be much less prone to model error than a complex stochastic asset liability projection model with a vast number of different inputs and assumptions that considers the interactions of multiple risk factors and lines of business.
Assessment of materiality based on such quantitative measures must be underpinned by a qualitative assessment, made by the relevant model owner. This qualitative assessment should encompass criteria such as:
-
∙ What is the extent of reliance on the results of the model for decision making?
-
∙ How important are the decisions being made (e.g. do they impact on the organisation’s strategic objectives)?
-
∙ How sensitive are the results to changes in parameters or assumptions?
-
∙ What is the potential for adverse customer impact due to the model results?
-
∙ etc.
To make the qualitative aspects useable in the materiality assessment, a standardised approach will be necessary to reach an overall conclusion on the qualitative aspects of materiality. This might be achieved through comparison of the model, for each of the criteria considered, against a set of descriptions, corresponding to points on a scale of materiality. The overall assessment might be then the most material outcome on any criteria considered or some (weighted) average of the results for each of the criteria.
Together, the information and data captured in the model inventory and model development log must be sufficient to enable the quantitative and qualitative materiality assessment to be made.
To illustrate the suggested approach, we have considered the example of the West Coast Main Line bid (section 2.1.2). Here, the quantitative assessment would naturally have been at the highest rating given the purpose of the model was to secure the promised multi-billion franchise payments (through quantifying the funding arrangements of the bidding entity).
From a qualitative perspective, section 2.1.2 describes heavy reliance on the model, with the output being highly relevant to the assessment of the bids (so of “strategic” importance, given the Department for Transport’s objective to re-franchise the railway). The decision also had a national impact on “customers”, given that it would affect the 26 million annual journeys made by the travelling public (as referenced in the Department for Transport’s Stakeholder Briefing Document, 2011). These factors would each have indicated a high qualitative rating.
Whether the model, as used, would have been sensitive to changes in assumptions is unclear, given the resulting problems that emerged. However, given the combination of high quantitative and qualitative ratings, a future model of this nature would be subject to the proposed Model Risk Management Framework, which would require such testing.
2.7. Model Risk Assessment
Once we have identified the models and model developments which are material, the next step is to assess the extent of model risk for each material model or model development. This should involve carrying out both a quantitative assessment, and a qualitative assessment, and considering both gross and net of controls. We can then aggregate this to derive an overall company-level model risk assessment. The process for carrying out this assessment is described in detail below.
2.7.1. Quantitative assessment for an individual model or model development
In order to quantify the model risk inherent in a model or model development, the following approach can be taken (analogous to the way any other risks would be measured):
-
1. Where there is a reasonable analytical measurement approach of estimating the financial impact of the model risk, this should be used (see section 4).
-
2. Where an analytical model risk measurement approach is not available, an “operational risk style” scenario-based approach should be taken, considering any relevant available data, to quantify the financial impact of the model risk.
To the extent possible, these assessments should be carried out using both gross and net of controls (i.e. before and after allowing for the application of the Model Risk Policy and Standards per section 2.3 in the model/model development), albeit acknowledging any allowance can only be crude/high level. For example, if we are using the scenario-based approach, then the scenario causing a loss may differ, or the frequency or severity assessments of the scenario may differ, depending on if we are applying the Policy and Standards or not.
If we consider the different ways in which model risk is generated: human blunders/errors; inappropriate use; and model uncertainty; then it is likely to be virtually impossible to derive a meaningful quantitative assessment of human blunders, it will be very challenging but may be possible at a high level to quantify the impact of inappropriate use of models, and it should be possible to derive a meaningful quantification of model uncertainty. For example, where it cannot be evidenced that software or spreadsheets have been through recognised testing protocols, then the models and output will generally be expected to be less accurate. Therefore, the quantitative assessments of model risk for individual models or model developments are most likely to relate to model uncertainty – this is covered in more detail in section 4.
2.7.2. Qualitative assessment for an individual model or model development
A qualitative assessment of the model risk should also be carried out.
On a “gross of controls” basis, the high/medium/low materiality assessment from section 2.6 could translate directly to a high/medium/low-risk assessment.
On a “net of controls” basis, we would consider the fitness for purpose of the model or model development, and depending on this we could reduce the risk rating accordingly from the “gross of controls” assessment. So, for example, if a model was assessed as high materiality but had been recently robustly validated as fit for purpose with no material open issues, the net model risk assessment may be low risk.
The fitness for purpose of a model or model development is determined by considering the effectiveness of the model or model development against each area of the Model Risk Policy and Standards (i.e. what is the quality of the data, has the model been developed subject to proper change controls, has the model been properly documented, are the key assumptions and limitations properly understood, is it being used for appropriate applications, etc.). This could be informed by the latest model validation report in respect of the model or model development; or alternatively the model risk governance body could commission the model validator to carry out the assessment, or equivalently commission the model developer to carry out the assessment and the model validator to peer review and challenge the assessment. Examples of possible diagrammatic and dashboard presentations of qualitative net of controls model risk assessments are set out in Figures 3 and 4 in section 2.8.3.

Figure 3 Diagrammatic presentation of qualitative model risk assessment

Figure 4 Dashboard presentation of qualitative model risk assessment
2.7.3. Enterprise-wide model risk assessment
In order to assess the overall model risk profile of the company, we make an assessment based on the risk assessments of the individual material models used in the organisation. Again, there will be a quantitative and a qualitative assessment.
The quantitative assessment will aggregate the individual quantitative model risk assessments, using appropriate correlation factors. Given the likely crudeness of the individual assessments, a broad-brush low positive correlation may be reasonable.
The qualitative assessment will consider the qualitative metrics in the model risk appetite – for example, the extent to which all models used have been identified and risk assessed, the extent to which models are compliant with Standards applicable to their materiality rating, the number of high-risk-rated models, cumulative amounts of model errors, etc.
2.8. Model Risk Monitoring and Reporting
Given that the Board has ultimate responsibility for managing the model risk of an organisation, it is important that the model risk MI presented to the Board and its delegated committee structure enables effective oversight of model risk.
2.8.1. Style
The MI should be set out in terms which are meaningful to the Board and relevant in the context of the Board’s objectives. Furthermore, the MI should be tailored to the cultures of the stakeholders on the Board and relevant sub-committees (this is elaborated upon in section 3).
2.8.2. Content
The model risk MI would be expected to cover the following as a minimum:
-
∙ The organisation’s overall model risk profile compared with its agreed appetite (as per section 2.4).
-
∙ Any recommended management actions to be taken where necessary to manage the company’s model risk within appetite (as per section 2.9).
-
∙ Monitoring of the material models in the model inventory in scope of the Model Risk Management Framework (as per sections 2.5 and 2.6), including materiality rating (low/medium/high), and quantitative and qualitative model risk assessments (as per section 2.7).
-
∙ Key model developments in progress or recently completed (as per section 2.5).
-
∙ Outcomes of model validations, highlighting any issues or areas of weakness.
-
∙ Actions being taken by management to address any model validation issues, weaknesses, or breaches of Modelling Standards, and progress against these actions.
-
∙ Any emerging trends or risks with model risk, whether within the organisation or from information/reports from other companies.
The MI should focus on the company’s material models, and the extent of reporting should be proportionate to the materiality of the model(s) and their use(s). The level of trust that the Board has in complex models, and the level of complexity of the organisation’s model inventory, will be key in determining the detail of reporting.
The majority of the content areas are self-explanatory or covered in the relevant subsections in this section; one aspect that merits further detail is around material model monitoring.
2.8.3. Material model monitoring
In defining model risk in section 1.3, two main generators of risk were identified – fundamental errors and incorrect or inappropriate use. The potential for errors is a more “familiar” risk for companies, and operational risk reporting MI could be the starting point for developing MI around this aspect. For example, typical operational risk MI covers the frequency and severity assessments of top operational risk events, the effectiveness of controls, and metrics such as observed losses, which would be relevant to model risk.
The risk arising from incorrect or inappropriate use of a model is however a less-familiar concept, so reporting on this risk may require a new approach to be developed. Different decision makers will take account of different pieces of information in coming to their decisions, and the emphasis on the model may vary. However, there is a danger that a decision may be made entirely based on a model’s results (our “Confident Model Users” perspective in section 3), without appreciation of the potential range of outcomes, or that information from a model is ignored in coming to a decision (which might be the style of the “Intuitive Decision Maker” or the “Uncertainty Avoider” in section 3). Therefore, the MI on model use risk should focus on the effectiveness of the model owners in communicating the extent of risk inherent in a model to the model users, and on the effectiveness of the model users in understanding, processing, and feeding this information into their decisions. For example, in order for a model owner to effectively communicate the extent of risk inherent in a model to the model users, good practice model output documentation (as per the Modelling Standards) should:
-
∙ set out the purpose(s) of the model;
-
∙ be appropriate to the expertise of the user audience;
-
∙ provide a reasonable range or confidence interval around the model result (e.g. by using sensitivities to key expert judgements);
-
∙ convey the uncertainty inherent in the qualitative aspects of the modelling process as well;
-
∙ summarise the key expert judgements and limitations underlying the model;
-
∙ describe the extent of challenge and scrutiny that the model has been through and why this is sufficient for the relevant use;
-
∙ explain how the model or model component fits into the overall modelling process (e.g. using a flowchart showing the data in-flows and out-flows); and
-
∙ use diagrams where appropriate to support the explanation of more technical/complex modelling concepts (e.g. section 4.3 sets out an example where there are two entirely differently shaped curves which produce the same point estimate mortality assumption – if the size and timing of cashflows is related to the shape of the curve, the choice of curve may have a significant financial impact).
The volume of information required to communicate model risk can be extensive, so a high level summarised approach may assist in conveying the key messages and areas of risk to model users.
For example, Figures 3 and 4 are simple illustrations of a diagram and a dashboard using an RAG (red/amber/green) rating to reflect the extent of model risk, considering impact and probability:
In order to monitor model use risk, we may therefore monitor the effectiveness with which the output documentation (or other format of communication) of material models covers each of the above good practice areas; and from Board or committee minutes we could monitor how this information has been taken into account in informing the relevant decisions.
2.9. Model Risk Mitigation
As mentioned in section 2.4, the model risk appetite should be monitored by the body responsible for model risk governance on a regular basis, and should allow management to identify whether the company is within or outside its risk appetite. If the organisation is outside its appetite then the model risk governance body should recommend relevant actions to bring the company back into its appetite within a reasonable timeframe. Possible model risk mitigation actions that the model risk governance body may recommend in order to bring the company’s risk profile back into appetite may include, for example:
-
∙ Model developments or changes should be carried out to remediate known material issues (these may have been identified by the model user, model developer, model validator, or otherwise).
-
∙ Additional validation of the model is necessary when a new model risk has emerged or an existing model risk has changed (e.g. if new information comes to light on longevity risk or if there is greater concern over pandemic risk due to a new emerging virus).
-
∙ An overlay of expert judgement should be applied to the model output to address the uncertainty inherent in the model. For example, if there is significant uncertainty in one of the underlying assumptions and hence there is a range of plausible results, then an expert judgement may be applied to identify a more appropriate result within the range of reasonable outcomes. Alternatively, the expert judgement may be an entirely independent and objective scenario assessment to complement the modelled result, or replace the use of a model altogether.
-
∙ The Modelling Standards, or the application of the Modelling Standards, should be enhanced (e.g. specific requirements in the Standards that applied only to high materiality models could be extended to apply also to medium materiality models).
-
∙ If appropriate, additional prudence may be applied in model assumptions, or explicit additional capital may be held, to reflect the risk inherent in the model. For example, additional capital may be held in line with the quantitative model risk assessment.
2.10. Case Studies
Having set out the suggested framework for managing model risk, we now consider the real-life case studies from section 2.1 and identify the areas of the Model Risk Management Framework, which were deficient or not fully present, and consider the specific improvements that could have been made, in order to bring the Framework to life.
2.10.1. LTCM hedge fund
Model Risk Management Framework assessment. The diagram considers where the risks arose for LTCM.

Model use. There was an over-reliance on the model and the assumption that it would always work the same way, even when LTCM moved away from their original investment strategy. The model was tailored to arbitrage, but not merger arbitrage. This resulted in LTCM taking on more risk than they could manage.
Model methodology and expert judgement. There was no transparency externally of either the investment strategy or the underlying model. Investors were only told that the strategy involved bond arbitrage. At the time, hedge funds were not subject to the same level of regulation as other investments, so that there was effectively no regulatory oversight of LTCM or their complicated models.
Model validation and external triggers. There was inadequate review of the model and its objectives when the trading strategy was changed (to include merger arbitrage). Insufficient consideration was given to the impact of low probability events such as systemic risk. This reinforced the need for and benefits of stress testing models for extreme events (in respect of both the underlying strategy, and in respect of the extension of modelling from fixed income arbitrage to merger arbitrage).
2.10.2. West Coast rail franchise
Model Risk Management Framework assessment. The diagram considers where the risks arose for the West Coast Main Line bid.

Data quality and Expert judgement. Mistakes were made in the inflation assumptions used, which were understated by 50%. These should have been checked for reasonableness, particularly as the Virgin bid would have been based on data that was complete and appropriate. This resulted in clear bias, as First Group assumed more optimistic values for inflation in the later phases of the franchise period.
Model validation. Clearly, the extent of the validation performed was inadequate as it did not identify the technical flaws in modelling or inconsistent assumptions found by the subsequent review. Fundamentally, the First Group model’s results did not sound reasonable. Richard Branson famously said that “he would run the service for free if their assumptions were correct”. Another validation flaw was that the Department for Transport’s models were not shared with bidders. Had all bidders used the same models (rather than each using their own different models) then this would have permitted the Department for Transport to compare the rival bids and identify any inconsistencies.
Model governance. There was a lack of understanding around the model by the stakeholders and overall insufficient transparency, governance, and oversight of the project. Roles and responsibilities for functions, committees, and boards within the Department for Transport were not clear. There were early warning signs that things were going wrong when external advisors spotted mistakes, but these were not communicated or formally escalated and incorrect reports were circulated to decision makers. Ultimately, there was lack of accountability, which resulted in the taxpayer paying the burden.
2.10.3. JPM
Model Risk Management Framework assessment. In this case, poor model risk management is not the only issue but also broader failings in risk management generally.

Model use. The CIO was supposed to be investing deposits in a low-risk manner, but their activities meant the WHOLE bank exceeded VaR limits for 4 consecutive days. Management claimed not to understand the risk model, but a number of CIO staff were on the executive committee.
Model validation and changes. When existing controls highlighted the level of risk, changes to the controls were implemented but errors meant that these understated the risk by half. The controls were adjusted to suit the (in)validity of the model, not the other way around. The broader risk management issues meant that the further increase in risk-taking was not queried. The subsequent investigations found that the spreadsheet used to calculate the revised VaR metrics was created very quickly, although JPM claimed that it had been in development for a year. An internal report by JPM, however, did identify inadequate approval and implementation of the VaR model.
Model governance and expert judgements. The internal JPM report stated that CIO judgement, execution, and escalation in Q1 2012 were poor and that CIO oversight and controls did not evolve in line with the increased risk and complexity of their activities. The subsequent Senate report said that the CIO risk dashboard was “flashing red and sounding alarms”. The regulator also came in for criticism for its oversight; this inappropriate activity by JPM was first noticed in 2008, but was not followed up.
2.11. Conclusion
The Model Risk Management Framework presents a relatively simple approach for managing model risk. Clearly, it requires a not insubstantial investment of time, particularly from the Risk Function and from model owners, to implement, however, much of what is involved is common sense and good business practice. In particular, in the modern day environment the Board and Senior Management expect that results reported to them have been properly checked and that the models used to generate them are fully understood.
We have seen from the various case studies that model risk can cause very large losses or errors, and that a well-implemented Model Risk Management Framework could potentially have averted these. In the past 10–15 years, companies have generally implemented stronger controls around regulatory and embedded value reporting models. The Model Risk Management Framework builds on this to create an enterprise-wide framework that fits all material models that an organisation uses, embraces thought leadership and best practice from recent market and regulatory developments, and applies sound risk management principles that are already embedded for more established risk types.
In summary, a Model Risk Management Framework should cover:
-
∙ The Board’s appetite for model risk and the articulation of this into a clear statement.
-
∙ The identification of model risks that the organisation is exposed to and which of these are sufficiently material to warrant more comprehensive management.
-
∙ The quantitative and qualitative assessment of these model risks.
-
∙ The monitoring of these risk assessments by the relevant governance body, which should take action, where necessary, to bring the model risk back into line with the Board’s appetite.
Of course any risk management framework can only ever be as good as the people who use it. This will depend on how well-embedded risk culture is in the organisation more generally.
3. Governance and Model Culture
3.1. Introduction
In section 2, we described a range of techniques that have been developed in recent years to manage more effectively the portfolio of models and their associated risks within an organisation. These techniques relate to the consideration of model risk as a risk to be managed as any other; the identification and ranking of models (through an inventory and model risk assessment); and the reduction of model risk through validation and change control. Furthermore, restrictions are imposed on the use of models (so that decisions are only supported by models when the models are “fit for purpose”), as well as requirements introduced for a “use test” (so that models are adapted in response to feedback from the users).
These are common features of Model Risk Management Frameworks which have been developed as a response to some of the shortcomings of models noted through the case studies described in section 2.10, including the specific issues identified during the financial crisis, such as a lack of understanding of the assumptions on which models were based and the appropriateness of such assumptions in a range of market conditions. In this, we recognise that this report is building on the shoulders of existing thinking on Model Risk Management, such as the guidance issued by the Federal Reserve (2011) and by HM Treasury (2013).
Whilst market practice has significantly advanced in recent years, as in, for example, the level of control and governance activities in respect of specific models (such as internal models under Solvency II), in many cases more still needs to be done to embed these techniques across all models used in an organisation.
Notwithstanding the scope for further embedding of Model Risk Management Frameworks, in this section we consider how to further build on such frameworks. Model risk is a consequence of the way that a model is used in decision making. Presuming that decisions are generally driven by model outputs according to uncontested principles, makes both management and quantification of model risk possible, as discussed in sections 2 and 4, respectively. Such a presumption is necessary in order to frame model risk in a tractable way.
However, we know that often decisions are not made purely based on the output of models and that different stakeholders within an organisation will tend to disagree about the ways in which models can and should be used in decision making. In this section we work towards a classification of alternative ways of (not) using models in decision making and discuss how the recognition of such distinct perspectives on modelling can enhance the practice of model risk management. In particular, building on the arguments of section 2.3 it is seen that a wide representation of stakeholders, beyond model users and developers, is necessary in model governance.
3.2. Classifying Perceptions of Appropriate Model Use
Our proposed categorisation of different attitudes to models and modelling is given in Figure 5. Each of the four quadrants depicted represents a particular attitude towards models and their uses. These are not intended as psychological profiles; rather they are generic perceptions that can be held by different stakeholders at different times, depending on their position within an organisation and the specific processes they are involved in.

Figure 5 Alternative perceptions of modelling and its uses
In this representation, the horizontal axis reflects the perceived legitimacy of modelling: in the right half-plane, it is believed that models should be used in decision making, such that the emphasis is on measurement, computation, and mathematical abstraction. In the left half-plane, models are afforded an insubstantial role in decision making – here the emphasis is on intuition and subjective belief.
The vertical axis reflects concern with uncertainty. Stakeholders in the top half-plane are confident in their processes leading to good decisions and are generally not concerned about model uncertainty. Agents in the bottom half-plane are less sure of themselves; in particular, model uncertainty is a major concern for them.
Using (or indeed not using) models in a way consistent with the perceptions of each quadrant generates different sorts of risks, as is discussed below.
3.2.1. Confident Model Users
At top-right, Confident Model Users are keen to use their models in order to take decisions that are optimal. For them, decision making is a process that can and should be driven by modelling. A sophisticated complex model that gives detailed MI and can be used extensively across the enterprise is considered desirable.
The possibility that the model may be substantially flawed is not seriously considered by such agents. Slipping into Rumsfeld-speak, their concern is with Known Knowns: the aspects of the risk environment that can be readily identified and quantified.
Such agents are likely to ignore for too long evidence discordant with their models. They will also be less concerned about whether the model being used is appropriate to the particular purpose to which it is currently being put. In this quadrant, the main risk consists of model inaccuracies driving wrong decisions. This is indeed one of the key kinds of model risk that the Model Risk Management Frameworks described so far seek to address.
3.2.2. Conscientious Modellers
At bottom-right, we find Conscientious Modellers, who are primarily concerned with the technical validity of the model in use. For such agents, fitting a traditional actuarial perspective, technical expertise, and professionalism are of paramount importance. Fitness for purpose of models is the primary focus. Conscientious Modellers are likely to conduct model validation and attempt to quantify model uncertainty. They like to repeat that “all models are wrong” – but they believe that they have the technical tools to identify the materiality of possible model errors, via an assortment of techniques such as sensitivity analysis and the methods that will be discussed in section 4, such that application of the model in an area where it will not perform reliably can be avoided. Conscientious modelling is typically the kind of behaviour that modern regulations encourage as good practice.
The concern of Conscientious Modellers thus is with Known Unknowns, those uncertainties that can be identified and managed, using a model with carefully delimited scope.
However, the emphasis of Conscientious Modellers on refining models and limiting their scope of application may lead to delays in the release of models and to obstacles to using models to derive business benefits. The technical focus of such agents may attenuate their appreciation of the operational needs that models must address and of the commercial implications of (technically equally plausible) model parameterisations.
Furthermore, despite their best endeavours, it will sometimes be the case that the overall scientific paradigm that Conscientious Modellers use in their modelling – no matter how necessary for their deliberations – is flawed. This is unavoidable, as in order to support the sophisticated mathematical structures of a quantitative risk model, a number of implicit assumptions are necessary. Examples include linear valuation functionals (not true in the midst of a liquidity crisis, but a fundamental building block of financial engineering) or stationarity of claims severities (almost never true, but a necessary simplification for distribution fitting.)
3.2.3. Uncertainty Avoiders
Uncertainty Avoiders populate the bottom-left corner of Figure 5. In their view, all risks that matter are ever-changing and interconnected. Paradigms constantly shift and modellers are like the proverbial “general fighting the last war”. Uncertainty Avoiders are highly concerned with model uncertainty, to the extent that they do not think that models used to quantify risk mathematically can ever be “fit for purpose”. They have a clear preference towards stress and scenario testing, drawing from their experience to envision novel scenarios that could lead to catastrophic losses.
The concern of Uncertainty Avoiders is with Unknown Unknowns, the risks that are bound to defy our expectations and elude quantification.
Uncertainty Avoiders believe that decisions should be robust to model uncertainty. However, such decisions will by necessity be highly suboptimal, implying a preference for mitigating, transferring, and diversifying risk. Thus, the position of Uncertainty Avoiders can become difficult in an organisation focussed on delivering profit, as they will tend to raise challenges in areas requiring decisions. However, Uncertainty Avoiders may find a supported role in, say, an emerging risks committee. They can be effective at providing “big picture” or fundamental challenge to the decision-making approach (whether based on modelling or intuition) by questioning the modelling paradigm, rationale, or evidence for the approach followed.
3.2.4. Intuitive Decision Makers
Finally, Intuitive Decision Makers do not see why models should be used in the first place. For them, gut instinct and deep knowledge of market realities will always trump mathematical abstraction. Intuitive Decision Makers doubt the relevance of model outputs to the real-world decisions they have to make. At best models are an irrelevance to them, at worst they are an unwelcome constraint on their ability to act.
Whether a model is correct or not is an issue of no consequence for Intuitive Decision Makers. Their lack of concern for models and model uncertainty generates Unknown Knowns, the possibly knowable facets of risk that are wilfully ignored (Gray, Reference Gray2014).
The immediate risk with such an attitude arises from ignoring the information and insight that a model can bring; human intuition cannot always cope with the full complexity of the problems that we often have to tackle.
Intuitive Decision Makers may, nevertheless, feel compelled to demonstrate the use of a model (by perceptions of best practice or by regulatory stricture). Then they will show strong preference towards a model whose results align with their views and corroborate their position. Modellers may be given incentives to cherry pick across plausible models in order to generate the “right results” or manipulate the model methodology/assumption setting to get convenient answers. In this scenario, the major risk is loss of accountability: if intuition fails, will it be recognised as such – or will models (and modellers) take the blame?
3.2.5. No consensus
Different quadrants in the above classification will imply different, not readily compatible, responses to model uncertainty. For example, in the longevity example that will be discussed in section 4.3 substantial model uncertainty exists – many quite differently structured, alternative, candidate models are plausible and equally fit for purpose – such that models leading to very different outputs are all consistent with observed data. Then, one can imagine Conscientious Modellers considering the outputs of a wide range of models and examining the sensitivity of the output to model choice (e.g. via the Fisher information and multiple model approaches that will be further discussed in section 4.3). Uncertainty Avoiders would be more inclined to consider the impact of scenarios, such as a future government successfully tackling obesity and other health problems associated with the consumption of processed food, in order to work out the possible exposure to longevity risk. Confident Model Users would be less inclined to follow such deliberations – a single model, one that fits the data well and easily useable in internal processes such as pricing, will be chosen. Finally, Intuitive Decision Makers will be tempted to back-solve for the model that gives outputs that “feel right” to them.
There is a legitimate argument to be made in favour of all those approaches, incompatible as they may be. When uncertainties are deep and stakes are high, all four attitudes have something useful to contribute. This is not to say that all these approaches are appropriate in all contexts. Some perspectives are clearly more appropriate than others in relation to different types of models, applications, and market conditions.Footnote 6 For example, one may well justify a Confident Model Users’ attitude when pricing personal lines policies, whereas an Uncertainty Avoider’s view is certainly valuable in the management of emerging risks. However, market conditions change and modelling tasks mutate over time: the attitude that may be appropriate now may not be so tomorrow. Maintaining multi-directional challenge in model risk governance, as discussed in section 3.4, prevents complacency and makes the enterprise more adaptable.
But acknowledging such arguments does not clarify how models should actually be used in decision making. Furthermore, it is not hard to imagine that agents subscribing to different beliefs about models as described above may have irreconcilable disagreements with each other and even fundamental objections about the way that their counterparts operate. For example, some Conscientious Modellers may view other agents as follows:
-
- Confident Model Users may be seen as naïve, not taking into account the limitations of models in decision making.
-
- Uncertainty Avoiders may be seen as unhelpful, focussed on proving inadequacies of the modelling paradigm without offering a credible alternative.
-
- Intuitive Decision Makers may be seen as cynical, with their rejection or manipulation of models threatening the professional status and integrity of Conscientious Modellers.
Of course, such ill feeling can be reciprocated – Conscientious Modellers may also be negatively perceived by other agents, for example:
-
- Confident Model Users may see them as obstructive, not allowing the model to be used in full in order to derive business benefit and a return on the investment in modelling.
-
- Uncertainty Avoiders may see them as short-sighted, focussing on “tame” quantifiable uncertainties, thus missing the big picture.
-
- Intuitive Decision Makers may see them as self-indulgent, spending time and money on esoteric investigations of little consequence for the business.
Such disagreements mean that it will generally be difficult to construct a consensus within an organisation about how models should be used and how model risk should be managed. At the same time we believe that each of the four different perspectives has a legitimate point to make and should thus have a role in model governance.
3.3. Cultural Theory
Before indicating how fundamental disagreements can be harnessed to enable a constructive dialogue, we carry out a brief excursion into the Cultural Theory of risk, a body of work originally developed in anthropology and political science, which informs much of the argumentation in this section. For an overview of the theory’s applications see Verweij & Thompson (Reference Verweij and Thompson2011). A specific application to the study of risk cultures in insurance is given by Ingram et al. (Reference Ingram, Tayler and Thompson2012). We do not review the theory here but only state some salient features:
-
1. In the presence of deep uncertainties that cannot be resolved by scientific modelling, risks are socially constructed: what we consider to be risky or otherwise depends on considerations that are primarily moral and political.
-
2. There is a finite number (four) of fundamental ways (rationalities or risk cultures Footnote 7 ) of perceiving risk, intricately linked with different ways of organising social and economic relations, different perceptions of fairness, and different strategies of information rejection.
-
3. Each of those risk cultures represents a distinct form of human wisdom. But they are also mutually incompatible, akin to people arguing from different premises. An easy consensus is thus not possible.
-
4. An institution committed to only one of these risk cultures is not viable. To facilitate viability, all four perspectives need to be represented and have genuine access to the decision-making process, which is responsive to their concerns. But given the impossibility of reaching consensus, any genuinely pluralist decision process will need to be clumsy (with all four rationalities represented, notwithstanding fundamental disagreements); strategies that are both viable and elegant (achieving coherence by being based on one rationality) are not attainable.
-
- In the context of model risk we find that each of the four rationalities of cultural theory maps onto a particular way of perceiving and (not) using models. To demonstrate this, in Figure 6, a sketch representing the myth of nature corresponding to each rationality is plotted in the respective quadrant. In each sketch, the surface and ball together represent a conception of stability–instability about the behaviour of a system; in each quadrant, therefore, stable (unstable) behaviour will result from disturbance to the ball, which disturbances may be of varying amplitudes. In the context of model uncertainty, movement of the ball on the surface in response to various disturbances over time tells us something about the emergence of new empirical evidence, hence the scope for learning (and changing one’s behaviour). Nature Benign (Confident Model Users): following any perturbation (no matter how large) the system soon returns to equilibrium. New evidence will generally confirm correctness of the model – deviations between the model and evidence are temporary effects of statistical noise.
-
- Nature Perverse/Tolerant (Conscientious Modellers): here, affairs are similar to those for Confident Model Users, but it is accepted that there are scenarios (with their associated disturbances) where existing controls will fail (events will strike the ball too forcefully) and the model will prove inadequate. Learning from failure (which is not admitted in the Confident Model Users’ view of the world) can readily occur. Uncertainty will mean that substantial revisions and refinements of the model are continuously called for. But there are model applications and operating ranges where the impact of model error is expected to be modest and therefore boundaries on model use/application must be imposed by technical experts. In other words, business performance can be generally contained between the two peaks of the surface-ball icon in this bottom-right quadrant of Figure 6.
-
- Nature Ephemeral (Uncertainty Avoiders): significant loss events will happen, unless immediate action is taken. Once these events take place, it will be clearly seen that the model used was wrong all along and that mistrust of technical expertise was justified. New evidence will always show up the inadequacy of the model.
-
- Nature Capricious (Intuitive Decision Makers): risk follows no predictable pattern, such that management cannot do much more than shed undesirable risks and cash in short-term profits, when such opportunity arises. A model should not be used in the first place, as management knows best anyway. The emergence of new empirical evidence does not change this. The ball on the “flatland” in the upper left quadrant of Figure 6 can be knocked about in any direction of travel, with seemingly no rhyme or reason. Nothing is to be learned from the ball’s “exploration” of the surface, that is, from the use of a model.
-

Figure 6 Perceptions of models for and myths of nature
An institution where all four rationalities are represented and have access to the decision-making process has a variety of strategies at its disposal and is more alert and adaptable to changes in the risk environment. Although all rationalities have a point, the strategies that each suggests may be more or less appropriate depending on the specific business application or configuration of external factors. An institution where only one of the four rationalities is represented will eventually fail, as the blind-spots that adherence to a single rationality generates will make it unable to adapt to a changing environment.
3.4. Enhancing Existing Model Risk Governance and Controls
3.4.1. Complementary perspectives
To accommodate the diverging perspectives of stakeholders in model governance, their complementarity needs to be communicated. In fact, consistently with the arguments of Cultural Theory, each way of perceiving and using models is not viable without the others. Focussing once more on Conscientious Modellers:
-
- Conscientious Modellers need the operational focus of Confident Model Users in order to raise necessary investment in the model. To attract such investment, the models produced must be user-friendly and delivered on time – endless refinement is not an option. Moreover, it has to be accepted that models will sometimes be used even if there are doubts about their accuracy, for want of a better alternative. Conversely, Confident Model Users need Conscientious Modellers in order not to use models in applications for which they are clearly ill-suited and to provide necessary refinements.
-
- Conscientious Modellers need the imagination of Uncertainty Avoiders, for the big picture challenge that they can offer and the generation of scenarios that can be used in model validation. Conversely, Uncertainty Avoiders need Conscientious Modellers to provide a structure that can be challenged – Conscientious Modellers provide the “box” that Uncertainty Avoiders like to see themselves as thinking outside of.
-
- Conscientious Modellers need the survival instinct of Intuitive Decision Makers in order to generate models that produce outputs that are consistent with market knowledge and commercially meaningful. Their input could be useful when a model might be missing an important risk driver. Equally, when an impasse exists in the decision-making process, Intuitive Decision Makers may cut through lengthy debate and allow the business to move forward. Conversely, Intuitive Decision Makers need Conscientious Modellers, as the latter can use the model to challenge management, by demonstrating “what you have to believe” (no matter how unpalatable for the Intuitive Decision Makers) for the model to be consistent with intuition. Such a challenge reveals management’s implicit assumptions and enhances accountability.
These arguments are summarised in Figure 7.

Figure 7 What Conscientious Modellers need from (left panel) and what they offer to (right panel) agents with different perspectives on modelling
3.4.2. Beyond current best practice
In our experience, current governance and controls to manage model risk often do not consider the different perspectives on the model that can exist in an organisation. Enhancements to existing controls are described below and aim to build upon such existing practices rather than replace them.
Such enhancements extend beyond the narrower regulatory perspectives that have been one of the main drivers for current approaches to model risk management. For example, the Federal Reserve’s (2011) guidance on model risk management warns against inappropriate use of models and emphasises the need to understand limitations and assumptions. It particularly advises limiting the use of models that display high sensitivity to assumptions that cannot be validated. The authors of “The dog and the frisbee” (Haldane & Madouros, Reference Haldane and Madouros2012) go further, arguing that the complexity of financial risk requires simple and robust metrics, rather than elaborate models. These two perspectives can be construed as encoding a criticism of Confident Model Users from the perspective of Conscientious Modellers (Federal Reserve) and Uncertainty Avoiders (“The dog and the frisbee”).
Our analysis indicates that in addition to those challenges, it is necessary to focus on the interactions between all holders of the four perspectives that we previously identified and to accept that the critique that each perspective directs towards the other three has some legitimacy. That such challenges take place should not be just confirmed through a box ticking exercise; instead the focus should be on improving the openness of the dialogue and the ability to raise challenges between these different groups. Indeed, HM Treasury (2013) drives in this direction.
Governance should encourage, and where necessary require, that holders of different perspectives all contribute as part of the decision-making process. Specific perspectives may be dominant in the senior ranks of organisations; in such circumstances, governance processes that, for example, require that the other viewpoints are explicitly considered and responded to may raise the profile and effectiveness of challenge that could otherwise be suppressed. The typology of Figure 5 highlights exactly which are the types of views that need to be represented.
An enhanced approach to managing model risk, reflecting potential challenges from different perspectives, might include the following:
-
- Challenging model developments at a design phase so they are sufficiently focussed on the business issues rather than in areas where the need for a more refined model is less pressing.
-
- Acceptance that model output may be highly uncertain. Therefore the model governance process may involve:
-
° Requiring that the uncertainty be explored through stress/scenario testing.
-
° Recognising that decisions still need to be made, with emphasis on assessment of issues rather than resolution or mitigation (which may be impossible).
-
° Limiting the time that can be spent by Conscientious Modellers on determining their preferred model calibration.
-
-
- Careful composition of governance committees: in such committees, a range of departments and rationalities should be represented, reflecting risk-specialist, technical, operational, and commercial perspectives.
-
- Identifying individuals aligned to each of the four areas noted above and ensuring that, to the extent possible, over-representation of one group to the exclusion of others is avoided.
-
- Embedding challenge within decision making; irrespective of whether decisions are based on model output or on intuition, already a prominent part of the Federal Reserve and HM Treasury’s guidance. Particularly, challenge originating in all four perspectives should be explicitly formulated and addressed in MI.
-
- Requiring the basis for decisions to be explicitly stated:
-
° For example, this might extend to statements of “what you have to believe” for the decision to be valid.
-
° Including an explanation of how a decision compares to the model/supporting analysis (even if the decision is not based on the model output).
-
In practice, the membership of a governance committee is often determined based on who the relevant decision makers are. Therefore, although it is possible to encourage different personalities or cultures on a committee, this cannot be guaranteed, and furthermore the members will regularly change as people in the organisation move around. However, it is feasible and recommended to ensure that the MI presented at the governance committee embraces and addresses the challenges of the different types of cultures, in order to give the best chance of securing committee approval and of withstanding any challenges raised upon escalation, that a model is fit for purpose. This does not necessarily mean that all of the four perspectives must be presented at the meeting, but that model owners are equipped with the right information to meet the expectations and challenges of all stakeholders.
3.4.3. Challenges
Implementing the principles of model governance outlined above will be challenging and can only be achieved within a broader corporate culture that accepts difference, encourages dialogue, and does not penalise dissent. Incorporating a variety of possibly conflicting perspectives in governance will always be a challenging and fraught process. Solutions to model governance questions will be arrived at through uneasy compromise and may sometimes lack coherence. This is an unavoidable consequence of the diversity of cultures typically existing within an organisation. To manage this challenge, communication within the organisation must emphasise the validity of all four perspectives on risk and on modelling. In our experience, even people who subscribe strongly to their own distinct professional identities are perfectly capable of understanding the complementary wisdom of others. We hope that our analysis, as summarised in Figures 5 and 7, can provide a helpful tool to foster such mutual understanding.
A related challenge arises from external pressures, particularly those of regulation. Solvency Capital Requirement (SCR) calculations under Solvency II, requiring the quantification of extreme loss percentiles, are subject to a very high degree of model uncertainty. Different models, all consistent with available empirical evidence and expert judgement, can give radically different SCR values.Footnote 8 This makes solvency capital calculation a natural domain for the kind of multi-way dialogue that we envisage.
At the same time it is not clear whether a regulator could plausibly accept the legitimacy of all four perspectives on models that we consider here, in particular the Intuitive Decision Maker view from the top-left quadrant. For instance, would the following statement ever be acceptable in the context of regulatory model review?
“Assumptions are consistent with empirical evidence and best modelling practice. Model uncertainty remains high. The precise model calibration is such that standard outputs are also consistent with senior management’s perspective of a commercially reasonable capital requirement”.
One can easily imagine model reviewers (either internal or external) balking at the idea – or at least its open statement – that the convenience of the model output to management should influence the selection of assumptions. To accept that, one would need to accept the legitimacy of the perspective of Intuitive Decision Makers, who will often show greater concern for the commercial implications than for the accuracy of models.Footnote 9
Accepting such a perspective would be uncomfortable for many market participants, plausibly including regulators. But denying its existence and its legitimacy can deprive an organisation of the tools necessary for controlling and counterbalancing the influence of Intuitive Decision Makers. For example, by pretending that only technical arguments are legitimate in the context of model validation, perverse incentives may be created. On the one hand, if management cannot be seen to let commercial incentives influence model selection, Conscientious Modellers may feel pressurised to provide the “right answers” and thus avoid the tough questions that need to be asked in model validation – thus their professional ethos is undermined. On the other hand, if management’s role in model selection is not acknowledged, it becomes easier to blame business failures on flawed models rather than bad judgement.
In this way, the quest for objectivity inherent in excluding the perspective of Intuitive Decision Makers does not actually result in a higher technical standard of modelling; instead it damages accountability. Good governance, as well as good science, requires transparency. For this we need more – not less – politics, with all the noise and uneasy compromises that engaged dialogue involves.Footnote 10
3.5. Summary
In summary, in the current chapter we argued that:
-
- There are four distinct perceptions of modelling and it uses, each generating its own type of (non-)model risk. We call the holders of those, Confident Model Users, Conscientious Modellers, Uncertainty Avoiders, and Intuitive Decision Makers.
-
- These perceptions are complementary and they all need to be represented and responded to in model governance. This expands the set of legitimate challenges that are typically considered, by including operational and commercial considerations, in addition to purely technical ones.
-
- Although in some applications a particular perception of models may be seen as more appropriate than others, multi-directional challenge is still needed to guard against complacency and to enhance adaptability of the enterprise.
-
- Given the fundamental disagreements between agents about the legitimate uses of models and the likely over-representation of particular perspectives in particular parts of the organisation, specific practical governance measures need to be implemented in order to ensure that all perspectives are represented and responded to.
-
- The inclusion of non-technical, commercially oriented, perspectives in model governance is necessary, even though possibly uncomfortable for technical model reviewers. Excluding such perspectives can create perverse incentives that actually compromise the technical validity of models.
4. Model Risk Measurement
4.1. Financial Impact of Model Risk
In section 2.7.1, we discussed the idea of quantifying the model risk inherent in a model or model development. This is a challenging and relatively new concept, however it is crucial in effectively managing model risk – as an organisation should understand how large a financial loss their models could cause.
4.1.1. Assessing profitability impact
Models can contain several types of errors, ranging from statistical uncertainty to human blunders. Processes exist for understanding the impact of these uncertainties on the model output.
To quantify model risks in the context of a firm’s risk management, we need to assess the financial impact of model errors on a firm’s profitability. A model output may contain a large error, but the losses to the firm may be small, if the model output is ignored, or if management are aware of model limitations and adopt strategies to mitigate model risk. On the other hand, a small model error may have large consequences if important decisions rely on the model output.
We now describe, therefore, some ways to link model error to corporate losses.
4.1.2. What is the baseline?
All models are wrong, and all outputs are subject to some form of error (or at least this would be the view of all but the “Confident Model User” of section 3). Just as with credit risk, lenders expect a certain rate of default losses, so anyone using models should expect these models to contain a certain rate of error.
We might often suppose that expected model errors are zero; that human blunders are as likely to lead to overstatement or understatement, and that unbiased statistical estimates are correct on average. The expected model error may be zero, if, for example, a model is as likely to understate as to overstate the output, and if corporate profits respond linearly and symmetrically to model mis-statement. On the other hand, there are costs associated with model changes, such that the expected financial impact may be related to model output volatility rather than the expected value. In general, we may then want to split model error into two components (as is typically the case with credit risk):
-
- Expected model error, that is, the losses expected under a model containing a baseline degree of model error. For an insurance company, if the cost of historic model errors has not been separately split out from other expenses, then expected model errors should be captured in historic expense analysis and form part of technical provisions (reserves).
-
- Unexpected model error, that is, the contingent financial impact of higher than expected model errors. It may be necessary to allocate capital to this form of error, allowing for an appropriate degree of diversification in the context of a firm’s overall risks.
In the next few sections we consider several possible model applications, in pricing, hedging, product administration, financial reporting, and capital management. In each case, we offer some suggestions for how model error may generate financial losses. Model review and validation are generic ways to mitigate model risks; in some places we mention specific mitigation strategies for particular model applications.
4.1.3. Models used in pricing
Modelling is a vital part of the pricing for financial products sold to the public. There are typically at least two elements to the pricing. Most familiar to actuaries are models of the product cashflows whose purpose is to assess the cost to the firm of providing a particular product, including insurance claims and administrative expenses. The second component models the customer’s propensity to buy as a function of the price charged, that is, the price elasticity of demand.
If we can accurately predict demand at a given price level (i.e. model errors are in the cashflow model and not the propensity model) then the financial impact of model error is modest: it is the extent of the error in cost estimation multiplied by the business volume from the demand model.
The more complex case arises when both the cost and the demand are unknown, but the errors in each are negatively correlated. This can arise in price-competitive markets, where competitors may have access to different information and customers are more likely to select cheaper providers. In this case, firms attract the greatest volumes where they have under-priced the business relative to competitors, which is more likely than not to imply under-pricing in absolute terms. In this case, the expected cost of model error should reflect the negative correlation effect. The Winner’s Curse GIRO Working Party Report by Rothwell et al. (2009) provides possible methodologies for this based on auction theory.
We have described applications to pricing of insurance products. Similar issues occur in asset selection, where managers may compare asset market price with the subjectively assessed value of that asset to the insurer, assessing whether the asset is cheap or dear. As with the pricing of customer products, the real problem here is correlation: investors will hold more of an asset they deem to be undervalued, and their assessment of aggregate value to them is therefore likely to be overoptimistic.
How might firms mitigate these model risks? One possible approach is apparently crude risk-appetite limits, not to invest more than a maximum proportion of a fund in any asset class, not to write more than a maximum premium in any line of business or customer segment. In the context of product pricing, firms can keep an eye on competitor prices, to flag any situations where an increase in uptake may be due to under-pricing.
4.1.4. Models used in hedging
Models used for hedging of market risk typically involve calculation of the so-called “greeks”, which are sensitivities of assets and liabilities to defined moves in risk drivers such as interest rates or equity markets. Hedging means trading in such a way that net greeks are zero and there is no portfolio sensitivity to small moves. Firms may not necessarily seek to hedge all risks; exposure to equity and credit markets may be retained strategically in order to collect an associated risk premium; other positions may be tolerated within limits where the transaction costs of hedging are believed to exceed the benefits.
Models may mis-state the greeks for a number of reasons. There may be coding errors or inaccurate valuation approximations. There may be sampling error for Monte Carlo models or other errors inherent in discrete option pricing models. There may be supplementary assumptions, for example, relating to policyholder persistency or longevity; errors in those assumptions may also cause the greeks to be mis-stated. Not all apparent errors in greeks turn out to be errors; a difficulty reconciling greeks to movements in valuation results could be due to an error in the valuation model. When we consider the financial impact of an error in calculating greeks, the real financial impact relates to an inconsistency in the greeks’ calculation and the valuations from which the greeks are, in theory, derived.
If a firm miscalculates its greeks, it may labour under a false impression of being hedged, leading to an unrecognised exposure to adverse market moves. There may be some debate about how these moves are attributed, in particular, whether they are considered as market risk losses or model risk losses, with neither the traders nor model builders keen to accept responsibility. In theory, a similar dilemma exists for profits, except that it may be politically astute for the traders to take credit for a fortuitous market move, which, nonetheless, reflects badly on their model (hence the model builders). There may then be an asymmetry in how costs are apportioned, with models blamed particularly for losses. This embedded option could imply a substantial cost of model risk, but in aggregate terms this should be seen in the context of the corresponding positive option in the measurement of market risk.
The unexpected model risk cost relates to the scale of possible errors in the greeks (relative to the valuation model), multiplied by the volatility of the underlying risk driver.
Model risk mitigation strategies (i.e. as per section 2.9) may include limiting a firm’s exposure to complex designs for policies, products, or derivatives for which the greeks are difficult or complicated to calculate; in addition to more generic mitigation activities (validation, parallel calculations, spot checks, etc.).
4.1.5. Models used in product administration
Models are widely used in the administration of financial products. These can include routine matters such as the crediting of interest to managed accounts, deduction of mortality charges, or calculation of surrender values. Models are also used for more complex purposes, such as the determination of bonus rates on profit-sharing business. There are frequent press reports of customers being short-changed by financial services providers, and the problems being blamed on computer systems. There may also be false alarms, with suspected problems being due to errors in validation checks rather than in the original coding.
The costs of such model errors can be considered in three categories:
-
- First, there are the direct costs of remediating any error. These might include writing to customers, computer code re-writes, costs of managing regulator relationships as well as any fines for financial conduct breaches. These are likely to be quite significant.
-
- Second, there will be the cost of compensating affected customers. In general terms, some customers may have been over-charged and others under-charged. The cost is the total effect, recognising the asymmetry that clawback from under-charged customers may not be possible, that is, the model risk cost of compensation is likely to be asymmetric.
-
- Third, there may be some reputational risk, whose impact is much more difficult to quantify, in part because a good reputation is not generally recognised as an accounting asset, and so its impairment generates no accounting loss. The reputational risk is similarly asymmetric.
Measuring expected model risk losses may be difficult for both political and technical reasons. Politically, few firms would admit tolerating any non-zero level of regulatory breaches, even though in practice breaches do occur. From a technical perspective, we might argue that the average impact of errors is zero, as coding errors are equally likely to result in under-charging as over-charging.
However, as alluded to above there are several elements of asymmetry which lead to a positive expected model risk cost:
-
- Refunding customers who have been over-charged requires no customer consent, whereas clawing back overpayments involves customer cooperation, many of whom will claim to have spent the money.
-
- Over-charged customers may also claim for consequential losses, such as interest or overdraft charges.
-
- Where customer complaints form part of the process for error monitoring, mistakes in customers’ favour may escape detection for longer.
Unexpected losses would result from unexpectedly large model errors, leading to regulatory breach and compensable customer harm.
4.1.6. Model use in financial reporting
Errors in financial reporting models may result in mis-statement of firms’ profits, assets, liabilities, or capital requirements. The impact of the mis-statement depends on the use to which the financial statements are put.
There is a particular circular reference for model error in financial reporting, because the engine that contains potential errors is also the tool for reporting those errors. Where profits have been historically overstated, recognition of the model error may take the form of a downward restatement of past profit, rather than the recognition of a current loss to offset previous exaggerations. Given that the most vulnerable parts of many accounting systems are the valuations of complex assets and liabilities, any mis-statement will often only shift profit from one year to another and therefore could on the face of it be seen to self-cancel. However, it is also possible for errors in valuation to lead to direct financial losses – for example, if a company undervalues an asset and sells it for less than it is worth. Furthermore, investors place significant emphasis on published financial reporting numbers, and sharp unexplained movements can be costly. (For example, in 2009, one of the largest insurance companies in the United Kingdom lost a third of its stock market value, by changing the model it used to report embedded value figures. The new modelled results were more technically correct, but the model change was not sufficiently well signalled to the investor community.) We want to quantify the model error loss, but the amount of the accounting mis-statement is a difficult place to start.
Instead, examples of possible model risk losses include the following:
-
- Poor management decisions on the basis of reported numbers; for example, the decision to invest in a line of business which appears to be profitable but, after correction of a model error, is found unprofitable.
-
- Executive compensation paid on the basis of overstated profits.
-
- Losses sustained by third parties as a result of flawed decisions to invest in a particular business (or to refrain therefrom), either through purchase of shares or merger/acquisition activity.
-
- Legal and other costs of litigation claims resulting from accounting mis-statements.Footnote 11
It is in the nature of public financial reporting that (alleged) losses may be sustained by a large number of potential investors, over whom the firm has little control. They may seek to recover losses via legal action, despite the obvious fact that, in taking legal action against corporate management, the investor risks damaging the very investment whose poor performance was the subject of the original complaint. As for many elements of model risk quantification, the asymmetry is key. A buyer’s investment loss is a seller’s lucky escape, but only those sustaining the loss seek compensation.
In the financial industry, losses sustained by investors have not generally resulted in litigation claims against management. And, furthermore, so far the question of “how valid is the investor’s model” has not been a central feature of any such legal action (as it is in legally contested disputes over environmental protection; section 4.5). Rather, the claimant must demonstrate that their investment decision relied on the erroneous disclosure; a possible defence is that the investor would have invested anyway. In particular, this largely eliminates actions based on favourable accounting restatements.
To mitigate this form of model error losses, firms could, for example, survey the users of their financial statements to understand the uses to which they are being put, which accounting elements are most used and whose mis-statement could give rise to the largest alleged losses.
4.1.7. Model use in capital management
Models are widely used in capital management, for example, in determining the quantity and quality of capital a company is required to hold against its various risks. Capital models often deal in extreme percentiles and so are particularly vulnerable to statistical error. This is where the views from the Uncertainty Avoiders and Conscientious Modellers in section 3 should be welcomed. In addition, as this is a relatively more complex area of modelling endeavour, the models may be more prone to containing undetected coding errors.
As with published financial statements, the chief sources of model error in capital management may involve the consequences of poor decisions relying on those models. For example, a mis-estimation of required capital may result in a mis-statement of the cost of capital. However, there is some debate over whether the cost of required capital represents a true economic cost; and how the partition of capital into “required” and “surplus” affects that cost. It might seem, then, that errors in stated capital requirements would give rise to only a modest economic cost.
Instead, to measure the model risk cost, we need to consider more extreme scenarios, in particular when there is a debate over whether a firm should be allowed to continue trading. For example:
-
∙ Where a firm is wrongly prevented from writing profitable business, there may be a loss of franchise value to shareholders in view of the future profits foregone. If the insurer’s shares are traded then the loss in franchise value may be directly observable. Even where they are not, there may be a corresponding benefit to competitors, and a possible overall consumer loss due to reduced competition.
-
∙ Where a firm is wrongly permitted to write business, there may be losses to the extent that business is unprofitable. Consumers may face default if the firm is unable to meet all of its liabilities. On the other hand, firms continuing to write business, even if under false authorisation, may preserve their franchise value which is a benefit to shareholders.
From a shareholder perspective, the possible model error losses therefore mainly relate to the risk of wrongly triggering regulatory intervention. As with other model risks affecting reputation, converting model risk into a shareholder loss is complicated by the inadmissibility of the reputation or franchise value as accounting assets, so their loss is not recognised as a cost in the accounts.
Most firms have robust validation, controls, and governance in place against the risk of capital mis-statement for regulatory and commercial reasons.
4.1.8. Model use in customer financial planning
Our last model application considers the use of models within the sale process, for example, to consider an appropriate mix of different assets.
We can consider the model risk from the perspective of the saver and the savings provider.
Measuring the model risk ex ante is difficult. If the “correct” model and the investor’s utility function were known, then we could compare the expected utility of the recommended strategy with that of a theoretically optimal strategy. Not knowing the correct model makes this calculation more difficult.
The Monte Carlo back-test gives us a possible solution. This involves distinguishing a “reference model” that governs both past and future outcomes, and a “fitted model” that is an imperfect attempt to model the future based on only the historic data. By simulating multiple past-and-future scenarios from a reference model and then computing a fitted model, we can investigate the consequences, from the investor’s perspective, of using the fitted model (rather than the unknown reference model). There is a catch though – the conclusions depend critically on the choice of reference model.
From the saving provider’s perspective, the chief model is of compensating investors for losses deemed to be due to poor advice. The quantum of damages is usually based on the cost of restoring investors to the position they would have been in, had “correct” advice been given.
To give rise to a claim, a plaintiff has to demonstrate a quantum of loss. Successful compensation claims have historically not been on the basis of expected utility but, instead, a more tangible hindsight comparison to alternative strategies. This means that, for example, a client who loses money on a risky investment, may allege poor advice and claim compensation to restore them to the position they would have been in had they followed a more conservative investment strategy. It is legally much less common for investors in low-risk products to gain compensation on the grounds of returns foregone on well-performing risky products they wish they had bought.
The calculation of compensation therefore has a substantial embedded option. In a bull market where risky assets perform strongly, investor compensation is unlikely to be required, irrespective of the basis of the advice to acquire those assets.
Market downturns create unhappy investors, some of whom will seek compensation. The compensation awarded requires more than an investment loss; the client must demonstrate a link to poor advice. In most cases, this link is not directly model related; for example, an agent may have failed to ask the right questions in a fact find, or may have deliberately recommended unsuitable products, for example, in order to maximise commission.
Where a model error is the primary alleged cause of bad advice, the most likely grounds for complaint is that a model claiming to show a probability distribution of outcomes failed to highlight risks that actually materialised. For example, a model of corporate bond returns based on data from the 1960s through to 2007 may have assigned a very low probability to the outcomes seen in 2008/2009.
As it happens, stochastic models were not widely used in financial advice before 2008, so we have little experience by which to judge possible compensation. However, one possible argument would be to treat losses beyond the largest illustrated loss as a consequence of bad advice. Thus, even when firms explain that every penny is at risk, there is a risk of having been deemed, with hindsight, to have written a put option struck at the worst individual scenario actually shown to the client.
The easiest way to mitigate the risk of compensating bad advice is to avoid giving advice in the first place, for example, by offering an execution only service. Where advice is given, a risk mitigation strategy could be to advise all customers to hold low-risk assets. Where risky strategies are sometimes recommended, a balance in financial advice is needed. The more adverse the worst illustrated case, the lower the likely quantum of any compensation, but less the chance of attracting the investment in the first place.
4.1.9. Conclusions on quantifying the financial impacts of model risk
There has been much recent research on model risk, seeking to quantify various components of uncertainty in model output. Here we have focussed instead on the consequent losses sustained. We separate the model risk loss into expected and unexpected components.
In many cases, the model risk appears at first sight to be symmetric, with equal likelihood of an overstatement or understatement. Further consideration, however, reveals various forms of embedded optionality whereby firms can gain little advantage from a favourable model error while retaining substantial downside exposure. The relevant model error typically turns out to be the difference between two models, rather than a hypothetical difference between a model and the truth of the matter. Quantification of the model error impact involves a valuation of that option.
4.2. Application To Proxy Models
4.2.1. What are proxy models?
Firms seeking to model a full distribution of losses, or changes in basic own funds, over the next year for capital calculations often find that their asset and liability cashflow models take too long to run to practically allow such a distribution to be constructed by repeated simulation. Therefore, they calibrate approximations to the cashflow models, called proxy models, which benefit from much improved speed but introduce approximation errors. Proxy models are special in the sense that the model error versus the underlying model is more precisely quantifiable than for other model types.
Model risk for proxy models is the risk that decisions are made based on proxy models which are different from those that would have been made on the cashflow models (if the latter could have been run frequently enough to build the loss distribution).Footnote 12 Such a risk arises because there is model error, or approximation error, between the cashflow model and the proxy model and this error is not understood by the decision makers and other users of the model. Below we discuss techniques for assessing model error and see how this gives us a way to identify, measure, monitor, manage, and report the resulting model risk.
4.2.2. Definition of model error
We can define model error as the difference between the cashflow model and the proxy model outputs at particular percentiles where the model is used. For example, if the model is used to calculate Solvency II SCR, then a percentile of interest would be the 99.5% change in basic own funds over the next year.Footnote 13 However, practically we do not have the ability to build a full loss distribution from the cashflow models and compare the 99.5th percentile with that obtained from the proxy model, so we cannot measure for certain the loss at any particular percentile. What we can usefully do is sample scenarios from the proxy model output and calculate the corresponding losses from the cashflow models, in such a way that we can build a picture of likely errors around these key percentiles. We call these out-of-sample (OOS) tests to indicate that they are separate from the in-sample scenarios used to train the proxy model. Having defined model error in this way, we proceed to discuss how this helps us control this risk.
4.2.3. Risk appetite
Model risk management should involve a stated risk appetite. The risk appetite should be linked to the decisions that will be made using the proxy model, and the required accuracy for those decisions. For example, the proxy model will be used to calculate the Solvency II SCR at group and local levels. A particular business unit CRO might require this SCR to be accurate within 5% to be used in decision making. This SCR is “local” in the sense that it applies to that particular business unit, and distinct from the SCR calculated at a group level.
This leads us to two useful conclusions. First, model error could be measured, monitored, and reported as a proportion of local SCR. This sounds easy in theory, but there are complications in practice which will need to be considered. For example, a proxy model for a With-Profit Fund might calculate a notional SCR before management actions, SCR(1), and the management actions are out-of-model adjustments which reduce this to another value, SCR(2). Model errors expressed as a proportion of SCR(1) will be smaller than when expressed as a proportion of SCR(2). The problem becomes even worse if the proxy model becomes more granular and calculates components of the notional SCR, like the shareholder burn-through, where most of the time the cost is small but in extreme events increases dramatically.Footnote 14 Where the 99.5% VaR of the burn-through is small, model errors will appear large as a proportion where these extreme events are included. Therefore, it is important to have a comprehensive definition of what the risk appetite means and how it is calculated.
Second, as per section 2.4, model error risk appetite should be set by the Board and Senior Management users of the model. A bottom-up approach, where local CROs and AFHs decide on their appetite for taking on model risk and measure model performance against this is preferable to a top-down one where model error is measured at the Group level and allocated back down to local businesses. The danger of the second approach is that risk-appetite setting will be driven by what the model can do in practice, rather than what is required for decision making. For examples of three problems with a top-down approach, assume that at a group level the proxy model is within 10% of the heavy model, based on a sensible model error definition, and this is taken to be the risk tolerance. Allocating 10% tolerance back down to local businesses (a) might not be appropriate where a 5% model error at most is needed for decision making because of a small capital buffer for that local business unit, say, (b) ignores the fact that some errors net off, and are overstatements for some businesses and understatements for others, and (c) does not allow for local SCRs being composed of different risks than the group SCR.
4.2.4. Model fitting methodology
Proxy model calibration in practice requires finding coefficients, or parameters, for some choice of smooth function of the risk drivers. These “basis” functions are the structure of the model, and tend to have one of three forms: polynomials, orthogonal polynomials, or splines. There are also three common methods that could be used to fit, or find the coefficients for these functions: least squares, minimising the maximum error or Least-Squares Monte Carlo (LSMC).
A polynomial of order 6 for a single risk driver, x, is as following:
There are seven parameters to estimate, and this is the number of basis functions, q, which determine the maximum possible flexibility allowed for a smooth term. For example, q equal to 10 will yield a “wigglier” non-linear estimate as compared with the estimate that is obtained when this parameter is set to 7. The drawback of simple polynomial basis functions is that, as the number q increases, the polynomial becomes increasingly collinear. This yields highly correlated parameter estimators which may lead to high estimator variance, numerical problems, and instability. The problem is one of picking the optimal value of q. Sometimes, statistical theory is used to try and select such an optimal value. However, note that the statistical theory makes assumptions about the distributions of the errors in such models (independent and identically distributed) which do not hold in practice.
The problems of correlated estimated parameters can be overcome using orthogonal polynomial bases. For example, consider a call option on an underlying instrument that might return any value between −1 and +1 over the next year. If we were to fit the option pay-off function (black line in the left panel of Figure 8) by sampling at eight equally spaced points (black circles), we would get the fit in the red line whether we used simple polynomials or orthogonal polynomials.

Figure 8 Fitting an option pay-off with an order 6 polynomial (left panel) and order 20 polynomial (right panel)
However, the correlation matrix of the estimated parameters in the orthogonal polynomial case would be 0% (except for the leading diagonal, also known as the identity matrix), whereas in the simple polynomial case it would be as follows (Figure 9).

Figure 9 Highly correlated parameter estimators in the simple polynomial basis which may lead to high estimator variance
Another word of warning: using equally spaced points is likely to lead to disastrous consequences at the extremes for higher-order polynomials.Footnote 15 In the example above (right panel of Figure 8), we also fitted the option pay-off as before (black line) with an order 20 polynomial – note the errors at the extremes and the change of scale.
However, from a theoretical point of view, polynomial bases (simple or orthogonal) are more useful where interest focusses on the properties of f(x) in the vicinity of a single specified point. When interest relates to fitting the whole domain of f(x) then spline bases are used. Spline bases are not as correlated as polynomial bases, allow for more flexible non-linear relationships, have convenient mathematical properties to allow inference and good numerical stability. We have seen some firms use cubic splines as basis functions. A cubic spline is a curve, made up of sections of cubic polynomials, joined together so that they are continuous in the values as well as first and second derivative. The points at which sections join are known as the knots of the function. For conventional splines, the knots occur wherever there is a datum, but for regression splines the location of the knots must be chosen. For regression splines, the knots would either be evenly spaced through the range of observed x values, placed at known turning points of the function or placed at key quantiles of the distribution of x values. Fitting will involve penalising functions which are too “wiggly”, and trading off over-smoothing the data with under-smoothing it (known as cross validation).Footnote 16
Any of the model structures (with basis functions consisting of simple polynomials, orthogonal polynomials, or splines) above can be estimated by least squares, a common technique which minimises the error defined as the sum of squares of the individual errors. Least squares fitting is strongly influenced by the distribution of x values chosen, and equally spaced x values will lead to large errors at the extremes. Note that it is not the case that the proxy model will always overstate extreme percentiles. In Figure 10 (left panel) and Figure 11 we fitted an option pay-off (black line) with an order 6 polynomial and we can see that the extremes of this function are understated by the proxy model. Figure 11 (right panel) also shows the errors for each quantile, Q, calculated as the values given by the proxy model at Q minus the values of the actual model at Q (where the actual model is termed “heavy model” to make the example pertinent). Note that in fitting the proxy model, we make no assumptions about the distribution of the underlying. In Figure 11, we made the assumption that the underlying has a normal distribution with a 99.9th percentile stress of +1 and a mean of 0. Errors are shown between the 0.5th percentile and the 99.5th percentile (the dotted blue line) to keep the resolution manageable. Note from Figure 11 (left panel) that errors at the points beyond the calibration interval [−1,+1] explode due to the turning points near the extremes, particularly noticeable below a value of −1.

Figure 10 Fitting the examples above with a cubic spline basis: visually, 20 knots seems to overfit the data

Figure 11 Fitting an option pay-off using least squares (left) and errors from a Normally distributed underlying (right). Note that errors explode outside of the fitting bounds and so the errors graph is bounded between the 0.5th percentile and the 99.5th, to keep the scale manageable, otherwise the large error at the extremely small percentiles would dominate
An alternative would be to fit to a different objective, and aim to minimise the maximum error. Algorithms are available that fit an orthogonal polynomial for functions of one variable. For multivariate functions, this tends to be much more difficult.Footnote 17
Fitting by minimax would be theoretically the best option if by “best” we mean that we want to know and control the maximum error.Footnote 18 However, the method suffers from the drawback that many iterations might be needed to choose the fitting points (x values) at the right places so that the maximum error is controlled, and this might be expensive in terms of runs of the heavy cashflow model. However, once a minimax fit is achieved, we would know what the maximum model error was at any percentile, regardless of distributional assumptions as long as we stay within the fitting interval (Figure 12).Footnote 19

Figure 12 Fitting an option pay-off using minimax; note that the errors from a Normally distributed underlying are bounded between known intervals (within the fitting bounds)
Fitting the same eight equally spaced data points on our pay-off function with regression cubic splines with five joining points or knots, we get the graph in Figure 13. We used no penalty function for smoothness (as there are few data points and we know that our function is not smooth). Note that the largest error occurs at the underlying value of 0, because our equally spaced data point selection did not result in a datum at the kink in the function. However, the errors at the extremes are clearly very small, and the errors overall could be further improved with better selection of the function values sampled and knots.

Figure 13 Fitting an option pay-off using regression cubic splines; note that the errors from a Normally distributed underlying are small at the extremes
Lastly, another fitting technique used in practice is LSMC. This requires many “noisy” heavy model runs (or inaccurate cashflow model calculations, based on fewer “inner” scenarios to keep running times acceptable) for many risk stresses (“outer scenarios”), and fits a polynomial by least squares to the results. The accuracy of the resulting proxy models from this technique are difficult to summarise, as the algorithms and implementation are largely proprietary to a few consultancies and software vendors, and results will depend on the algorithm for choosing the optimal polynomial basis order q.Footnote 20 Generally, LSMC needs just as much rigorous OOS testing, if not more so because (a) there is potentially less transparency when working with proprietary algorithms and (b) there is no other way (than OOS testing) of establishing how the lower accuracy of the noisy cashflow model results affects overall accuracy.
Regardless of which model structure and fitting method is used, our view is that these are either standard techniques from other fields with a new application to insurance portfolios, or entirely new techniques. Much caution is needed, and the proof of any particular proxy model fit should be demonstrated with OOS error testing and good validation to demonstrate that the proxy model does what it sets out to do, which is to approximate the heavy cashflow model.
4.2.5. Model validation
Model validation should be linked to model use. We might be keen to ensure that our model is accurate around the SCR (and other quantiles of the loss distribution where these are used), but as the discussion in the previous section highlights, model errors mean that we cannot confidently say that the 99.5th quantile of the proxy model corresponds to the 99.5th quantile of what the heavy cashflow model would predict. Sometimes we are understating and sometimes overstating, and this leads to a reordering of the scenarios. Therefore, testing a range of quantiles seems sensible. Furthermore, the sort of scenarios that represent a Group SCR might be very different from those that make up a local SCR, or a notional SCR for a particular fund. Therefore, extensive testing is needed at the Group, local and fund level (and possibly below that, e.g., in the case of the with-profit burn-through model discussed at the start of this section).
Sometimes to avoid bottlenecks around the reporting date, firms calibrate proxy models to previous exposure data, say one quarter out of date, and roll the results forward. This can only introduce more model error.
Therefore, good practice might be that model validation should:
-
- cover roll-forward between calibration date and use date;
-
- cover appropriateness for different lines of business;
-
- cover appropriateness at local level and for group solvency calculation;
-
- include “combined scenarios” under which more than one risk factor is simultaneously stressed within their universe of OOS tests, such as key percentiles of the overall loss distribution; and
-
- cover a range of the loss distribution, not just the SCR quantile, and link this to model use.
Having established that we carry out validation of the model error around the key percentiles of model use, good practice would be that this is linked to the risk appetite set at the beginning of this section. The risk appetite should define what acceptable validation results represent. It should be possible to explain why the acceptance criteria used are appropriate and show how this links back to the confidence interval around the SCR (at a fund, solo, or Group level).
If the risk appetite is for OOS errors demonstrating that the proxy model does not mis-state the SCR by >5%, then the validation activity should detail the process to be carried out if validation exceeds this. For example, maximum OOS errors of 3% or less would mean that there is low concern, 3–5% could lead to further investigation of the outliers and possibly more testing to be able to justify why these do not cause a material mis-statement of the SCR, and 5% or more should lead to more severe actions. More severe actions could range from accepting that the proxy model is not fit to be used for this reporting cycle, or holding capital for model error in the short term so that the SCR is not understated. Solvency II requirements seem to require such actions: for example, the Solvency II Delegated Acts Article 229(g) states that
“Actuarial and statistical techniques shall only be considered adequate, applicable and relevant […] where all of the following conditions are met: […] the outputs of the internal model do not include a material model error or estimation error; wherever possible, the probability distribution forecast shall be adjusted to account for model and estimation errors”.
In all of the validation activity above, it is important to test that each risk is not stressed beyond the bounds used in fitting the proxy model. We would therefore suggest that another good check is to verify that, for each OOS scenario investigated, the component risks are not stressed beyond the fitting or operational bounds. We can then make statements like “this proxy model is accurate to within £1m or 1% of SCR, provided interest rates remain within [0%, 20%], lapses remain in [0%, 50%], equity moves in [−80%, 250%]”.
Model validation and model governance should drive a cycle of model improvement: model validation results should drive the effort for the next cycle of model improvement, and point to areas which need further research.
4.2.6. Model governance
We have so far discussed that proxy models are a special case where, in principle, we can put definitive limits on the model error. The next part of controlling model risk involves communicating those results effectively to decision makers, and for those decision makers to use this information in their decisions.
Model developers, on the one hand, should be wary of giving false comfort on the accuracy of the proxy model even when the materiality of approximation error is so high. We make the link to the four different perceptions of modelling that are discussed in section 3 and depicted in Figure 5. The bottom right quadrant (Conscientious Modeller) works out the limits of model fitness for purpose and tries to communicate those. This is in contrast to the top right quadrant (Confident Model User) who prioritises an operational perspective and does not focus sufficiently on model errors. In a sense, therefore, the Confident Model Users’ model would be so complete – including even the kitchen sink, as it were, in having arrived unambiguously and incontrovertibly at the truth of the matter – as to be self-evidently fit for any and all purposes. We would suggest, therefore, that a statement of the model error should be included whenever possible when reporting results from the proxy model. A good maxim for model developers can be found in Derman and Wilmott’s “The financial modeller’s manifesto”: “I will not give the people who use my models false comfort about their accuracy” (Reference Derman and Wilmott2009). Furthermore, it should be noted that a dialogue between primarily Confident Model Users and Conscientious Modellers pertains to the nature of model risk arising from proxy models: a purely technical problem of approximation error. However, at some stage, the issue of uncertainty around the full model (subsuming considerations of approximation error) will have to be considered. At that point, agents who are sceptical about model use (the left half-plane in Figure 5) would struggle to see the utility of wasting time and resources “trying to model a model”. Uncertainty Avoiders hold that no model is valid or fit for purpose and, in (for them) an enduring crisis, there is just no time for the luxury of modelling. Intuitive Decision Makers, on the other hand, if obliged to use a model or be judged for having used a model, can make use of it by stretching its results every which way to suit their needs – a discussion of the model’s potential errors is beside the point for them.
The model owners, on the other hand, have a duty to make the limitations of the proxy model transparent, and for the model only to be used if the limitations are properly understood and taken into account in decision making, in line with the Model Risk Management Framework. In particular, they should ensure that there are tolerance limits around model error, and that such limits are linked to decision making.
Setting a tolerance limit around model error should be linked to how the results are used. Given the prominence of a proxy model in a firm’s capital planning, and that proxy modelling invariably introduces approximations, it seems to us that model error should be communicated to all stakeholders including the Board. The Board must understand the limits on the accuracy of the model. The Board’s risk appetite, its understanding of the inaccuracy of the SCR outcome and the ORSA level of buffer capital are all important aspects of controlling model risk in proxy models.
If Boards use results with the understanding that they are within ±5% and set risk appetite and capital management policies in this context, then an error limit up to 5% seems sensible, but anything higher should be escalated. If this tolerance limit is exceeded, a set of escalation actions should be predefined. We have discussed that they could involve reporting to the right committees and holding additional capital in the short term for model error. In the longer term, an exercise to investigate the fit of the proxy model might be appropriate.
4.3. Application To Longevity Models
4.3.1. Importance of longevity risk
Longevity in the context of the insurance industry, how long pensioners and annuitants live, is especially important for markets such as the United Kingdom where many people buy annuities to provide post-retirement income. Although it is unclear exactly how the post-retirement market will change in the United Kingdom since the budget announced in March 2014 – which removed the requirement for retirees to purchase any form of annuity – it is still likely that longevity will remain one of the most material individual risks faced by insurers, in part due to the long duration of longevity product liabilities and the expectation of new innovative retirement products being marketed in response to the budget announcement.
Put simply, an insurer who overestimates longevity may be unable to generate business in a price-competitive market. An insurer who underestimates longevity may win a lot of business, which subsequently turns out to be unprofitable, sometimes labelled “the winner’s curse”. There are costs associated with errors in either direction (just as discussed in section 4.1).
We can derive longevity assumptions from different populations, which introduces risk. First, there is the estimate of longevity for the national population as a whole, and second, there are basis effects associated with the sub-population of a particular insurers’ policyholders. The basis effects might occur because the insurer has a non-representative mix, for example, of levels of wealth, gender, smoker status, or other attributes known to affect individual longevity. Insurers marketing products with new business flow (i.e. future vestings) are more exposed than those engaging in transactions of large inforce blocks of annuitants, such as pension scheme buy-outs, as the anticipated policyholder mix when pricing could be materially different for the former.
In this section, we focus on whole population longevity. Historical data are typically analysed in terms of annual rates of improvement for different ages in different periods. For example, we might compare the rate of mortality for 70-year-olds last year to the rate of mortality for 70-year-olds in previous years. For future projections, the rate of mortality improvement is usually assumed to revert smoothly from recently experienced improvement rates to an assumed ultimate improvement rate. The key assumptions are then the ultimate improvement rate and the speed and shape of reversion from recent improvement to the ultimate assumption. Both of these two assumptions could in principle vary by age, although in practice they seldom do.
In what follows, we consider the drivers of model risk specifically in the forecast of future mortality improvement rates. The model risk here arises when the chosen model is discovered to be invalid, or where an event arises outside of the historical data set being used to calibrate the model that changes the view of future mortality expectations and thereby invalidates the model.
4.3.2. Fisher information approach
We can view the analysis of historical mortality as fitting a two-dimensional surface for the rate of mortality, depending on age of death and on one of either year or birth, or year of death. If we estimate this surface by a form of regression (just as in the discussion of proxy models in section 4.2), there is an implied Fisher information matrix that allows us to construct joint confidence intervals for the various parameters.
Given prediction ranges for the parameters, we can from these construct prediction intervals for future numbers of deaths (given the projected exposed-to-risk). An example of such an approach is the P-spline approach of Currie et al.Footnote 21 This approach seeks to calibrate the uncertainty of future mortality by reference to the volatility of past mortality fluctuations.
Rather than calibrating changes in experienced mortality rates, an alternative approach is to consider the impact of historic revisions in published mortality tables.
4.3.3. Multiple model approach
One difficulty with the Fisher information matrix approach is the assumption that the fitted suite of models contains the “true” model which generated the data. The method is particularly sensitive to implicit or explicit assumptions of independence between lives, which can result in the data deemed to contain more information than is actually the case, resulting in unduly narrow confidence intervals for model parameters. Furthermore, the data itself is just one realisation of what actually happened in practice.
There are several layers of risk, including stochastic risk and parameter risk within a model, as well as the risk of the model being wrong. The calculation of capital using any single model can explicitly allow for these additional elements of risk, but it is the comparison of best estimate results that can inform model users as to the potential impact of choosing one model over another, and can therefore be used as a guide to the extent of model risk (over and above stochastic risk and parameter risk).
Complexity exists when defining the model; for example, are the expert judgements that are applied to the core elements of the model in practice part of the “model”, and therefore within the scope of the model risk investigation? However, when asking the question “how different could the result be if I used a different model?” it is important not to introduce restrictions on either the data or the model fitting methodology, as this can obscure the true variability of the model risk under investigation. Examples include expert judgements such as the use of tapering and linear trends commonly introduced for annual rates of mortality improvements at older ages, along with any restrictions on time series parameters, such as the choice of (p,d,q) for autoregressive integrated moving average models, even though restrictions may be applied to the advocated model in practice for good reasons. In general, applying consistent expert judgements across a range of models is likely to result in convergence of models and hence excluding them from the model risk investigation is prudent.
In addition, we need to consider how the candidate models were originally selected. For example, was a larger set of models originally considered and then some rejected because the forecast longevity was low? Ideally, we want to paint a picture of a larger universe of models (the ambiguity set), filter out the models which are inconsistent with the data, and consider the range of possible forecasts from those that remain.
It could be the case that plausible models produce answers within a relatively narrow range, however, when plausible alternative models produce markedly different answers, the question arises of how to combine those models, or best make use of the information. We could take the average, or the most prudent, or weight the outcomes in some way. If not placing any bias on the particular model being advocated at the time, the comparison of results between n models will produce n(n−1)/2 data points for the potential impact of using different models. The maximum, minimum, and average can be compared with the current methodology of allowing for model risk to determine how prudent this allowance may be. One caveat to this is that the range of plausible models represents those available at the time, rather than the universe of models that may be available in the future.
The range of impacts on capital is evident when competing model families are compared, for example, in the 2013 BAJ paper “A value-at-risk framework for longevity trend risk” by Richards et al. (Reference Richards, Currie and Ritchie2013); the results of which are shown in the table below for a male aged 70 years based on a 1-year VaR approach to capital. The increase in capital between the largest and smallest values is +46%, whereas the increase between the two closest values is just 2%, with the average increase equal to 23%.

4.3.4. Stress and scenario tests
We may decide to change our model if we deem our model is no longer accurate, or a preferred model is developed that better represents our expectations of the future. Or we may decide to change our model if an event arises that was not anticipated and which invalidates our previous expectations. The latter situation is likely to be data driven.
Both the Fisher information approach, and the multiple model constructions, rely heavily on past data and the implicit assumptions that past patterns are in some way repeated in the future. However, we also know that the past data contains some one-off events which cannot be repeated in the same way. For example, the proportion of smokers in the United Kingdom has reduced from around 50% in the 1970s to around 20% at the time of writing. This trend cannot continue, as the proportion of smokers cannot possibly fall by another 30% because there are too few remaining smokers to quit (source: ASH). In addition, it is also hard to investigate the impact on insurers’ historic pricing bases in the market when the health effects of smoking first became publicised in the 1950s as the data is difficult to obtain and collate. So instead we need to ask ourselves “what could happen in the future that could have an impact as big (or even bigger) on the health of the UK population as that witnessed historically?”. For this we need to look ahead and brainstorm scenarios that are a potential threat (and therefore already on the radar in some way) as well as those that have not been widely discussed to date.
The longevity catalysts working party (www.longevitycatalysts.com) asks “what future events are we aware of today whose occurrence is likely to be coupled with a significant impact on UK longevity?”. One approach to this question is to work backwards from cause of death data, and consider the possible emergence of medical interventions that may reduce the prevalence of the disease or treatment effectiveness. The working party has considered the following eight catalysts in some detail:
-
∙ introduction of plain cigarette packaging in the United Kingdom;
-
∙ use of novel diagnostic biomarkers;
-
∙ KRAS-targeted cancer treatment;
-
∙ genetic screening;
-
∙ NHS Bowel Cancer Screening Programme;
-
∙ stem cell therapy and Parkinson’s disease;
-
∙ polypill scenario; and
-
∙ development of a universal influenza vaccine.
Rather than focussing on particular diseases, we could start from the other end and consider forward-looking social trends. For example, we might consider the following scenarios:
-
- There is growing evidence that consuming processed food has a detrimental impact on mortality, mainly through the impact of obesity, but also via cancers arising directly from dietary imbalances, including excessive red meat and lack of fibre. What would happen if future governments confront the processed food industry in the same way previous governments have restricted tobacco?
-
- There is also growing evidence of the mortality posed by environmental pollution, particularly vehicle emissions, on cancers and respiratory diseases. What would be the impact of a future government who pursued more sustainable transport? This could reduce mortality due to vehicle collisions, due to pollution and due to lack of exercise.
It frequently transpires that such stress scenarios fall outside the range of plausible models fitted to historical data. This suggests that the input of forward-looking expert judgement is needed in order to include a reasonable range of future outcomes, and hence when assessing the impact of scenarios such as these it is likely that some approximations will be needed. (Equivalently, sensitivity analysis may illuminate the critical factors in the longevity models whose uncertainty should be reduced as a priority to identify whether the forward-looking scenarios are attainable or plausible.) This does not invalidate the purpose of this exercise, as we are attempting to assess the potential boundaries on the impact of model risk, and stressing our models using hypothetical events can produce valuable information as well as demonstrate that our models are robust when additional data points are included, that is, they react to new data in a sensible way.
4.4. Application to Investment Illustration Models
4.4.1. Background
Financial planning decisions can have a huge impact on people’s lives. At some point in our lives we all have to decide whether to rent or buy somewhere to live, how much to borrow, how much to save, how to invest, and (for those who live long enough) how to convert any savings into post-retirement income.
Traditionally, financial advisors have assisted these decisions using deterministic forecasts. Inherent in these forecasts are many assumptions including those regarding rates of return on different investments, costs of borrowing, future inflation, wage growth, and mortality. It has long been recognised that the asset classes offering the better prospective returns (such as equities) also carry the greater risk of price falls. Investors may also be shown adverse scenarios which are used to illustrate the impact of poor investment returns.
Stochastic economic scenario generators are now starting to penetrate the financial planning process. As a result, investors may encounter claims such as “Your target retirement income is £10,000 per annum. If you invest £xxx per month over 40 years, and invest the proceeds in the stock market, then you have a 90% chance of reaching your target”. In this section, we consider the model risk issues associated with such financial forecasts.
4.4.2. Types of model used
Given the task of using a stochastic model to assess the probabilities of hitting a defined target, the most common starting point is models based on geometric random walks with independent lognormal returns. We now consider these models, and some logical extensions.
Under the geometric random walk model, each asset class is defined by the mean and standard deviation of log returns (measured over annual periods) and different asset classes are then linked via assumed correlations.
The first extension to this model that many actuaries consider is to introduce mean reverting interest rates, so that the rates of interest earned in nearby periods are positively correlated rather than being independent. Expected returns on other assets are usually assumed to fluctuate over time in parallel with interest rates, meaning they are now defined in terms of risk premiums above short-term interest rates.
A single-factor deflator construction may then be applied to construct theoretical behaviour of bond prices, including the pull-to-parity effect (where a bond price approaches the face value as time progresses towards the bond maturity date). The relative volatilities of bond prices of different terms and relative risk premiums are determined by the speed of mean reversion. Thus, there remains only a single risk premium and volatility assumption for a bond of one chosen term, whereas behaviour at other terms is a mathematical construct. The long-run average interest rate may be expressed either in terms of a mean short rate, or an ultimate forward rate for long-dated bonds. These two quantities are related, and so only one can be selected while the other then follows (given the mean reversion speed, bond risk premium, and bond volatility assumptions).
A relatively straightforward further extension is to use distributions with fatter tails such as the logistic or Laplace distributions, in place of normal distributions. If the error terms are taken from an elliptically contoured distribution then the number of parameters is unchanged from the normal case.
4.4.3. Further extensions
It is possible to introduce greater realism (and subsequently greater complexity) by further enhancing the family of reference models. Additional elements might include the following:
-
∙ explicit modelling of price and/or wage inflation;
-
∙ multiple yield curve models (e.g. real and nominal interest rates), or multiple factors for a single yield curve;
-
∙ modelling of volatility and correlations as stochastic processes in their own right; and
-
∙ allowing asset risk premiums to depend on previous returns, levels of interest rates, or on stochastic volatility.
Less commonly the model may also consider mortality stochastically, either pre-retirement or in the form of market annuity rates that reflect post-retirement mortality expectations.
4.4.4. Example model risk calculations
Models for financial planning can already be very complex. Thus, the challenge is to consider models which are relatively simple, but which still capture some essential characteristics of the model uncertainties involved.
As an example we can work in discrete time, with a model that includes bonds and an equity total return index. Bonds have been treated as nominal, but the mathematics could equally apply to inflation linked.
The available assets are as follows: cash (essentially short-term bonds) and 10-year bonds and equities. We assume in our base case that the model has been calibrated to 60 years of historic data. Given the model parameters, and various investment strategies, we compute (by Monte Carlo simulation) the required monthly contribution over 40 years to give a 90% probability of being able to purchase a 20-year annuity on retirement equal (or higher than) to the target income level. The required monthly contribution is then a function of the model parameters. Utilising multiple model runs, we seek to approximate this function with a fitted curve, which we call the “proxy contribution function”.
We can then perform a Monte Carlo back-test where, for a given “reference model”, we generate a 100-year data sample. We use the first 60 years of the data to re-estimate the model parameters to give a “fitted model”. We estimate the required contribution level using the proxy contribution function. Finally, we use the last 40 years of the 100-year sample to assess whether, based on the simulated returns, the investor has met their desired level of retirement income.
Repeating this experiment many times, we can find the probability that the investor meets their target (allowing for parameter estimation error). Although we might hope that the target is met 90% of the time, this is not guaranteed because the 90% confidences were assessed using a series of fitted models and not the reference model that generated the previous 40 years of data.
4.4.5. Stress and scenario tests
One of the strengths of stochastic modelling is its ability to consider a wide range of outcomes and their associated probabilities. For many practical purposes, this is more informative than a best estimate forecast accompanied by stress tests. However, experience has shown that stochastic models often capture some, but not all, of the relevant risks. Thus, it is important that both the risks that have, and those that have not, been taken into account in a stochastic model are conveyed to the model users in a comprehensible manner.
Some elements of missing risks could include the following:
-
∙ Parameter estimates that are inaccurate, for example, because of sampling errors when estimated from limited data sets.
-
∙ Failure to capture structural connections in the economy (or exploiting structural connections which do not exist in reality).
-
∙ Simplifying assumptions about capital markets such as ignoring transaction costs, asset management fees, taxes or default risk with government, or corporate bonds.
-
∙ Assuming that the behaviour of indices is stable over time, or ignoring the basis risk between a fund and the returns on a published index.
-
∙ Failure to capture past or future one-off changes in the world economy, such as the Bretton Woods currency agreement, the launch of the Euro, exhaustion of fossil fuel reserves, the impact of climate change.
-
∙ Unrealistic simplifying assumptions of behaviour, such as ignoring an individual’s flexibility to vary contribution rates in response to fund performance, flexibility of retirement date, interactions with other (non-pension) assets or liabilities.
-
∙ Government intervention. For example, in the extreme, savers face the risk that the government imposes a one-off flat rate tax on all pension savings above a certain level. Governments can also unpredictably vary the level of state pension provision and the extent to which this is means tested.
4.5. Financial Loss Protection and Environmental Protection: Mutual Learning
4.5.1. Background
Some of the introductory illustrations of the adverse consequences of model error and model risk have been drawn from other domains (the Millennium Bridge, the Tees Barrage). Here, we step briefly outside the worlds of insurance and finance to compare and contrast how model error and model risk are being addressed and managed elsewhere, in particular, in environmental protection and climate stabilisation. What, we enquire, does the world of finance have to learn from the world of environmental protection, and vice versa?
Over the half century or so in which computational models and foresight have been used in environment climate science, the presumption has largely been one of the truth of the matter eventually becoming capable of encapsulation in a model.Footnote 22 In the early days of systems ecology in the 1970s, for instance, a model of the behaviour of the flora and fauna in an aquatic ecosystem was being developed. It first appeared under the acronym CLEAN, and then CLEANER, with the strong suggestion that, should the model CLEANEST ever be produced (it was not), it would be the truth. Today, the presumption still endures: in that the current uncertainties in climate modelling could be resolved, if only one could have access to an ever larger computer (Palmer & Hardaker, Reference Palmer and Hardaker2011).
Indeed, there is a yet deeper (much deeper) guiding presumption: of there being a singular truth of the matter somewhere “out there” to be discovered. This is easy to suppose in a mature natural science, such as physics, with its laws of fluid mechanics, which underpin computational models of the movement of substances around the environment in space and time. It is a somewhat less straightforward premise to which to hold for modelling the interactions in an ecosystem among a host of chemical compounds; even more difficult, in respect of the many interacting biological species in an ecosystem; and even more difficult still, for the interactions among the individual organisms of each of those many species. And this – the existence of a singular truth of the matter – is clearly not something presumed necessarily to be the case in the businesses of insurance and banking.
4.5.2. Error and uncertainty in the model
That there is a discoverable, unique truth of the matter, and that models could be developed so as ultimately to encapsulate the utter and complete essentials of this truth, has long been the predominant paradigm in environment climate modelling. So much has it been so, in fact, that models of the behaviour of environmental systems have come to be referred to by some as “truth-generating machines”, albeit as a means (more recently) to illuminate the limitations of what has become known as Sound Science Analysis (SSA), to describe the construction and use of models at the science, policy, and society interfaces (Fisher et al., Reference Fisher, Pascual and Wagner2010; Wagner et al., Reference Wagner, Fisher and Pascual2010). Within this particular framework of policy making, the purpose of the model is to prove a regulation or ruling (of the US Environmental Protection Agency (EPA), for example) is supported by the soundest of science, with this being fully demonstrable in resolving challenges to such regulations in a court of law. Under SSA the model delivers detached, objective analysis. Uncertainty, while undesirable, is but a transient phenomenon. The burden of proof regarding the trustworthiness of the model rests upon the (in)security of the “Fidelity” of the model, for want of a better word (and to avoid several others, notably “Validity”Footnote 23 ). Accountability is measured by the proximity of the model to reality. Here Fidelity is gauged in terms of: (i) the match of the (external, output) behaviour of the model with observed behaviour (data) of the real thing; and (ii) the pedigree of the model’s internal mechanisms and workings (Funtowicz & Ravetz, Reference Funtowicz and Ravetz1990), itself measured as a function of (mono-disciplinary) scientific peer review of each of the (many) multi-disciplinary constituent pieces of knowledge (i.e. constituent hypotheses) of which the model is composed.
Troubled by the idea of models as truth-generating machines, legal scholars have expressed a preference for using them in an alternative Deliberative Problem Solving (DPS) framework for policy formation, wherein instead models facilitate deliberation, constructive contestation, and learning (as in Fisher et al., Reference Fisher, Pascual and Wagner2010). Uncertainty surrounding the model is taken to be an enduring phenomenon; it cannot be banished, eliminated, or ground into insignificance (by an ever larger, more complete model). As therefore in the models of finance and business, so too with models of the environment: some divergence between the model and that part of the world it is meant to simulate has to be tolerated. Under DPS, and as opposed to SSA, the model is viewed as a metaphor, an analogy, or a tool (Beck & Chen, Reference Beck and Chen2000). The burden of proof regarding the trustworthiness of the model rests now upon the quality of its design as a tool intended to fulfil a prescribed task, to which it may be well or ill-suited. In other words, quality about the design of the model (as a tool) has to do with its “materiality”, its “Fitness-for-Purpose”. In fact, Fitness-for-Purpose is quite the apt phrase for this present discussion (although it was not the phrase originally used in environmental science; see Beck & Chen, Reference Beck and Chen2000). Accountability under DPS is judged according to the effectiveness of problem solving.
These together, then – the SSA and DPS frameworks for using models for policy and decision making in environmental protection – mirror the US Federal Reserve’s (and our) definition of how model risk arises: because “[t]he model may have fundamental errors”, which errs towards the view of model error under SSA, and the model “may produce inaccurate outputs when viewed against the design objective and intended business uses”, which resonates more with how model error is viewed in the DPS framework. Differing frameworks on what constitutes the trustworthiness of a model may therefore co-exist in the same organisation. Indeed, the ways of judging quality in the design of a model for undertaking a specified task have been enriched, with measures of both Fidelity and Fitness-for-Purpose now applicable.
4.5.3. Using models and coming to a decision
These attributes – of the origins, nature, and occurrence of model error – are common to the domains of both finance and environment climate. The two domains also have perhaps surprisingly much in common when it comes to the nature and workings of the sociocultural milieu in which decisions are made. They are similar, therefore, in respect of how model risk arises from the second element of our definition of it: that “[t]he model may be used incorrectly or inappropriately” in coming to a decision.
In the abstract, at a “systems level”, the structures of the respective archetypal decisions to be made are largely identical. Both the environment and a company’s financial well-being need protection. A certain level of financial damage or a certain level of contamination of the environment should not be exceeded, with a given probability. In both instances, the respective regulator has an interest in not having such failures and losses and in using models to control the risk of their occurrence, hence the risk of model risk. In the worlds of both finance and the environment, proposed decisions may be hotly contested, and perhaps adjusted before they are eventually implemented. Some stakeholders will want to have the bar of potential environmental damage lowered, because the proposed restriction will undermine their company’s profitability. They fear their company will incur greater expenses in removing more of the contaminants associated with its commercial manufacturing and production processes. For like reasons of potentially impaired profits, some in the financial world will want their required capital reserves to be lowered. Others will wish to see precisely the opposite, however. The bars of capital reserves and environmental protection should be raised, they argue. In the case of the latter, this would typically be the stance of members of environmental activist groups, who may imagine all manner of catastrophes arising from even the smallest industrial contaminant release (very much in line, in other words, with those who hold to the “egalitarian” myth of nature in the lower-left quadrant of Figure 6).
There are important differences, however. In environmental protection, the regulator is wholly integrated in the processes of contestation and the procedures of governance – such as a court of law – for attaining an outcome from the (often-heated) debate. Stakeholders, that is, participants in the dispute, include the regulator therefore. The proposed decision, furthermore, is a direct function of the regulator’s model, not that of any (internal) model of some other stakeholder, for example, a business or professional association of similar businesses in similar economic sectors, whose commercial activities are about to be regulated. Significantly too, there will be those who, while they might otherwise put no trust in models at all (our “Uncertainty Avoiders” and “Intuitive Decision Makers” from section 3), will nevertheless have to put up with them and their use, precisely because the regulator has used them to develop the proposed decision. Their concern could well be that the model may be being used “incorrectly or inappropriately” by the regulator and/or the other industry stakeholders, who (unlike themselves) can afford the expertise necessary for running the model – and (worse still) tailor it to suit their own opposing argumentative purposes.Footnote 24 The concern of these cash-poor stakeholders is that the wool may be being pulled over their eyes. They rightly protest that the “black box” of the model should be opened up for all to scrutinise, for its mechanisms to be laid bare. So what they want, above all – perhaps indeed above either Fidelity or Fitness-for-Purpose in the design of the model – is “Transparency” about its inner workings. And that they should have this expectation has become more or less formally enshrined over the past quarter of a century in the guise of what is called “extended peer review” (Jasanoff, Reference Jasanoff1990; see also Funtowicz & Ravetz, Reference Funtowicz and Ravetz1990). All of those holding a stake in the outcome of the decision – especially those scientifically lay-stakeholders who are likely to bear the brunt of the actions (doings) following from the decision, and not merely the professional scientists with their scientific peer reviews – should be able to offer an opinion regarding the quality of the model in its design as the tool intended to undertake the assigned task.
Much the same repertoire of plural stances on the legitimacy and appropriate use of models in the decision process, as we now well know (from section 3), might be aired in the financial world. But the strict procedures and rules of a court of law (including those in respect of weights of evidence and opinion) will probably not be imposed on the contestation as a means of arriving eventually at a singular outcome from the dispute and debate. The debate, after all, takes place entirely within the one company, which is free to set its own terms of good governance for model risk management, including promoting, if not tolerating, a variety of modelling cultures (as our report has shown).
4.5.4. Vive la difference?
In March 2013, HM Treasury issued its Final Report on “Review of quality assurance of government analytical models” (referred to, in short, as HMT), to follow thus, in many ways, the Board of Governors of the Federal Reserve System, Office of the Comptroller of the Currency’s Supervisory Guidance on Model Risk Management (Report OCC 2011–22) issued on 4 April 2011 (and referred to as OCC). Both relate to the domain of finance, banking, and insurance.
In the domain of environmental protection, the closest equivalent of these two documents is the 2007 book Models in Environmental Regulatory Decision Making (National Academies Press) of the (US) National Research Council (referred to as NRC). The burden of its emphasis is on matters of statistical and computational technique, with a clear focus on model evaluation (previously labelled model “validation”). The study and research behind the NRC book were supported by the US EPA, whose decisions and rulings would often be subject to lawsuits, the outcomes of which might well turn on the answer to the question of “How valid is your model?”. And the expectation at the time was that this question would only be answered within the framework of SSA.
In contrast therefore to the OCC and HMT documents, whose burden of emphasis is placed much more squarely upon the sociocultural milieu of the people and procedure of model risk governance, the NRC book reflects a world of model-building and application in transition: from the overwhelming predominance of the SSA framework, in which getting the (single) model “correct” is uppermost; and towards circumstances in which the possibility of handling model error and uncertainty under the alternative DPS framework is beginning to be admitted. Crucial in this latter is tolerance of the view of a model as a tool for undertaking a prescribed task. In particular, as much of the purpose of building a model in the first place is to be able to generate and explore foresight about the behaviour of a system in the future that may be radically different from anything observed in the past, the struggle is to develop the logic and possibly some supporting quantitative measures of what amounts to higher (lower) quality in the design of a model for this task.Footnote 25 In a sense, and entirely in the spirit of the 1990 book by Funtowicz and Ravetz (on Uncertainty and Quality in Science for Policy), the outlook can be shifted from dwelling on the “downside” of uncertainty and error in a model to accentuating the “upside” of ever higher quality in its design.
Two chapters in the 2014 book Error and Uncertainty in Scientific Practice approach this challenge through the notion of key (critical) features of model uncertainty (identified from a special form of sensitivity analysis), relative to the coming to pass (or not) of the profoundly different future events and futures.Footnote 26 Both chapters deal with models in the fields of environment and climate. In one of them, support for the following argument is being canvassed: that coming to a view on quality in the design of the model is something rather subjective (as opposed to objective) – something that is in the “eye of the beholder”. And, of course, there can be plural sets of “eyes of beholders” – if a model has to be used in coming to a policy decision – just as there is a (fourfold) plurality of types of model users now acknowledged in the world of insurance and financial modelling, which brings us back to the issue of model risk governance, at the centre of this report: back, in other words, to the richness of variety of perspective on models, the quality of their design, and whether and how they should be used – and to the healthy (if noisy) contestation among these differing views – before finalising a decision.
“Culture”, even just the word itself, is important in the guidance on Model Quality Assurance (MQA) and Model Risk Management given in the HMT and OCC documents. It is code for governance. HMT, for instance, urges upon its audience (primarily Government departments) a culture wherein leaders value and recognise good MQA. Along with this should come a “no-blame” culture; a form of governance with transparency, one reflecting all the virtues of a “culture of learning from mistakes”. Such governance would facilitate “effective challenge” of the model – of the constructive, disputatious kind we are also advocating herein – and the avoidance of “group-think”. Avoiding group-think is clearly much on the mind of HMT. Significantly, HMT goes on to recommend a process of MQA that encourages “mutual understanding and respect … between policy and analytical professions”. In its own words:
“A diversity of backgrounds and experience in the team may help get the best out of individuals, helping teams to avoid group think and use individuals’ judgment effectively” (page 14; emphasis in original).
and again:
“Circumstances when teams should particularly consider external model audit include higher levels of risk arising from influence on critical decisions, particularly complex models, where there is concern over possible ‘group-think’ amongst those involved with the modelling, or where there have been recent changes in personnel, circumstances or model usage” (page 22).
Much of this is rounded off and reiterated in HMT’s “Conclusions and recommendations”:
“In particular, [stakeholders; Government departments] pointed to strong leadership from the top that values and expects effective challenge, a clear governance framework, and adequate time to allow expert and experienced staff to carry out quality assurance” (page 33).
In short, Model Risk is seen as a “Board-level risk” for HMT (consistent with our proposed Model Risk Management Framework, section 2.3); and an absence of healthy debate among contending views will not contribute to good governance in managing Model Risk, just as we are suggesting at the close of section 3.
4.6. Conclusion
This section focussed on model risk measurement and made attempts to quantify model risk, where possible.
In section 4.1 we said that to quantify model risk we needed to look at the effect of model risk on possible outcomes or decisions made using the model, and their financial impact. We looked at expected and unexpected model error for a variety of models, and mitigating actions. We said that model risk is not symmetric as there is little benefit from upside model risk, therefore model risk has option-like behaviour and could be quantified using techniques from option pricing.
Proxy modelling is the only example where model error can be precisely quantified. Quantification depends on rigorous OOS testing. In section 4.2, we stated that managing this type of model risk involves monitoring model error against a risk appetite relevant to the particular business lines being approximated, communicating the size of errors involved, and using this information in decision making, and taking action when the errors exceed the appetite.
We looked at irreducible model uncertainty in the context of longevity models in section 4.3, and concluded that forward-looking modelling should make heavy use of scenario testing of events not in the data to provide a reasonable range of future outcomes.
In section 4.4, we looked at applications to financial planning models. We explored the range of possible sources of model errors and compared the results of our tests with the stated confidence levels of meeting investment aims.
Lastly, in section 4.5 we stepped out of the world of financial models and found many similarities to the issues debated in the world of environmental protection models, on model errors and uncertainty, the use of models, and the need for a strong governance framework that focusses on identifying and mitigating model errors.
5. Summary Conclusions
Model risk arises from the use of quantitative models in decision making, which contain material errors or flaws, or from the inappropriate use of models. Model risk may involve human or programming errors, as demonstrated in the case studies of section 2.10 (for instance, the case of JPM’s “London Whale”). Alternatively, models invariably involve approximations and simplifications, which compromise the reliability of outputs, and may make their use inappropriate in particular applications, as was discussed in the context of proxy models in section 4.2. Finally, the statistical (and more broadly epistemic) uncertainty pertaining to complex quantitative models, such as the longevity models of section 4.3, makes it frequently challenging to ascertain the accuracy of a model’s outputs or even the range of likely error.
The case studies introduced in section 1 (and some elaborated on in section 2), demonstrate that the financial (and reputational) impacts of model risk can be very substantial.
Model risk can be managed through a Model Risk Management Framework as presented in section 2. We propose an enterprise-wide framework that fits all material models that an organisation uses, embraces thought leadership and best practice from recent market and regulatory developments, and applies sound risk management principles that are already embedded for more established risk types. Successful implementation of such a framework can avert losses from model risk such as those reported in case studies. In the current business environment, with decisions often informed by complex computational models, the Board and Senior Management expect that model outputs reported to them have been checked, that the models used to generate them are fully understood and validated, and that the materiality of possible model errors has been assessed. The Board is thus a fundamental stakeholder in the model risk management process.
Furthermore, we argued in section 3 that the complex processes leading to decisions in an organisation require us to consider carefully the different ways in which models are conceived within the organisation and used in decision making. We proposed a fourfold classification of attitudes to models and their uses, which may be encountered within an organisation. With arguments informed by the Cultural Theory of risk, originating in anthropology, we claim that each of those attitudes is a legitimate – but only partially appropriate – response to deep (model) uncertainties. The implication is drawn that model risk management must require feedback from and provide responses to a number of perspectives, going beyond purely technical model reviews. By additionally including operational and commercial considerations, reflecting the variety of cultures within the organisation, model risk management is enhanced. In fact, accepting the legitimacy of non-technical concerns regarding models, which are not always openly aired, helps preserve both the scientific integrity of modellers and the accountability of management. This discussion to an extent mirrors the debate around environmental models summarised in section 4.5, in particular the notion of an “extended peer community”.
In order to quantify the likely financial impacts of model risk, which is the task undertaken in section 4, one has to specify the ways in which model outputs drive decisions, such that model mis-specification translates into a suboptimal or dangerous decision. Given the complexity of actual decision processes, this is a material but necessary simplification. The possible ways in which model errors generate (adverse) financial impact in applications including pricing, hedging, and capital management, were discussed in section 4.1. The discussion reveals substantial complexities: for example, even when model errors are considered symmetrically distributed around a baseline, the financial impacts of model error are often biased in one particular (often adverse) direction. Furthermore, it is not always clear whether errors (e.g. in the calculated cost of capital) produce a true economic cost.
Different methods for the quantification of model risk are appropriate to different problems. In applications like proxy models (section 4.2), the key question is the appropriateness of an approximation to a more complex model. It is necessary to specify a model risk appetite relevant to the particular business lines being approximated, communicating the size of errors involved, and taking action when the measured errors exceed the risk appetite. On the other hand, in the case of irreducible model uncertainty, as in the example of longevity risk (section 4.3), it is necessary to employ a variety of measurement approaches, based on statistical inference, fitting multiple models, and stress and scenario analysis.
Substantial challenges remain. Model risk, although apparently a rather abstract concept, is pervasive, as it potentially undermines the tools themselves necessary for risk management. Furthermore, model risk is persistent, as even with the adoption of a comprehensive risk management framework and the use of best modelling practices, there will be important uncertainties that cannot be eliminated. The sensitivity of model outputs to contestable assumptions may be noted, but what can be done with that information? We tried to address this question through the discussion of governance and model cultures of section 3. However, the effectiveness of a governance response to (model) risk is contingent on the wider culture of the organisation: fundamentally the willingness to genuinely engage stakeholders with diverging views and to use governance processes to frame debate and generate challenge.
Finally, we identified through the report various areas that may merit deeper research. These include, but are not limited to:
-
1. Developing case studies to illustrate further how the concepts described in this Sessional Paper would work in practice. This would include, for some specific illustrative examples (both for actual observed, and emerging risk, scenarios), application of the materiality filtering process, quantification of the financial impact of model risk using stochastic models, assessment against a typical model risk-appetite statement, example model risk reporting, how the governance process might play out with all four model risk cultures represented as key stakeholders, and the consequential risk mitigation activities the company might take.
-
2. Further developing practical model risk governance responses, that make use of the plural rationalites (Cultural Theory) framework of section 3.
-
3. Systemic risk associated with the use of models, with a particular focus, for example, on the conjunction of circumstances in which use of essentially the same form of model by many market actors is allied with essentially identical decision-making procedures in the absence of the kinds of challenges illustrated in section 3 for the avoidance of group think.
-
4. More technically focussed research associated with model risk measurement, for instance, analysis of the sensitivity of asymmetric cost-benefit outcomes to the various sources of error embedded within a complex model.
Acknowledgements
We are grateful to Michael Thompson for his extensive advice and comments on the material presented in section 3.
We thank the audiences at the following conferences and events, where parts of the report were presented, for their valuable feedback: The IFoA CRO Group, London, 15 May 2014; IFoA Risk and Investment Conference, Glasgow, 1–3 June 2014; Annual Meeting of the Swiss Association of Actuaries, Davos, 5 September 2014; International Actuarial Association, London, 9 September 2014; Financial Stability Seminar, Bank of England, London, 13 October 2014; ORIC, London, 26 November 2014; IFoA Life Conference, Birmingham, 9–11 November 2014.















