Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:14:38.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Ruin Probability During A Finite Time Interval

Published online by Cambridge University Press:  29 August 2014

R. E. Beard
R. E. Beard*
Affiliation:
University of Essex
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper was inspired by comments by H. L. Seal in a series of lectures given to the Actuaries Club in New York and by a paper of his recently published in the Swiss Actuarial Journal (Seal, 1972 [6]). In his lectures he showed that the probability U(w, t) that a risk reserve at every epoch τ, where o < τ ≤ t will be non negative when the initial risk reserve is w is related to 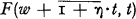, the probability that the aggregate claim outgo through epoch t does not exceed 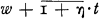by the relationship

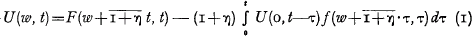
where η is the security loading and f(x, t) = (∂/∂x) F(x, t).

It is assumed that the d.f. F(x, t) is differentiable eith regard to x with a possible exception at the point x = o.

Using an extension of the “ballot theorem” in Chapter III of Feller (1968 [4]) he showed that 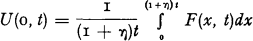and observed that if numerical values of F(x, t) were available values of U(w, t) could be computed.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 8 , Issue 3 , September 1975 , pp. 265 - 271
Copyright
Copyright © International Actuarial Association 1975

References

[1]Amos, D. F. and Daniel, S. L. (1971), Tables of Percentage Points of Standardised Pearson Distributions, Sandia Research Report, SC-RR-0348.Google Scholar
[2]Bohman, H.and Esscher, F.(1964), Studies in Risk Theory with Numerical Illustrations, Concerning Distribution Functions and Stop Loss Premiums, Skand. Aktu. Tidskr., 46.Google Scholar
[3]Bromwich, T.J. I'a (1947), An Introduction to the theory of Infinite Series, 2nd Ed., MacMillan, London.Google Scholar
[4]Feller, W.(1968), An Introduction to Probability Theory and its Applications, Vol.I, Wiley, New York.Google Scholar
[5]Pearson, K.(1922), Tables of the Incomplete Γ-function, Cambridge University Press.CrossRefGoogle Scholar
[6]Seal, H. L. (1972), “Numerical calculation of the probability of ruin in the Poisson/Exponential case”, Mitt. Verein. Schweiz. Versich. Mathr., 72, 77–100.Google Scholar