Article contents
A Pricing Model in a Sensitive Insurance Market
Published online by Cambridge University Press: 29 August 2014
Extract
A great attention has been devoted, in the actuarial literature, to premium calculation principles and it has been often emphasized that these principles should not only be defined in strictly actuarial terms, but should also take into account the market conditions (Bühlmann (1980), de Jong (1981)).
In this paper we propose a decision model to define the pricing policy of an insurance company that operates in a market which is stratified in k risk classes 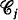 .
.
It is assumed that any class constitutes a homogeneous collective containing 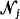 independent risks Sj(t) of compound Poisson type, with the same intensity λj. The number nj of risks of
independent risks Sj(t) of compound Poisson type, with the same intensity λj. The number nj of risks of 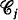 that are held in the insurance portfolio depends on the premium charged to the class by means of a demand function which captures the concept of risk aversion and represents the fraction of individuals of
that are held in the insurance portfolio depends on the premium charged to the class by means of a demand function which captures the concept of risk aversion and represents the fraction of individuals of 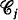 , that insure themselves at the annual premium xj.
, that insure themselves at the annual premium xj.
With these assumptions, the return Y on the portfolio is a function of the vector x = (x1, x2, …, xk) of the prices charged to the single classes (and of the time) and x is therefore the decision policy instrument adopted by the company for the selection of the portfolio, whose optimal composition is evaluated according to a risk-return type performance criterion.
As a measure of risk we adopt the ultimate ruin probability q(w) that, in the assumptions of our model, can be related to a safety index τ, by means of Lundberg-de Finetti inequality. Even though it has been widely debated in the actuarial field, the use of q(w) offers undeniable operational advantages. In our case the safety index τ can be expressed as a function of x and therefore, in the phase of selecting an efficient portfolio, it becomes the function to be maximized, for a given level M of the expected return.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1982
References
REFERENCES
- 2
- Cited by


