Article contents
Minimum Variance Reinsurance*)
Published online by Cambridge University Press: 29 August 2014
Extract
In a paper entitled “An Attempt to Determine the Optimum Amount of Stop Loss Reinsurance” (XVIth Int. Congr. Act. Bruxelles 1960) Karl Borch has shown that, if the reinsurance premium is given, the smallest variance of the cedent's payments is obtained by a stop-loss reinsurance contract. Paul Markham Kahn, in “Some Remarks on a Recent Paper by Borch”, a paper read to the 1961 Astin Colloquium, has given an elegant proof of this theorem which appears to apply also to cases not considered by Borch. In this paper we study the problem from the reinsurer's point of view and it will be seen that, under natural conditions which are also used in the proof of the Borch-Kahn theorem, the minimum variance of the reinsurer's payments is obtained by a quota contract. This focusses attention on a peculiar opposition of interests of the two partners of a reinsurance contract. However, we do not enter any further into the investigation of a possible resolution of this conflict.
We study a problem concerning the division of risk between a cedent and his reinsurer. The risk may refer to a whole portfolio (in which case one might consider a Stop-Loss contract), or to a single contract (when an Excess-Loss contract is a possibility). We shall here use the nomenclature of a portfolio reinsurance.
Let it be assumed that a function F(x) is known which gives the probability of a total claim not exceeding x. We have then in Stieltjes integral notation
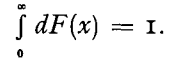
The two partners to a reinsurance arrangement agree that the reinsurer reimburses m(x).x out of a claim of x, where m(x) is a continuous and differentiate function of x and o ≤ m(x) ≤ 1.
- Type
- Papers
- Information
- Copyright
- Copyright © International Actuarial Association 1962
Footnotes
Paper presented to the Rättvik Colloquium 1961.
References
*) Paper presented to the Rättvik Colloquium 1961.
- 31
- Cited by


