Article contents
Largest Claims Reinsurance (LCR). A Quick Method to Calculate LCR-Risk Rates from Excess of Loss Risk Rates
Published online by Cambridge University Press: 29 August 2014
Extract
Let us denote by E(x) the pure risk premium of an unlimited excess cover with the retention x and by H(x) and m(x) the corresponding expected frequency and severity.
We thus have E(x) = H(x) · m(x).
H(x) is a non-increasing function of x and for practical purposes we can assume that it is decreasing; H′(x) < o. The equation H(x) = n has then only one solution xn, where n is a fixed integer.
Let En denote the risk premium for a reinsurance covering the n largest claims from the bottom.
Let us define 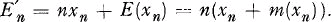 Intuitively we feel that
Intuitively we feel that 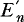 is a good approximation for En.
is a good approximation for En.
We shall first show that when the claims size distribution is Pareto and the number of claims is Poisson distributed, 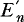 is a good approximation for En, being slightly on the safe side. We further include a proof given by G. Ottaviani that the inequality
is a good approximation for En, being slightly on the safe side. We further include a proof given by G. Ottaviani that the inequality 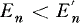 always holds.
always holds.
In the Pareto case we have
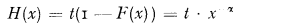
where the Poisson parameter t stands for the expected number of claims in excess of 1 (equal to a suitably chosen monetary unit) and
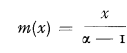 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1978
References
- 20
- Cited by


