Published online by Cambridge University Press: 29 August 2014
It has been known for generations that the fire risk rate increases with the size of the insured object in a similar way as the death rate increases with the age.
Professor d'Addario and other Italian mathematicians have shown that statistical data often can be graduated by the formulas where S denotes the sum insured:
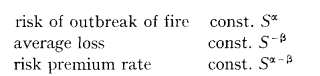
In 1940, d'Addario) in a practical case found the values α = 0.78, β = 0.44. In 1956, Blandin and Depoid have used the same formulas. Although these formulas in practical cases often lead to good approximations, one can hardly say that a proper mathematical or physical model describing the behaviour of fires lies behind.
About 1950, I worked with the statistics of a group of Danish fire insurance companies, in particular covering farm buildings. This investigation was organized by Gunnar Benktander. Our data confirmed the increase of the fire risk rate with the size of the buildings.
In one special group: Farm houses with thatched roofs, this increase was so important that the risk premium was approximately proportionate to the square of the sum insured. The statistics fully justified the tariffing and we tried to construct a model describing and explaining the observed facts.
The risk group in question was characterized by the overwhelming importance of total or practically total losses. Only a few per cent of the damages went to minor fires. When a fire breaks out in such a building, and reaches a certain slight extent, then it is not possible to save the building from total destruction. With sufficient approximation, we may say that only total losses occur (as in life assurance).
Presented at the 14th ASTIN Colloquium, Taormina, October 1978.
1 Annali dell' Istituto di Statistica, Vol. 17, Bari, 1940.
2 Hilary Seal in Survival Probabilities (Wiley 1978), shortly mentions Barrois' work.