Distributions des sinistres incendie selon leur coût

Extract

On peut penser que la dimension des sinistres est la résultante d'un très grand nombre de causes indépendantes à effets positifs.

Soient

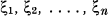
les variables aléatoires indépendantes qui représentent les facteurs élémentaires exerçant leur action dans l'ordre indiqué par les indices.

Si X_ν est l'ampleur du sinistre dû aux facteurs ξ₁, ξ₂, …., ξ_ν nous pouvons supposer que l'augmentation causée par ξ_ν+1 soit proportionelle à ξ_ν+1 et à une certaine fonction, g(X_ν) de la dimension X_ν.

C'est à dire, nous supposons qu'il y ait les relations:

Si chaque facteur n'apporte qu'un faible contribut à l'augmentation du sinistre, nous pouvons alors poser approximativement aussi:

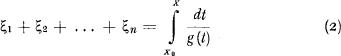
Comme X varie de X_o à X_n (et que X = X_n désigne la dimension extrème du sinistre) le second membre de la (2) décrit une variable aléatoire, fonction de X.

Puisque par hypothèse ξ₁,, ξ₂, …., ξ_n sont des variables aléatoires indépendante, si n est suffisament grand, d'après le théorème de la limite des probabilités il s'insuit que la variable aléatoire au second membre de la (2), est, à la limite, distribuée suivant la loi normale. Si l'on pose g(t) = t − c, la variable aléatoire normale qui décrit la dimension du sinistre pourra être posée dans la forme In(X − c).