I. INTRODUCTION
Digital fingerprinting technique enables us to trace illegal users from a pirated copy. It involves the distribution of multimedia content to legitimate users, embedding of user-specific identity information, and identification of illegal users. The assistant with cryptographic techniques and watermarking techniques is inevitable to realize a secure and robust fingerprinting system.
One of the important issues for fingerprinting technique is the dispute between buyer and seller. If both the buyer and seller obtain fingerprinted content in the transaction between them, the seller cannot prove to the other party that a pirated copy comes from the buyer. As the seller will be able to distribute the copy by himself to frame an innocent buyer, an illegal user will repudiate by claiming that the copy is created by the seller. By introducing cryptographic techniques in the transaction in [Reference Pfitzmann and Schunter1], a fingerprinting system assures an asymmetric property such that only a buyer can obtain uniquely fingerprinted content.
The original idea of the asymmetric system is to exploit the homomorphic property of a public-key cryptosystem that enables a seller to embed an encrypted fingerprint in encrypted content. Since the ciphertext is computed using a buyer's public key, only the buyer can decrypt it; hence, only he can obtain the fingerprinted content. It is also desirable for the fingerprinting system to solve the unbinding problem such that the relation between fingerprint information and a specific transaction performed by a buyer and a seller can not be retrieved [Reference Lei, Yu, Tsai and Chan2].
From the different point of view, the threat in a fingerprinting system is the collusion among users. Because differently fingerprinted versions of the same content are delivered to users, two or more users may collude to modify/delete the fingerprint. A fingerprinting code is a carefully selected collection of codewords that enables a seller to catch at least one illegal user. Among some fingerprinting codes, a bias-based code proposed by Tardos [Reference Tardos3] shows a minimum order of its code length. There are a variety of investigations about the Tardos code including the revision of bias probabilities [Reference Nuida4,Reference Laarhoven and Weger5] and tracing algorithm [Reference Škorić, Katzenbeisser and Celik6], design of threshold [Reference Cérou, Furon and Guyader7], and so on. In [Reference Charpentier, Fontaine, Furon and Cox8], the Tardos code is applied in an asymmetric fingerprinting system by using an oblivious transfer and commutative encryption scheme. Although it can eliminate a trusted center in the system, a judge needs secret parameters of the fingerprinting code and illegal users must participate in the tracing protocol.
In this paper, we propose a new tracing protocol by introducing an idea of delegated server. The server helps a seller to identify illegal users when a pirated copy is found. In the proposed protocol, a trusted center selects secret parameters of fingerprinting code, and issues each codeword to each user. The center sends ciphertexts of weighting parameters so that in an encrypted domain the seller can calculate a level of suspicion for each user by means of correlation of codewords at the tracing protocol. The delegated server decrypts the ciphertext of such a correlation score and returns a binary decision for each ciphertext. The leakage of information about secret parameters in the system is well-controlled by using cryptographic techniques and restrictions at the requests from the seller. We also measure the required computational resources in the proposed system.
The advantages of the proposed system are the following two points:
1) A trusted center's task is to issue secret parameters at the initialization phase.
2) A trusted center and illegal users need not to participate in the tracing protocol.
After the identification of illegal users, the seller can claim the fact to a judge by showing collected proofs.
The rest of this paper is organized as follows. In Section II, we briefly review an additive homomorphic encryption scheme and fingerprinting techniques including the cryptographic protocol and collusion secure fingerprinting code. In Section III, we propose a decentralized tracing protocol by introducing a delegated server. The security of the proposed scheme is discussed in Section IV, and the experimental results are shown in Section V. In Section VI, we discuss about the extension toward optimal scoring function. Finally, the conclusions are made in Section VI.
II. PRELIMINARIES
A) Homomorphic encryption
Let m 1 and m 2 be plaintexts. A homomorphic enciphering function E() satisfies the following property:
where f() is an arithmetic operation such as addition, multiplication, exclusive-or and, so on. For instance, it is multiplication in the RSA cryptosystem [Reference Rivest, Shamir and Adleman9]. Among some homomorphic encryption schemes, the additive homomorphism of Paillier's cryptosystem has attracted many researchers. It allows us to perform the following two operations in an encrypted domain.
The Paillier cryptosystem [Reference Paillier10] encrypts a plaintext m to obtain a ciphertext C by mapping ℤn to ![]() ${\open Z}^{\ast}_{N^2}$, where N is a composite of two large primes similar to the RSA cryptosystem.
${\open Z}^{\ast}_{N^2}$, where N is a composite of two large primes similar to the RSA cryptosystem.
• Key generation
According to a security parameter, two large primes P and Q are selected, and its product N = PQ is calculated. The Carmichael's function is used to calculate λ = lcm(P − 1, Q − 1). A generator g is selected from
 ${\open Z}^{\ast }_{N^2}$. The public key is (N, g) and the secret key is λ.
${\open Z}^{\ast }_{N^2}$. The public key is (N, g) and the secret key is λ.• Encryption
A ciphertext C is calculated from a plaintext m by using a random number r ∈ ℤN as follows:
(4) $$ C = E(m, r) = g^m r^N \bmod N^2 $$
$$ C = E(m, r) = g^m r^N \bmod N^2 $$• Decryption
If C < N 2, then the plaintext can be calculated as follows:
(5)where L(x) = (x − 1)/N. $$ D(C) = \displaystyle{{L(C^\lambda \bmod N^2)}\over{L(g^\lambda \bmod N^2)}} \bmod N, $$
$$ D(C) = \displaystyle{{L(C^\lambda \bmod N^2)}\over{L(g^\lambda \bmod N^2)}} \bmod N, $$
For the security reason, the size of N should be more than 1024 bits to assure that the factoring the composite is sufficiently difficult in a realistic computational resources. In a RSA cryptosystem, it is recommended to use 2048 bit modulus, and hence, the ciphertext size of Paillier cryptosystem is 4096 bits in such a case though the plaintext size is 2048 bits.
B) Cryptographic protocol
In [Reference Pfitzmann and Sadeghi11–Reference Kuribayashi and Tanaka15], the asymmetric property is realized by using the homomorphic property of public-key cryptosystems. It enables a seller to embed fingerprint in multimedia content in an encrypted domain. The fingerprinting system composed of protocols such as initialization protocol, purchase protocol, and tracing protocol.
Lei et al. [Reference Lei, Yu, Tsai and Chan2] considered the unbinding problem such that the relation between fingerprint information and a specific transaction performed by a buyer and a seller cannot be retrieved. On the other hand, Pfitzmann et al. [Reference Pfitzmann and Sadeghi11,Reference Pfitzmann and Sadeghi12] introduced the digital cash scheme to a fingerprinting protocol, and Camenisch [Reference Camenisch13] used group signature schemes for the solution of the unbinding problem.
The protocols in [Reference Lei, Yu, Tsai and Chan2] introduced a trusted authority who generates a robust fingerprint when valid items of a certain transaction between a buyer and a seller are transmitted from the seller. In [Reference Kuribayashi and Tanaka15,Reference Deng, Bianchi, Piva and Preneel16], the enciphering rate is improved using a public-key cryptosystem with an additive homomorphism [Reference Paillier10] by packing several bits in one ciphertext.
Although the homomorphic property is effective for constructing the asymmetric purchase protocol, the protocol incurs heavy computational costs. The efficiency of the transaction between a seller and buyer must be considered for a real-time distribution over the network. Although complicated cryptographic protocols are required to assure a sufficiently high security level, the computational cost must be reasonably small. In [Reference Kuribayashi and Tanaka17], the asymmetric property is satisfied by managing the decryption keys issued to users, which enables us to use a symmetric cryptosystem like advanced encryption standard (AES). In [Reference Ferrer and Megías18], a P2P protocol for distributed multicast of fingerprinted content is proposed by combining cryptographic primitives and robust watermarking. The protocol is improved by introducing an idea of recombination mechanism in a P2P-based distribution scenario in [Reference Megías and Ferrer19]. Its tracing algorithm is simplified into a simple and efficient database search in [Reference Megías20]. By using a discretized bias-based fingerprinting code [Reference Nuida4] in [Reference Megías and Qureshi21], the tracing protocol is developed in an encrypted domain, protecting the privacy of all users except for illegal users.
C) Fingerprinting code
A fingerprinting code has been investigated to solve the problem of collusion attacks such that a coalition of users called colluders compares the differences among their copies and tries to modify/delete the embedded fingerprint. Boneh and Shaw [Reference Boneh and Shaw22] presented the first construction of a fingerprinting code under a well-known marking assumption. The marking assumption enforces colluders to produce a pirated codeword so that they cannot change the symbols of codeword at the positions where all of their symbols are identical.
Among some fingerprinting codes, Tardos [Reference Tardos3] proposed a bias-based code which code length is theoretically minimum order. Let N u be the number of users in a system and ℓ be the code length. The code length ℓ can be determined both by the number of users N u in a system and maximum number c max of colluders assumed at the setting of code. A binary codeword of j-th user is denoted by X j,i ∈ {0, 1}, (1 ≤ j ≤ N u, 1 ≤ i ≤ ℓ), where X j,i is generated from an independently and identically distributed random number with a probability p i such that ![]() $\Pr [X_{j,i}=1]=p_i$ and
$\Pr [X_{j,i}=1]=p_i$ and ![]() $\Pr [X_{j,i}=0]=1-p_i$. This probability p i in the Tardos code follows a probability distribution
$\Pr [X_{j,i}=0]=1-p_i$. This probability p i in the Tardos code follows a probability distribution ![]() ${\cal P}$ over an open unit interval (0, 1), which is called bias distribution. Due to the use of such a bias, it is called bias-based fingerprinting code.
${\cal P}$ over an open unit interval (0, 1), which is called bias distribution. Due to the use of such a bias, it is called bias-based fingerprinting code.
Suppose that a pirated codeword y i, (1 ≤ i ≤ ℓ) is produced by colluders with a certain collusion strategy. The tracing algorithm of Tardos code calculates a similarity of codeword extracted from a pirated copy with candidates. The similarity is calculated by the correlation score S j which is the sum of each piece S j,i for each element y i of codeword with length ℓ.
 $$ S_j = \sum_{i=1}^{\ell}S_{j,i} = \sum_{i=1}^{\ell}y_iU_{j,i}, $$
$$ S_j = \sum_{i=1}^{\ell}S_{j,i} = \sum_{i=1}^{\ell}y_iU_{j,i}, $$where
 $$U_{j,i} = \left\{ {\matrix{ {-\sqrt {\displaystyle{{p_i} \over {1-p_i}}} } \hfill & {{\rm if}\; X_{j,i} = 0} \hfill \cr {\sqrt {\displaystyle{{1-p_i} \over {p_i}}} } \hfill & {{\rm if}\; X_{j,i} = 1} \hfill \cr } } \right..$$
$$U_{j,i} = \left\{ {\matrix{ {-\sqrt {\displaystyle{{p_i} \over {1-p_i}}} } \hfill & {{\rm if}\; X_{j,i} = 0} \hfill \cr {\sqrt {\displaystyle{{1-p_i} \over {p_i}}} } \hfill & {{\rm if}\; X_{j,i} = 1} \hfill \cr } } \right..$$If a correlation score of a codeword assigned to a user exceeds a certain threshold Z, the user is detected as guilty.
The original tracing algorithm only uses a half of information from a pirated copy because the value of the score S j,i becomes zero when y i = 0. In order to utilize the whole information, ![]() $\breve {\rm S}$korić et al. [Reference Škorić, Katzenbeisser and Celik6] proposed a symmetric version of the scoring function.
$\breve {\rm S}$korić et al. [Reference Škorić, Katzenbeisser and Celik6] proposed a symmetric version of the scoring function.
D) Problem in tracing protocol
In the above conventional systems, when a pirated copy is discovered, a seller first extracts the fingerprinting codeword, and then requests a trusted center to identify colluders. The center calculates correlation scores for all users registered in a system, and identifies colluders whose score exceeds a threshold. As such an operation at the center requires heavy computational resources, we consider a load dispersion at the tracing protocol. However, the secrecy of parameters in a fingerprinting code must be considered in the protocol. Once users' codewords X j,i are leaked to a malicious seller, innocent users may be accused from fake content distributed by the seller because he can produce a specific fingerprinted version of content by his choice. On the contrary, without X j,i the score ![]() $S^{sym}_j$ cannot be calculated. In a similar reason, the bias probability p i is also important parameter in the tracing protocol.
$S^{sym}_j$ cannot be calculated. In a similar reason, the bias probability p i is also important parameter in the tracing protocol.
III. DECENTRALIZED TRACING PROTOCOL
A trusted center delegates authority to a server in the proposed system. Once a seller finds a pirated copy, he calculates the correlation score ![]() $S^{sym}_j$ of j-th user in an encrypted domain by using the extracted codeword y i and encrypted U j,i, (1 ≤ l ≤ ℓ). The seller requests the server whether the user is guilty or not by sending the ciphertext of
$S^{sym}_j$ of j-th user in an encrypted domain by using the extracted codeword y i and encrypted U j,i, (1 ≤ l ≤ ℓ). The seller requests the server whether the user is guilty or not by sending the ciphertext of ![]() $S^{sym}_j$.
$S^{sym}_j$.
The important parameters in the proposed system are summarized in Table 1.
Table 1. Important parameters in the fingerprinting system.

A) Delegated authority
A delegated server generates a public key and secret key pair of the Paillier cryptosystem, and registers the public key at a public key infrastructure (PKI). In order to ensure its independency, the trusted center does not know the secret key.
The trusted center allows the server to check a correlation score whether it exceeds a threshold which is determined by the center. The server is blind to the setting of fingerprinting code except for the threshold and the number c max. The server's task is to decrypt a ciphertext received from a seller, and return a binary decision.
The role of server is regarded as a decryption oracle which receives a ciphertext and returns the decryption result. As discussed in cryptographic community, the number of queries to the server should be limited for a security reason. The more queries a seller requests, the more information about X j,i and p i he obtains. As there are many users, the seller requests multiple ciphertexts simultaneously to find suspicious users whose score ![]() $S^{sym}_j$ exceeds the threshold Z. In order to manage the information leakage, three restrictions are introduced into the check at the server.
$S^{sym}_j$ exceeds the threshold Z. In order to manage the information leakage, three restrictions are introduced into the check at the server.
One is the number of ciphertexts at each request which must be equal to the number of users in a system. Due to the limitation of traceability in a fingerprinting code, the number of suspicious users must be less than c max. If the number of the scores exceeding the threshold is more than c max, the server rejects the request. This is the second restriction. The third one is the statistical distribution of scores. It is known that the scores of innocent users follows Gaussian distribution with zero means [Reference Škorić, Vladimirova, Celik and Talstra23,Reference Furon, Guyader and Cérou24]. Except for a few scores of colluders, the scores observed after the decryption of requested ciphertexts must follow the distribution. Hence, a server checks the soundness of the request by the above three restrictions.
B) Initialization
There are four parties in the system, trusted center, delegated server, seller, and buyer(user). The procedure is illustrated in Fig. 1.
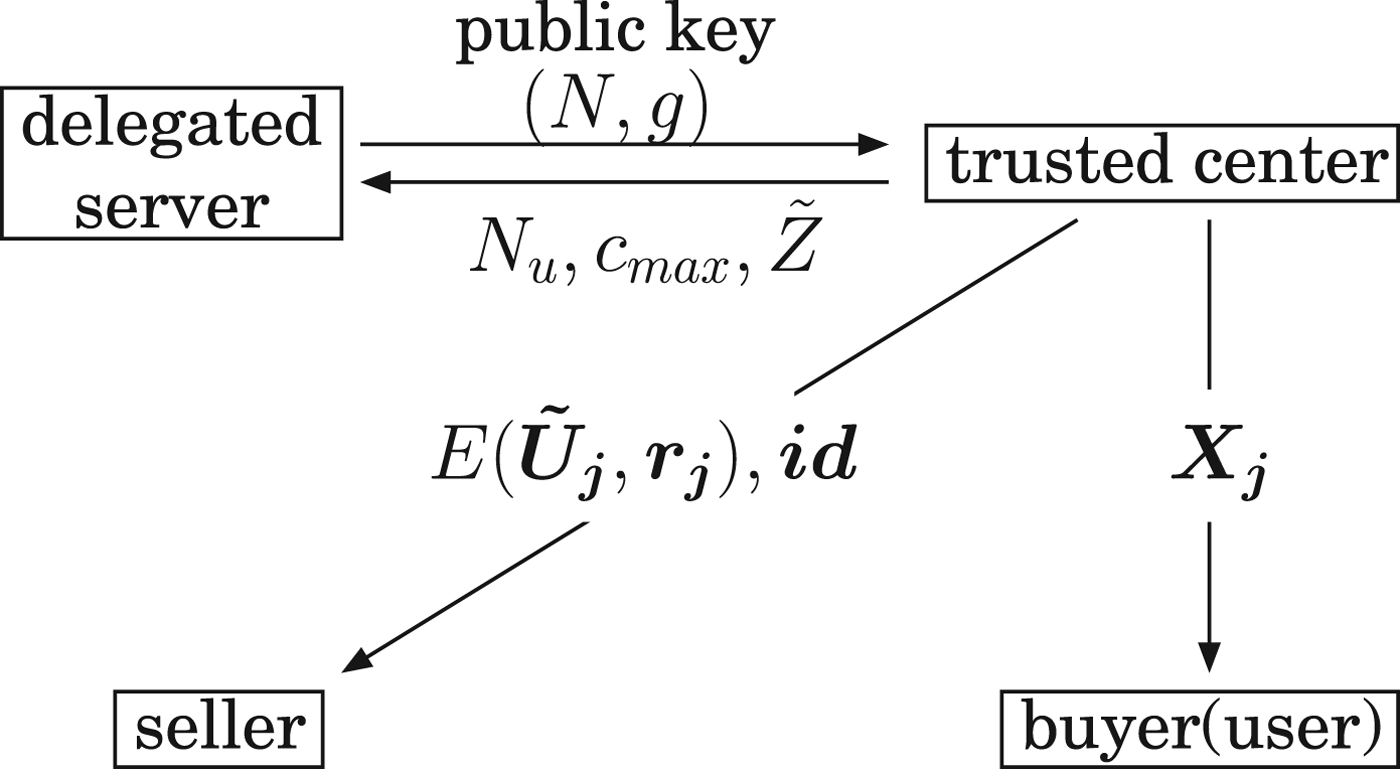
Fig. 1. Illustration of initialization phase. After the initialization, a trusted center need not to participate in a tracing protocol.
A trusted center selects a security parameter to generate parameters such as c max and p i, (1 ≤ i ≤ ℓ) of a fingerprinting code, and issues a codeword ![]() $\vec {\bi X}_j$ to j-th user whose ID information is id j. Then, the weighting parameters U j,i are calculated for the codeword
$\vec {\bi X}_j$ to j-th user whose ID information is id j. Then, the weighting parameters U j,i are calculated for the codeword ![]() $\vec {\bi X}_j$.
$\vec {\bi X}_j$.
The trusted center gets the public key of a delegated server. Remember that a plaintext in the Paillier cryptosystem is an element in an integer finite field ℤN. In order to encrypt U j,i, (1 ≤ i ≤ ℓ), the center first multiplies a scaling parameter α to scale up its small number, and then, rounds the value into a nearest integer using a round function round().
Finally, the center encrypts ![]() $\tilde {U}_{j,i}$ by using a random number r j,i.
$\tilde {U}_{j,i}$ by using a random number r j,i.
In the conventional studies [Reference Tardos3,Reference Škorić, Katzenbeisser and Celik25], the weighting parameters U j,i are stored as a two-dimensional array, and one of two values is selected according to X j,i ∈ {0, 1}. On the other hand, we make one ciphertext ![]() $E(\tilde {U}_{j,i},\, r_{j,i})$ from i-th element of codeword X j,i for 1 ≤ i ≤ ℓ. Hence, ℓ ciphertexts
$E(\tilde {U}_{j,i},\, r_{j,i})$ from i-th element of codeword X j,i for 1 ≤ i ≤ ℓ. Hence, ℓ ciphertexts ![]() $E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ are generated for each user.
$E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ are generated for each user.
The trusted center sends a list of ciphertexts ![]() $E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ and the corresponding ID information
$E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ and the corresponding ID information ![]() $\vec {\bi id}=(id_1,\, \ldots ,\, id_{N_u})$ to a seller. When the number of users is N u, the total number of ciphertexts is N uℓ, which is transmitted to the seller from the center.
$\vec {\bi id}=(id_1,\, \ldots ,\, id_{N_u})$ to a seller. When the number of users is N u, the total number of ciphertexts is N uℓ, which is transmitted to the seller from the center.
A threshold ![]() $\tilde {Z}$ is calculated from
$\tilde {Z}$ is calculated from ![]() $\tilde {U}_{j,i}$ by using the probabilistic algorithm [Reference Cérou, Furon and Guyader7] which can estimate very low probability of error. The trusted center informs N u, c max and
$\tilde {U}_{j,i}$ by using the probabilistic algorithm [Reference Cérou, Furon and Guyader7] which can estimate very low probability of error. The trusted center informs N u, c max and ![]() $\tilde {Z}$ to the server.
$\tilde {Z}$ to the server.
C) Tracing protocol
After the above setup, a certain secure fingerprinting protocol is executed between a seller and each user. Then, each user obtains a fingerprinted copy containing his codeword ![]() $\vec {\bi X}_j$. Suppose that a coalition of malicious users produce a pirated copy, and the seller finds the copy at somewhere.
$\vec {\bi X}_j$. Suppose that a coalition of malicious users produce a pirated copy, and the seller finds the copy at somewhere.
First, the seller tries to extract a codeword from the pirated copy. Let ![]() $\vec {\bi y}=(y_1,\, \ldots ,\, y_{\ell })$, y i ∈ {0, 1} be the codeword. Then, a scaled correlation score
$\vec {\bi y}=(y_1,\, \ldots ,\, y_{\ell })$, y i ∈ {0, 1} be the codeword. Then, a scaled correlation score ![]() $\tilde {S}^{sym}_j$ for each user is calculated in an encrypted domain under the modulus N 2 using an encrypted weighting parameters
$\tilde {S}^{sym}_j$ for each user is calculated in an encrypted domain under the modulus N 2 using an encrypted weighting parameters ![]() $E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ for 1 ≤ j ≤ N u:
$E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ for 1 ≤ j ≤ N u:
 $$\matrix{ {\prod\limits_{i = 1}^\ell E {({\tilde{U}}_{j,i},r_{j,i})}^{2y_i-1}} \hfill & { = E\left( {\sum\limits_{i = 1}^\ell {(2y_i-1)} {\tilde{U}}_{j,i},r_{j,i}^{\prime} } \right)} \hfill \cr {} \hfill & { = E\left( {\tilde{S}_j^{sym} ,r_j^{\prime} } \right),} \hfill \cr } $$
$$\matrix{ {\prod\limits_{i = 1}^\ell E {({\tilde{U}}_{j,i},r_{j,i})}^{2y_i-1}} \hfill & { = E\left( {\sum\limits_{i = 1}^\ell {(2y_i-1)} {\tilde{U}}_{j,i},r_{j,i}^{\prime} } \right)} \hfill \cr {} \hfill & { = E\left( {\tilde{S}_j^{sym} ,r_j^{\prime} } \right),} \hfill \cr } $$where ![]() $r^\prime _{j,i} = r^{2y_i-1}_{j,i} \bmod N$ and
$r^\prime _{j,i} = r^{2y_i-1}_{j,i} \bmod N$ and ![]() $r^\prime _j=\sum r^\prime _{j,i} \bmod N$. It is noted that
$r^\prime _j=\sum r^\prime _{j,i} \bmod N$. It is noted that ![]() $\tilde {S}^{sym}_j \approx \alpha S^{sym}_j$ if α is sufficiently large from equation (9).
$\tilde {S}^{sym}_j \approx \alpha S^{sym}_j$ if α is sufficiently large from equation (9).
The seller sends the ciphertexts ![]() $E(\tilde {S}^{sym}_j,\, r^\prime _j)$, (1 ≤ j ≤ N u) to the server. The server decrypts the ciphertexts and checks the scores. If the number of the scores satisfying the condition
$E(\tilde {S}^{sym}_j,\, r^\prime _j)$, (1 ≤ j ≤ N u) to the server. The server decrypts the ciphertexts and checks the scores. If the number of the scores satisfying the condition ![]() $\tilde {S}^{sym}_j > \tilde {Z}$ is more than c max, the server rejects the request. Otherwise, the indices of the scores satisfying the condition are sent to the seller. Namely, the server calculates the following indices
$\tilde {S}^{sym}_j > \tilde {Z}$ is more than c max, the server rejects the request. Otherwise, the indices of the scores satisfying the condition are sent to the seller. Namely, the server calculates the following indices ![]() $\vec {\bi I}$:
$\vec {\bi I}$:
where
and ![]() $\vert \vec {\bi I} \vert \le c_{max}$. Finally, the statistical distribution of
$\vert \vec {\bi I} \vert \le c_{max}$. Finally, the statistical distribution of ![]() $\tilde {S}^{sym}_j$ is measured whether it follows Gaussian. According to the indices
$\tilde {S}^{sym}_j$ is measured whether it follows Gaussian. According to the indices ![]() $\vec {\bi I}$, the seller can identify the illegal users as the results. It is noted that the number of requests to a delegated server is limited. It is because of the security reason explained at next section. The above protocol is illustrated in Fig. 2.
$\vec {\bi I}$, the seller can identify the illegal users as the results. It is noted that the number of requests to a delegated server is limited. It is because of the security reason explained at next section. The above protocol is illustrated in Fig. 2.
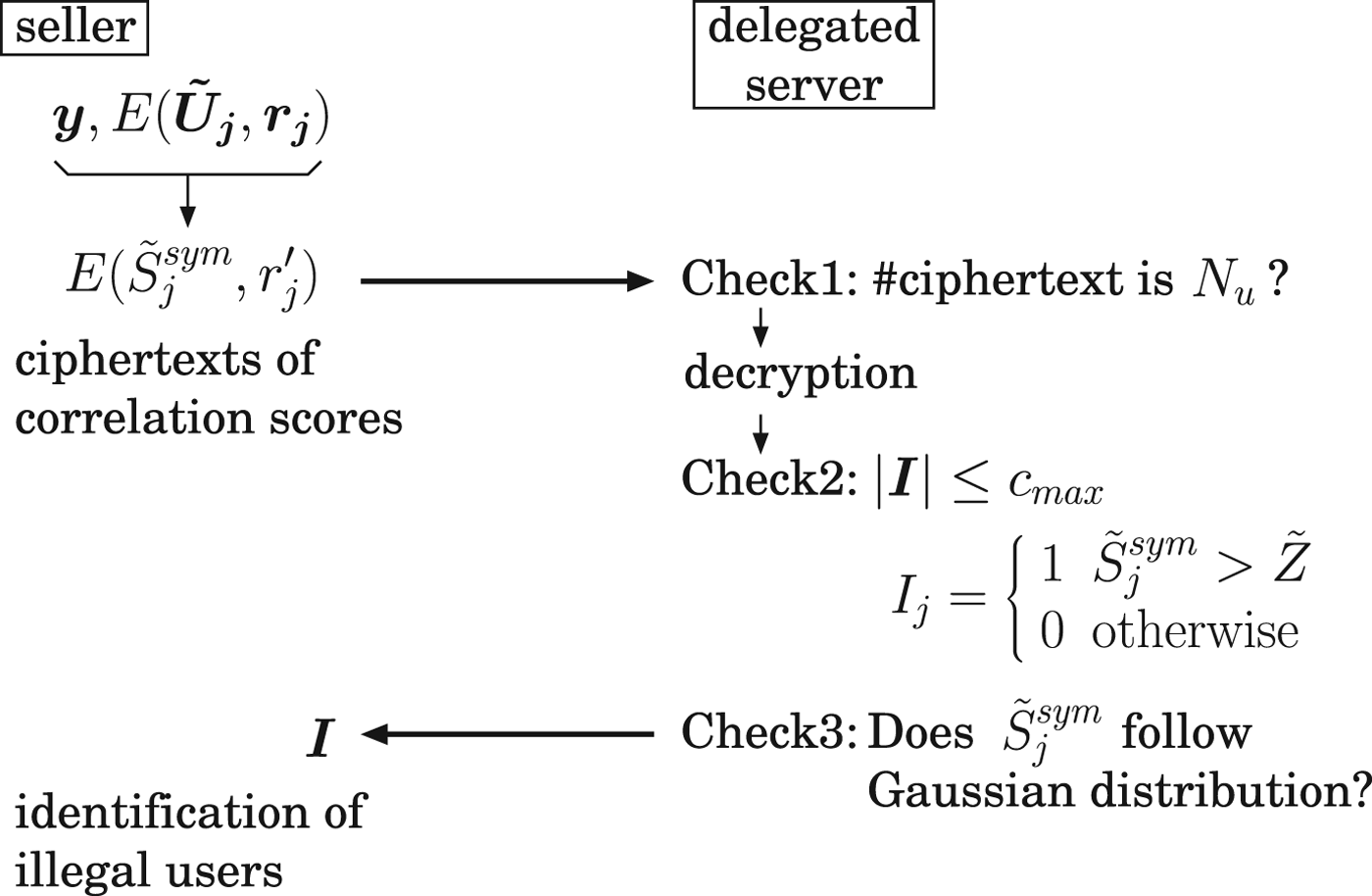
Fig. 2. Illustration of tracing protocol.
After the protocol, the seller can claim the illegal action of identified users to a judge by showing the items used in the protocol.
If an anonymous fingerprinting protocol is employed, it is necessary to check the pseudonyms at the center for the identification.
IV. SECURITY ANALYSIS
We assume that a trusted center initializes the parameters of fingerprinting code ℓ, c max, ![]() $\vec {\bi p}_i=(p_1,\, \ldots ,\, p_\ell )$, U j,i, and assigns codewords
$\vec {\bi p}_i=(p_1,\, \ldots ,\, p_\ell )$, U j,i, and assigns codewords ![]() $\vec {\bi X}_j$ to users. These parameters must be kept secret from a seller.
$\vec {\bi X}_j$ to users. These parameters must be kept secret from a seller.
A) Between trusted center and seller
As shown in equation (7), the weighting parameters U j,i are dependent on the each element X j,i of codeword ![]() $\vec {\bi X}_j$ and the bias probability p i. If a seller gets the weighting parameters, these parameters can be analyzed by comparing i-th elements U j,i among N u users for 1 ≤ i ≤ ℓ. In the proposed method, the weighting parameters are encrypted so as to keep X j,i and p i secret.
$\vec {\bi X}_j$ and the bias probability p i. If a seller gets the weighting parameters, these parameters can be analyzed by comparing i-th elements U j,i among N u users for 1 ≤ i ≤ ℓ. In the proposed method, the weighting parameters are encrypted so as to keep X j,i and p i secret.
Because of the random number used at the encryption, two ciphertexts E(m, r 1) and E(m, r 2) are indistinguishable for any 0 ≤ m < N and r 1 ≠ r 2. Hence, among N u users, i-th weighting parameter U j,i has two candidates ![]() $-\sqrt {p_i/(1-p_i)}$ and
$-\sqrt {p_i/(1-p_i)}$ and ![]() $\sqrt {(1-p_i)/p_i}$ as shown in equation (7), a seller cannot distinguish them from the observation of their ciphertexts
$\sqrt {(1-p_i)/p_i}$ as shown in equation (7), a seller cannot distinguish them from the observation of their ciphertexts ![]() $E(\vec {\bi U}_j,\, \vec {\bi r}_j)$, (1 ≤ j ≤ N u). It means that no information about the elements of codewords
$E(\vec {\bi U}_j,\, \vec {\bi r}_j)$, (1 ≤ j ≤ N u). It means that no information about the elements of codewords ![]() $\vec {\bi X}_j$ as well as
$\vec {\bi X}_j$ as well as ![]() $\vec {\bi p}$ from the ciphertexts. Therefore, the seller gets no information about users from the ciphertexts transmitted from a trusted center.
$\vec {\bi p}$ from the ciphertexts. Therefore, the seller gets no information about users from the ciphertexts transmitted from a trusted center.
B) Between seller and delegated server
When a malicious seller makes a request with dummy ciphertexts, a delegated server can reject the request in the following reasons.
If the number of ciphertexts is not N u, the request is immediately judged invalid. Hence, a seller must send N u ciphertexts that must be the ciphertexts of correlation scores. In case of dummy ciphertexts, the server will be able to find an illegal action of seller by checking the decrypted values. It is sufficient for the server to analyze the statistical distribution of the scores whether it follows Gaussian. In addition, when the number of values exceeding the threshold ![]() $\tilde {Z}$ is more than c max, the ciphertexts are regarded as guilty.
$\tilde {Z}$ is more than c max, the ciphertexts are regarded as guilty.
If a malicious seller makes a dummy ciphertext ![]() $E(\tilde {U}_{j,i})^\gamma $ by using a certain large integer γ. Then, the decrypted value becomes
$E(\tilde {U}_{j,i})^\gamma $ by using a certain large integer γ. Then, the decrypted value becomes ![]() $\gamma \tilde {U}_{j,i} > \tilde {Z}$ with a probability
$\gamma \tilde {U}_{j,i} > \tilde {Z}$ with a probability ![]() $\Pr [X_{j,i}=1]=p_i$. Since a seller does not know the parameters p i,
$\Pr [X_{j,i}=1]=p_i$. Since a seller does not know the parameters p i, ![]() $\tilde {U}_{j,i}$, and
$\tilde {U}_{j,i}$, and ![]() $\tilde {Z}$, it is difficult to control the number of values exceeding the threshold
$\tilde {Z}$, it is difficult to control the number of values exceeding the threshold ![]() $\tilde {Z}$. If the seller can make a request many times, the control might be possible. However, the number of request is limited in the proposed method, and hence, it is difficult.
$\tilde {Z}$. If the seller can make a request many times, the control might be possible. However, the number of request is limited in the proposed method, and hence, it is difficult.
V. EXPERIMENTAL RESULTS
A) Accuracy
In the proposed method, we use a scaling parameter α to ensure the precision of weighting parameters U j,i. The degradation of traceability is measured under the following conditions. We use a Nuida code [Reference Nuida4] with c max = 8 and ℓ = 1024. The number of users is N u = 10 000 and the threshold is calculated by the rare event simulator [Reference Cérou, Furon and Guyader7] with a false-positive probability set to be 10−8. The tracing protocol is run for 1000 times, and the average number of colluders detected from a pirated copy are calculated in the simulation. Table 2 shows the number of detected colluders for some typical collusion strategies when the number of colluders is 4, where “original” is the case that no rounding operation is performed to U j,i. By changing the number of colluders, the traceability is measured for the majority voting strategy, which result is shown in Fig. 3. As the results in case of α ≤ 1000 are very close to the results of the original, their results are omitted in the figure. Because of the probabilistic setting of threshold ![]() $\tilde {Z}$ by the rare event simulator, the values in the tables are slightly fluctuated, especially in case of α = 10 in Table 2. Nevertheless, it can be said from these results that α ≥ 1000 is sufficient to assure the traceability.
$\tilde {Z}$ by the rare event simulator, the values in the tables are slightly fluctuated, especially in case of α = 10 in Table 2. Nevertheless, it can be said from these results that α ≥ 1000 is sufficient to assure the traceability.
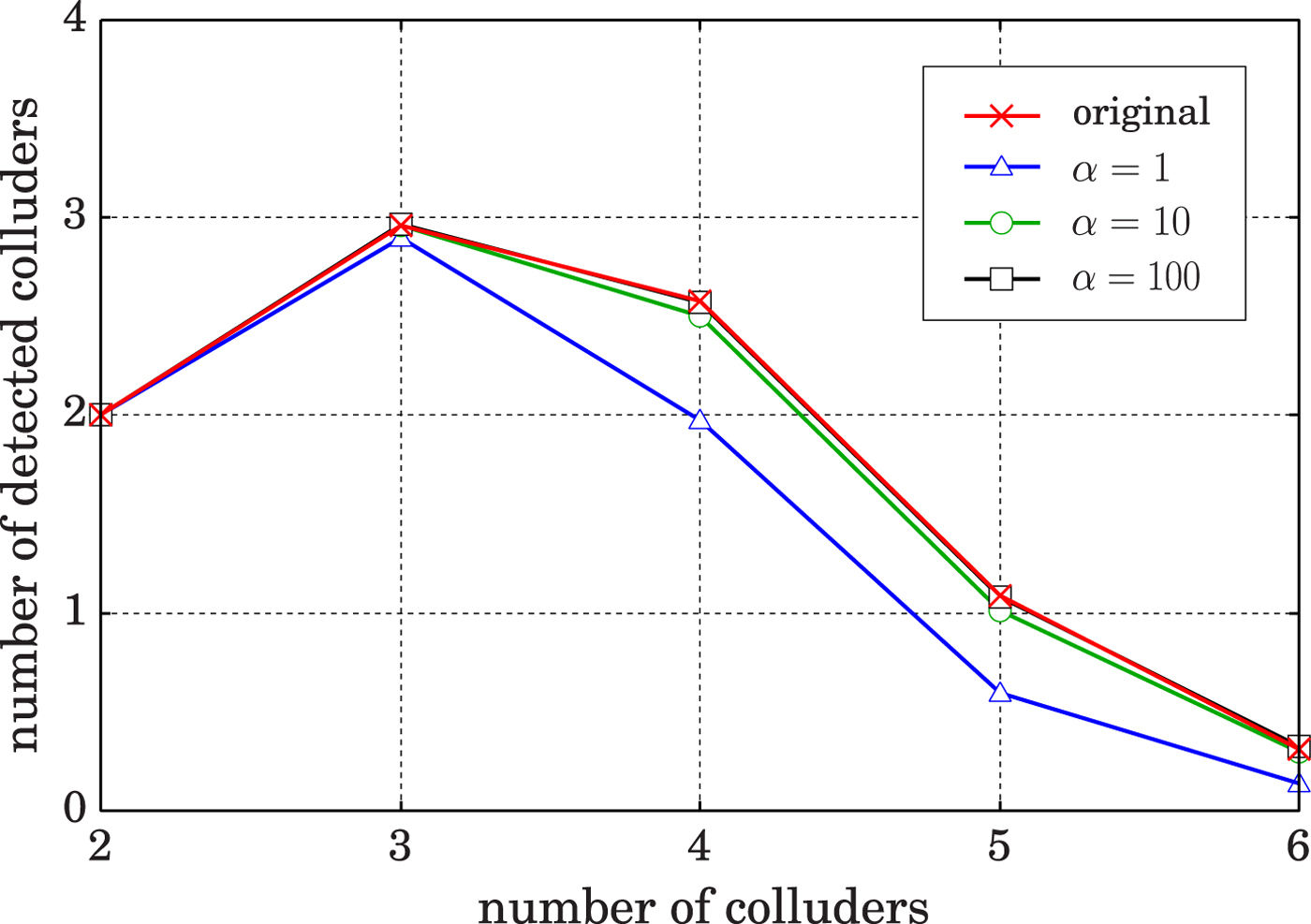
Fig. 3. Comparison of traceability against majority voting strategy.
Table 2. Number of detected colluders when four colluders produce a pirated copy.

B) Computational costs
At the tracing protocol, a seller calculates a correlation score in an encrypted domain by executing the modular multiplication (MM) and modular exponentiation (ME). The number of MM and ME is ℓ times for each score. Hence, the computational cost is linearly increased with the number of users N u.
We implemented the protocol and measured the time consumption under the following computer environment. The CPU is AMD Ryzen 7 2700X and the RAM memory is 32 GBytes. We use the GNU C compiler and GNU multiple precision (GMP) library at a X86-64 CentOS 7.5 linux. Table 3 shows the amount of time consumption both at the seller and delegated server.
Table 3. Time consumption [sec.] when majority voting is performed.

The computational costs for calculating correlation scores in an encrypted domain is10 times larger than the costs for decryption. If y i = 1, no operation is performed at the calculation of ![]() $E(\tilde {U}_{j,i},\, r_{j,i})^{2y_i-1}$ in equation (11). Otherwise, the multiplicative inverse
$E(\tilde {U}_{j,i},\, r_{j,i})^{2y_i-1}$ in equation (11). Otherwise, the multiplicative inverse ![]() $E(\tilde {U}_{j,i},\, r_{j,i})^{-1}$ is calculated. The computational cost for such an operation is much less than the costs for the ME at the decryption.
$E(\tilde {U}_{j,i},\, r_{j,i})^{-1}$ is calculated. The computational cost for such an operation is much less than the costs for the ME at the decryption.
It is noted that the time consumption is dependent on the number of users N u and the code length ℓ, which is O(N uℓ). At the setup of fingerprinting system, N u and c max must be assumed to derive its corresponding ℓ as well as the time consumption.
Although the computational costs are increased in total in the proposed system, our main objective is to reduce the burden at a trusted center. If the center manages several systems, it is desirable to reduce the burden as small as possible. Once the center setups the environment of fingerprinting system, no further work is required, which is the main advantage. Therefore, a seller is responsible for the identification of colluders when a pirated copy is found. In this sense, a delegated server supports the seller to reduce the computational burden without getting useful information about innocent users as well as colluders.
C) Communication costs
When a ciphertext size is 4096 bits and the length of codeword is ℓ = 1024, the bit-length of ![]() $E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ is 0.5 MBytes (=4 194 304 bits). As mentioned in Section 3.2, the total size is linearly increased with the number of users N u. In case of N u = 1000, the amount of data transmitted from a trusted center to a seller is 500 MBytes.
$E(\vec {\bi U}_j,\, \vec {\bi r}_j)$ is 0.5 MBytes (=4 194 304 bits). As mentioned in Section 3.2, the total size is linearly increased with the number of users N u. In case of N u = 1000, the amount of data transmitted from a trusted center to a seller is 500 MBytes.
The size of all codewords is N uℓ bits because each element X j,i is binary. Because of the encryption, the size becomes 4096 times bigger than the original one. In order to suppress the increase, an alternative method is to assign an index. A trusted center generates 2n ciphertexts for i-th weight; ![]() $n_{p_i,0}$ ciphertexts
$n_{p_i,0}$ ciphertexts ![]() $E(-\sqrt {p_i/(1-p_i)},\, r_{t, i})$,
$E(-\sqrt {p_i/(1-p_i)},\, r_{t, i})$, ![]() $(1\le t\le n_{p_i,0})$ and
$(1\le t\le n_{p_i,0})$ and ![]() $n_{p_i,1}$ ciphertexts
$n_{p_i,1}$ ciphertexts ![]() $E(\sqrt {(1-p_i)/p_i},\, r_{t, i})$,
$E(\sqrt {(1-p_i)/p_i},\, r_{t, i})$, ![]() $(1\le t\le n_{p_i,1})$, where
$(1\le t\le n_{p_i,1})$, where ![]() $2^n=n_{p_i,0}+n_{p_i,1}$ and
$2^n=n_{p_i,0}+n_{p_i,1}$ and ![]() $n_{p_i,1}= {\rm round}(2^np_i)$. Then, the total number of ciphertexts is 2nℓ, whose size is 2n−1 MBytes. In addition to these ciphertexts, the center generates a list of obfuscated codewords
$n_{p_i,1}= {\rm round}(2^np_i)$. Then, the total number of ciphertexts is 2nℓ, whose size is 2n−1 MBytes. In addition to these ciphertexts, the center generates a list of obfuscated codewords
VI. TOWARD OPTIMAL SCORING FUNCTION
The above scoring function is said to be non-informed because it is independent with the collusion strategy and the number of colluders. If such information is available at the detector side, an optimal scoring function can be employed to discriminate colluders' score from innocents' as much as possible [Reference Furon and Preire26]. Because of the difficulty in the realization of optimal scoring function, the scoring function has been adjusted for a certain fixed collusion strategy to achieve better performance than equation (8) [Reference Meerwald and Furon27–Reference Laarhoven30].
In binary fingerprinting codes, the number of symbols “0” and “1” is generally balanced because of the design of the codeword. After a collusion attack, the number of symbols is not always balanced in a pirated codeword. Such a bias of symbols is utilized to calculate weights for correlation scores in [Reference Kuribayashi and Funabiki31], whose traceability is close to the optimal scoring function.
For the improvement of the performance of Tardos code, Nuida et al. [Reference Nuida4] presented a discrete version of the bias distribution, which is customized for a given c max. Because of its discrete bias distribution in Nuida code, it is possible to classify each symbol of a codeword into some groups corresponding to the bias probabilities p i. Let n c be the number of candidates of p i. Then, the ℓ symbols X j,i of codeword can be divided into n c groups of length ℓξ, where ![]() $\sum\nolimits_{\xi = 1} {n_c} \ell _\xi = \ell $. The numbers of symbols “1” and “0” are denoted by ℓξ,1 and ℓξ,0, which satisfy
$\sum\nolimits_{\xi = 1} {n_c} \ell _\xi = \ell $. The numbers of symbols “1” and “0” are denoted by ℓξ,1 and ℓξ,0, which satisfy ![]() $\ell _{\xi ,1}+\ell _{\xi ,0}=\ell _\xi $. Then, the correlation score
$\ell _{\xi ,1}+\ell _{\xi ,0}=\ell _\xi $. Then, the correlation score ![]() $S^{Bias}_{j,i,\xi }$ at ξ-th group is represented by
$S^{Bias}_{j,i,\xi }$ at ξ-th group is represented by
 $$S_{j,i,\xi }^{Bias} = \left\{ {\matrix{ {\displaystyle{{\ell _{\xi ,1}} \over {\ell _\xi }}S_{j,i}^{sym} } \hfill & {{\rm if}\; y_i = 0} \hfill \cr {\displaystyle{{\ell _{\xi ,0}} \over {\ell _\xi }}S_{j,i}^{sym} } \hfill & {{\rm if}\; y_i = 1} \hfill \cr } } \right.,$$
$$S_{j,i,\xi }^{Bias} = \left\{ {\matrix{ {\displaystyle{{\ell _{\xi ,1}} \over {\ell _\xi }}S_{j,i}^{sym} } \hfill & {{\rm if}\; y_i = 0} \hfill \cr {\displaystyle{{\ell _{\xi ,0}} \over {\ell _\xi }}S_{j,i}^{sym} } \hfill & {{\rm if}\; y_i = 1} \hfill \cr } } \right.,$$and the total score is ![]() $S_j^{Bias} = \sum\nolimits_i {\sum\nolimits_\xi {S_{j,i,\xi }^{Bias} } } $. In [Reference Kuribayashi and Funabiki31], a collusion strategy is estimated into three types, and the above score
$S_j^{Bias} = \sum\nolimits_i {\sum\nolimits_\xi {S_{j,i,\xi }^{Bias} } } $. In [Reference Kuribayashi and Funabiki31], a collusion strategy is estimated into three types, and the above score ![]() $S^{Bias}_j$ is further modified according to the estimated type. For simplicity of explanation, we omit the detailed description in this paper (see for detail in [Reference Kuribayashi and Funabiki31]). Since the number of symbols “1” and “0” can be measured from a direct observation of pirated codeword, it is not difficult to employ the score
$S^{Bias}_j$ is further modified according to the estimated type. For simplicity of explanation, we omit the detailed description in this paper (see for detail in [Reference Kuribayashi and Funabiki31]). Since the number of symbols “1” and “0” can be measured from a direct observation of pirated codeword, it is not difficult to employ the score ![]() $S^{Bias}_j$.
$S^{Bias}_j$.
VII. CONCLUSION
In this paper, we presented a decentralized tracing protocol by delegating authority to a delegated server from a trusted center. Under the assumption that the server does not collude with a seller, information about fingerprinting code can be kept secret from the seller. Due to the decentralization, a trusted center only works at the initialization phase. When a pirated copy is found, the seller tries to calculate correlation scores in an encrypted domain and requests the decentralized server to classify the guilty users by deciphering the ciphertexts of correlation scores. One of our future works is to reduce the communication costs between the trusted center and seller.
FINANCIAL SUPPORT
This research was partially supported by JSPS KAKENHI Grant Number JP16K00185.
Minoru Kuribayashi received B.E., M.E., and D.E degrees from Kobe University, Japan, in 1999, 2001, and 2004. From 2002 to 2007, he was a Research Associate in the Department of Electrical and Electronic Engineering, Kobe University. In 2007, he was appointed as an Assistant Professor at the Division of Electrical and Electronic Engineering, Kobe University. Since 2015, he has been an Associate Professor in the Graduate School of Natural Science and Technology, Okayama University. His research interests include digital watermarking, information security, cryptography, and coding theory. He received the Young Professionals Award from IEEE Kansai Section in 2014.
Nobuo Funabiki received the B.S. and Ph.D. degrees in Mathematical Engineering andInformation Physics from the University of Tokyo, Japan, in 1984 and 1993, respectively. He received the M.S. degree in Electrical Engineering from Case Western Reserve University, USA, in 1991. From 1984 to 1994, he was with the System Engineering Division, Sumitomo Metal Industries, Ltd., Japan. In 1994, he joined the Department of Information and Computer Sciences at Osaka University, Japan, as as Assistant Professor, and became an Associate Professor in 1995. He stayed at the University of Illinois, Urbana-Champaign, in 1998, and at the University of California, Santa Barbara, in 2000–2001, as a Visiting Researcher. In 2001, he moved to the Department of Communication Network Engineering (currently, Electrical and Communication Engineering) at Okayama University as a Professor. His research interests include computer network, optimization algorithm, image processing, educational technology, Web technology, and network security.








