We consider the boundary-value problems corresponding to the scattering of a time-harmonic acoustic plane wave by a multi-layered obstacle with a sound-soft, hard or penetrable core. Firstly, we construct in closed forms the normalized scattering amplitudes and prove the classical reciprocity and scattering theorems for these problems. These results are then used to study the spectrum of the scattering amplitude operator. The scattering cross-section is expressed in terms of the forward value of the corresponding normalized scattering amplitude. Finally, we develop a more general theory for scattering relations.

In this paper the scattered progressive waves are determined due to progressive waves incident normally on certain types of partially immersed and completely submerged vertical porous barriers in water of infinite depth. The forms are approximate only, and are obtained using perturbation theory for nearly hard or soft barriers having high and low porosities respectively. The results for arbitrary porosity are difficult to obtain, in contrast to the well known hard limit of impermeable barriers.

In this paper we propose a systematic theoretical procedure for the constructive approximation of non-linear operators and show how this procedure can be applied to the modelling of dynamical systems. We extend previous work to show that the model is stable to small disturbances in the input signal and we pay special attention to the role of real number parameters in the modelling process. The implications of computability are also discussed. A number of specific examples are presented for the particular purpose of illustrating the theoretical procedure.

A new derivation of the averaged heat and mass transport equations for two-phase flows is presented. A volume averaging technique is used in which averaging is perform over both phases simultaneously in order to derive equations that describe transport the mixture, rather than transport in each phase. The derivation is particularly applicable to incompressible liquid/solid systems in which the two phases are tightly coupled. An example of the numerical solution of the equations is then presented in which a thermally convecting suspension is modelled. It is seen that large-scale instability can result from the interaction of thermal and compositional density gradients.

A model for bushfire spread is proposed, in which radiative heat transfer, species consumption and flammable gas production are taken into account. It is shown that fire propagation in this model does not occur as a one-dimensional travelling wave, except for smouldering combustion of wet bushland. Numerical solutions for the evolution of a line fire are obtained using a diagonally implicit finite difference scheme, and the effects of firebreaks and uncleared combustible debris are studied. An energy theorem is presented for the case of a spreading two-dimensional fire, and numerical results are illustrated.

In this paper, optimal consumption and investment decisions are studied for an investor who has available a bank account and a stock whose price is a log normal diffusion. The bank pays at an interest rate r(t) for any deposit, and vice takes at a larger rate r′(t) for any loan. Optimal strategies are obtained via Hamilton-Jacobi-Bellman (HJB) equation which is derived from dynamic programming principle. For the specific HARA case, we get the optimal consumption and optimal investment explicitly, which coincides with the classical one under the condition r′(t) ≡ r(t)

In the paper King [8], a new class of source solutions was derived for the nonlinear diffusion equation for diffusivities of the form D(c) = D0cm/(l - vc)m+2. Here we extend this method for the nonlinear diffusion and convection equation

to obtain mass-conserving source solutions for a nonlinear conductivity function K(c) = K0cm+2/(l - vc)m+1. In particular we consider the cases m = -1,0, and 1, where fully analytical solutions are available. Furthermore we provide source solutions for the exponential forms of the diffusivity and conductivity as given by D(c) = D0c−2e−n/c and K(c) = K0ce−n/c.

In the present paper the problem of reflection of water waves by a nearly vertical porous wall in the presence of surface tension has been investigated. A perturbational approach for the first-order correction has been employed as compared with the corresponding vertical wall problem. A mixed Fourier transform together with the regularity property of the transformed function along the positive real axis has been used to obtain the potential functions along with the reflection coefficients up to first order. Whilst the problem of water of infinite depth is the subject matter of the present paper, a similar approach is applicable to problems associated with water of finite depth.

We will study one-parameter families 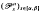of differentiable optimal control problems given by:

Here, at given times t the inequality constraint functions are of semi-infinite nature, the objective functional may also be of max-type. For each s ∈ ℝ the problem 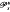is equivalent to a one-parameter family (Ps (t))t∈[a,b] of differentiable optimization problems. From these the consideration of generalized critical trajectories, such as a local minimum trajectory, comes into our investigation. According to a concept introduced by Hettich, Jongen and Stein in optimization, we distinguish eight types of generalized critical trajectories. Under suitable continuity, compactness and integrability assumptions, those problems, which exclusively have generalized critical points being of one of these eight types, are generic. We study normal forms and characteristic examples, locally around these trajectories.

Moreover, we indicate the related concept of structural stability of optimal control problems 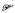due to the topological behaviour of the lower level sets under small data perturbations. Finally, we discuss the numerical consequences of our investigations for pathfollowing techniques with jumps.

A train of surface water waves normally incident on a thin vertical wall completely submerged in deep water and having a gap, experiences reflection by the wall and transmission through the gaps above and in the wall. Using Havelock's expansion of water wave potential, two different integral equation formulations of the problem are presented. While the first formulation involves multiple integral equations which are solved here by reducing them to a singular integral equation with Cauchy kernel in a double interval, the second formulation involves a first-kind singular integral equation in a double interval with a combination of logarithmic and Cauchy kernel, the solution of which is obtained by utilizing the solution of a singular integral equation with Cauchy kernel in (0, ∞) and also in a double interval. The reflection coefficient is evaluated by both the methods.

This paper contains a detailed formulation of advanced tumor therapy with neutron beams as a mixed boundary initial value problem for multigroup neutron diffusion in a composite 3D multiregional system. By applying a vector-matrix composite region finite-integral transformation we derive the principal operational solution to this problem as the group-regional neutron flux distribution inside the tumor 3D subregions. The principal solution is then converted into expressions of various order approximation, which may be directly programmed on a computer.

How to obtain a workable initial guess to start an optimal control (control parametrization) algorithm is an important question. In particular, for a system of multi-link vertical planar robot arms moving under the effect of gravity and applied torques (which can exhibit chaotic behaviour), a non-workable initial guess of torques may cause integration failure regardless of what numerical packages are used. In this paper, we address this problem by introducing a simple and intuitive “Blind Man” algorithm. Theoretical justification as well as a numerical example is provided.

A chemical reactor problem is considered governed by partial differential equations. We wish to control the input temperature and the input oxygen concentration so that the actual output temperature can be as close to the desired output temperature as possible. By linearizing the differential equations around a nominal equation and then applying a finite-element Galerkin Scheme to the resulting system, the original problem can be converted into a sequence of linearly-constrained quadratic programming problems.

The linear stability properties are examined of long wavelength vortex modes in two time-periodic flows. These flows are the motion which is induced by a torsionally oscillating cylinder within a viscous fluid and, second, the flow which results from the sinusoidal heating of an infinite layer of fluid. Previous studies concerning these particular configurations have shown that they are susceptible to vortex motions and linear neutral curves have been computed for wavenumbers near their critical value. These computations become increasingly difficult for long wavelength motions and here we consider such modes using asymptotic methods. These yield simple results which are formally valid for small wavenumbers and we show that the agreement between these asymptotes and numerical solutions is good for surprisingly large wavenumbers. The two problems studied share a number of common features but also have important differences and, between them, our methods and results provide a basis which can be extended for use with other time-periodic flows.

Two coupled nonlinear evolution equations correct to fourth order in wave steepness are derived for a three-dimensional wave packet in the presence of a thin thermocline. These two coupled equations are reduced to a single equation on the assumption that the space variation of the amplitudes takes place along a line making an arbitrary fixed angle with the direction of propagation of the wave. This single equation is used to study the stability of a uniform wave train. Expressions for maximum growth rate of instability and wave number at marginal stability are obtained. Some of the results are shown graphically. It is found that a thin thermocline has a stabilizing influence and the maximum growth rate of instability decreases with the increase of thermocline depth.

The motion of a two-dimensional bubble rising at a constant velocity U in an inclined tube of width H is considered. The bubble extends downwards without limit, and is bounded on the right by a wall of the tube, and on the left by a free surface. The same flow configuration describes also a jet emerging from a nozzle and falling down along an inclined wall. The acceleration of gravity g and the surface tension T are included in the free surface condition. The problem is characterized by the Froude number the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained via series truncation for all values of 0 < β < π. The results extend previous calculations of Vanden-Broeck [12–14] for β = π/2 and of Couët and Strumolo [3] for 0 < β < π/2. It is found that the behavior of the solutions depends on whether 0 < β 2π/3 or 2π/3 ≤ β < π. When T = 0, it is shown that there is a critical value F of Froude number for each 0 < β 2π/3 such that solutions with γ = 0, π/3 and π - β occur for F > Fc F = Fc and F < Fc respectively, and that all solutions are characterized by γ = 0 for 2π/3 ≤ β < π. When a small amount of surface tension T is included in the free surface condition, it is found that for each 0 < β < π there exists an infinite discrete set of values of F for which γ = π - β. A particular value F* of the Froude number for which T = 0 and γ = π - β is selected by taking the limit as T approaches zero. The numerical values of F* and the corresponding free surface profiles are found to be in good agreement with experimental data for bubbles rising in an inclined tube when 0 < β < π/2.

In this paper we study parametric optimal control problems governed by a nonlinear parabolic equation in divergence form. The parameter appears in all the data of the problem, including the partial differential operator. Using as tools the G-convergence of operators and the Γ-convergence of functionals, we show that the set-valued map of optimal pairs is upper semicontinuous with respect to the parameter and the optimal value function responds continuously to changes of the parameter. Finally in the case of semilinear systems we show that our framework can also incorporate systems with weakly convergent coefficients.

The generalized diffusion equation with a nonlinear source term which encompasses the Fisher, Newell-Whitehead and Fitzhugh-Nagumo equations as particular forms and appears in a wide variety of physical and engineering applications has been analysed for its generalized symmetries (isovectors) via the isovector approach. This yields a new and exact solution to the generalized diffusion equation. Further applications of group theoretic techniques on the travelling wave reductions of the Fisher, Newell-Whitehead and Fitzhugh-Nagumo equations result in integrability conditions and Lie vector fields for these equations. The Lie group of transformations obtained from the exponential vector fields reduces these equations in generalized form to a standard second-order differential equation of nonlinear type, which for particular cases become the Weierstrass and Jacobi elliptic equations. A particular solution to the generalized case yields the exact solutions that have been obtained through different techniques. The group-theoretic integrability relations of the Fisher and Newell-Whitehead equations have been cross-checked through Painlevé analysis, which yields a new solution to the Fisher equation in a complex-valued function form.

An integral inequality is established involving a probability density function on the real line and its first two derivatives. This generalizes an earlier result of Sato and Watari. If f denotes the probability density function concerned, the inequality we prove is that

under the conditions β > α 1 and 1/(β+1) < γ ≤ 1.

We study differential game problems in which the players can select different maximal monotone operators for the governing evolution system. Setting up our problem on a real Hilbert space, we show that the Elliott-Kalton upper and lower value of the game are viscosity solution of some Hamilton-Jacobi-Isaacs equations. Uniqueness is obtained by assuming condition analogous to the classical Isaacs condition, and thus the existence of value of the game follows.