We shall study continuous-time Markov chains on the nonnegative integers which are both irreducible and transient, and which exhibit discernible stationarity before drift to infinity “sets in”. We will show how this ‘quasi’ stationary behaviour can be modelled using a limiting conditional distribution: specifically, the limiting state probabilities conditional on not having left 0 for the last time. By way of a dual chain, obtained by killing the original process on last exit from 0, we invoke the theory of quasistationarity for absorbing Markov chains. We prove that the conditioned state probabilities of the original chain are equal to the state probabilities of its dual conditioned on non-absorption, thus allowing to establish the simultaneous existence and then equivalence, of their limiting conditional distributions. Although a limiting conditional distribution for the dual chain is always quasistationary distribution in the usual sense, a similar statement is not possible for the original chain.

A local existence and uniqueness result is proved for the three-dimensional Euler-Poisson system without a pressure term which arises in plasma physics.

This paper studies a system proposed by K. Gopalsamy and P. X. Weng to model a population growth with feedback control and time delays. Sufficient conditions are established under which the positive equilibrium of the system is globally attracting. The conjecture proposed by Gopalsamy and Weng is here confirmed and improved.

A steady two-dimensional free-surface flow in a channel of finite depth is considered. The channel ends abruptly with a barrier in the form of a vertical wall of finite height. Hence the stream, which is uniform far upstream, is forced to go upward and then falls under the effect of gravity. A configuration is examined where the rising stream splits into two jets, one falling backward and the other forward over the wall, in a fountain-like manner. The backward-going jet is assumed to be removed without disturbing the incident stream. This problem is solved numerically by an integral-equation method. Solutions are obtained for various values of a parameter measuring the fraction of the total incoming flux that goes into the forward jet. The limit where this fraction is one is also examined, the water then all passing over the wall, with a 120° corner stagnation point on the upper free surface.

By applying Laplace transform theory to solve first-order homogeneous differential-difference equations it is conjectured that a resulting infinite sum of a series may be expressed in closed form. The technique used in obtaining a series in closed form is then applied to other examples in teletraffic theory and renewal processes.

A general framework is developed for constructing higher order spectral refinement schemes for a simple eigenvalue. Well-known techniques for ordinary spectral refinement are carried over to higher order spectral refinement yielding faster rates of convergence. Numerical examples are given by considering an integral operator.

A three stage procedure for the analysis and least-cost design of looped water distribution networks is considered in this paper. The first stage detects spanning trees and identifies the true global optimum for the system. The second stage determines hydraulically feasible pipe flows for the network by the numerical solution of a set of non-linear simultaneous equations and shows that these solutions are contained within closed convex polygonal regions in the solution space bounded by singularities resulting from zero flows in individual pipes. Ideal pipe diameters, consistent with the pipe flows and the constant velocity constraint adopted to prevent the system degenerating into a branched network, are selected and costed. It is found that the most favourable optimum is in the vicinity of a vertex in the solution space corresponding to the minimum spanning tree. In the third stage, commercial pipes are specified and the design finalised. Upper bound formulae for the number of spanning trees and hydraulically feasible solutions in a network have also been proposed. The treatment of large networks by a heuristic procedure is described which is shown to result in significant economies compared with designs obtained by non-linear programming.

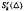Let Δ denote a triangulation of a planar polygon Ω. For any positive integer 0 ≤ r < k, let denote the vector space of functions in 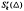Cr whose restrictions to each triangle of Δ are polynomials of total degree at most k. Such spaces, called bivariate spline spaces, have many applications in surface fitting, scattered data interpolation, function approximation and numerical solutions of partial differential equations. An important problem is to give the function expression. In this paper, we prove that, if (Δ, Ω) is type-X, then any bivariate spline function in can be expressed by a series of univariate polynomials and a special bivariate finite element function in 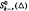satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space 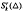. In addition, the dimension of 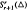for a kind of triangulation has been determined.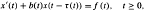

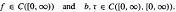
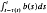In this paper, we consider the system governed via the coefficients of a semilinear elliptic equation and give the necessary conditions for optimal control. Furthermore, we obtain the necessary conditions for an optimal domain in a domain optimization problem.

Consider the forced differential equation with variable delay

where

We establish a sufficient condition for every solution to tend to zero. We also obtain a sharper condition for every solution to tend to zero when is asymptotically constant.