Research Article
The gliding motion of a bacterium: Flexibacter strain BH3
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 2-16
-
- Article
-
- You have access
- Export citation
Stiff systems of ordinary differential equations. Part 1. Completely stiff, homogeneous systems
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 17-51
-
- Article
-
- You have access
- Export citation
On representations of a generalized method of field quantization
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 52-63
-
- Article
-
- You have access
- Export citation
Exact solution of a difference approximation to Duffing's equation
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 64-77
-
- Article
-
- You have access
- Export citation
Equations for periodic solutions of a logistic difference equation
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 78-94
-
- Article
-
- You have access
- Export citation
The response to a hot spot in a combustion problem
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 95-102
-
- Article
-
- You have access
- Export citation
Effects of iron on a toroidal conductor
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 103-114
-
- Article
-
- You have access
- Export citation
Front Matter
ANZ volume 23 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 23 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

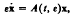
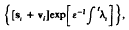
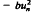 , where
, where 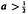 and
and 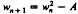 , where
, where 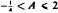 , although the equations obtained are valid for
, although the equations obtained are valid for