In this paper we consider a simple, nonlinear optimal control problem with sufficient convexity to enable us to formulate its dual problem. Both primal and dual problems will include constraints on both the states and controls. The constraints in one problem may cause the “optimal” dual states to be discontinuous. However, we will look at conditions under which the presence of constraints does not force discontinuities and the optimal states and costates are absolutely continuous.

The paper discusses solutions of period 4 for the difference equation

where k and m are real parameters, with k > 0. For given values of k and m there are at most three solutions with period 4 and equations are set up to determine the elements of these solutions and the stability of each solution. Only real solutions are considered. The procedure that is used to find these solutions allows unstable solutions to be identified as well as stable solutions.

In a previous paper, solutions of period 2 and period 3 were examined for this equation and there was evidence of anomalous behaviour in the way the stability intervals occurred. Some preliminary information about solutions of period 4 was mentioned in the discussion. The present paper provides more complete results, which confirm the anomalous behaviour and give a better idea of how the stability criterion changes for different families of solutions. These results are used to indicate the variety of behaviour that can be found for one-parameter systems by imposing suitable conditions on m and k.

Let L, T, S, and R be closed densely defined linear operators from a Hubert space X into X where L can be factored as L = TS + R. The equation Lu = f is equivalent to the linear system Tv + Ru = f and Su = v. If Lu = f is a two-point boundary value problem, numerical solution of the split system admits cruder approximations than the unsplit equations. This paper develops the theory of such splittings together with the theory of the Methods of Least Squares and of Collocation for the split system. Error estimates in both L2 and L∞ norms are obtained for both methods.

Strong system equivalence is defined for polynomial realizations of a rational matrix. It is shown that any polynomial realization is strongly system equivalent to a generalized state-space realization, and two generalized state-space realizations are strongly system equivalent if and only if they are constant system equivalent.

The notion of strong system equivalence, which was defined and studied in Anderson, Coppel and Cullen [1], is here given a module-theoretic characterization and a dynamical interpretation.

In this note, the weak duality theorem of symmetric duality in nonlinear programming and some related results are established under weaker (strongly Pseudo-convex/strongly Pseudo-concave) assumptions. These results were obtained by Bazaraa and Goode [1] under (stronger) convex/concave assumptions on the function.

Critical point behaviour of the diffusion length γ for the solutions of the radiative transfer equation deep in a homogenous medium is studied. The Legendre expansion of the medium's phase function P(cos ψ) is taken to be an infinite series and is characterized by the parameters h0, h1h2,…. A characteristic equation for γ is given in terms of an infinite continued fraction. 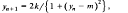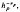From this equation it is shown that as any one of the hn, say hp, approaches zero, the others being held constant, γ behaves as , where the critical exponent is found to be vp = ½ for all p = 0, 1, 2,….