Research Article
An interior point method for linear programming
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 367-378
-
- Article
-
- You have access
- Export citation
Strong uniqueness in sequential linear programming
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 379-384
-
- Article
-
- You have access
- Export citation
Propagation of flame fronts
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 385-396
-
- Article
-
- You have access
- Export citation
Nonlinear interaction of positive and negative energy modes in Hamiltonian systems
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 397-424
-
- Article
-
- You have access
- Export citation
The isotropy mappings of Minkowski space-time generate the orthochronous poincaré group
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 425-433
-
- Article
-
- You have access
- Export citation
Functional differential equations determining steady size distributions for populations of cells growing exponentially
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 434-453
-
- Article
-
- You have access
- Export citation
An optimal strategy for the control of a train
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 454-471
-
- Article
-
- You have access
- Export citation
On hearing the shape of an arbitrary doubly-connected region in R2
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 472-483
-
- Article
-
- You have access
- Export citation
Duality for fractional minimax programming problems
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 484-492
-
- Article
-
- You have access
- Export citation
Index for Volume 31
Contents of Volume 31
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 493-494
-
- Article
-
- You have access
- Export citation
Front matter
ANZ volume 31 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 31 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

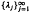 for the two-dimensional Laplacian using the asymptotic expansion of the spectral function
for the two-dimensional Laplacian using the asymptotic expansion of the spectral function 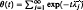 for small positive
for small positive