We consider a local projection stabilization based on biorthogonal systems for convection–diffusion–reaction differential equations with mixed boundary conditions. The approach based on biorthogonal systems is numerically more efficient than other existing approaches to obtain a uniform approximation for convection dominated problems. We prove optimal a priori error estimates for the proposed numerical technique. Numerical examples are presented to demonstrate the performance of the approach.

Recent higher-order explicit Runge–Kutta methods are compared with the classic fourth-order (RK4) method in long-term integration of both energy-conserving and lossy systems. By comparing quantity of function evaluations against accuracy for systems with and without known solutions, optimal methods are proposed. For a conservative system, we consider positional accuracy for Newtonian systems of two or three bodies and total angular momentum for a simplified Solar System model, over moderate astronomical timescales (tens of millions of years). For a nonconservative system, we investigate a relativistic two-body problem with gravitational wave emission. We find that methods of tenth and twelfth order consistently outperform lower-order methods for the systems considered here.

We consider the pricing of discretely sampled volatility swaps under a modified Heston model, whose risk-neutralized volatility process contains a stochastic long-run variance level. We derive an analytical forward characteristic function under this model, which has never been presented in the literature before. Based on this, we further obtain an analytical pricing formula for volatility swaps which can guarantee the computational accuracy and efficiency. We also demonstrate the significant impact of the introduced stochastic long-run variance level on volatility swap prices with synthetic as well as calibrated parameters.

When faced with the task of solving hyperbolic partial differential equations (PDEs), high order, strong stability-preserving (SSP) time integration methods are often needed to ensure preservation of the nonlinear strong stability properties of spatial discretizations. Among such methods, SSP second derivative time-stepping schemes have been recently introduced and used for evolving hyperbolic PDEs. In previous works, coupling of forward Euler and a second derivative formulation led to sufficient conditions for a second derivative general linear method (SGLM), which preserve the strong stability properties of spatial discretizations. However, for such methods, the types of spatial discretizations that can be used are limited. In this paper, we use a formulation based on forward Euler and Taylor series conditions to extend the SSP SGLM framework. We investigate the construction of SSP second derivative diagonally implicit multistage integration methods (SDIMSIMs) as a subclass of SGLMs with order 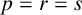$p=r=s$ and stage order 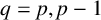$q=p,p-1$ up to order eight, where r is the number of external stages and s is the number of internal stages of the method. Proposed methods are examined on some one-dimensional linear and nonlinear systems to verify their theoretical order, and show potential of these schemes in preserving some nonlinear stability properties such as positivity and total variation.

We derive a nonlinear Schrödinger equation for the propagation of the three-dimensional broader bandwidth gravity-capillary waves including the effect of depth-uniform current. In this derivation, the restriction of narrow bandwidth constraint is extended, so that this equation will be more appropriate for application to a realistic sea wave spectrum. From this equation, an instability condition is obtained and then instability regions in the perturbed wavenumber space for a uniform wave train are drawn, which are in good agreement with the exact numerical results. As it turns out, the corrections to the stability properties that occur at the fourth-order term arise from an interaction between the mean flow and the frequency-dispersion term. Since the frequency-dispersion term, in the absence of depth-uniform current, for pure capillary waves is of opposite sign for pure gravity waves, so too are the corrections to the instability properties.