Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T11:13:02.920Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSMISSION OF ELASTIC WAVES IN ANISOTROPIC NEMATIC ELASTOMERS

Part of: Equilibrium statistical mechanics

Published online by Cambridge University Press:  02 July 2015

S. S. SINGH
S. S. SINGH*
Affiliation:
Department of Mathematics and Computer Science, Mizoram University, Aizawl 796 004, Mizoram, India email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of reflection and refraction of elastic waves due to an incident quasi-primary 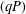$(qP)$ wave at a plane interface between two dissimilar nematic elastomer half-spaces has been investigated. The expressions for the phase velocities corresponding to primary and secondary waves are given. It is observed that these phase velocities depend on the angle of propagation of the elastic waves. The reflection and refraction coefficients corresponding to the reflected and refracted waves, respectively, are derived by using appropriate boundary conditions. The energy transmission of the reflected and refracted waves is obtained, and the energy ratios and the reflection and refraction coefficients are computed numerically.

Keywords

nematic elastomersqP-waveqSV-wavereflectionrefractionphase velocity

MSC classification

Primary: 82B24: Interface problems; diffusion-limited aggregation
Type
Research Article
Information
The ANZIAM Journal , Volume 56 , Issue 4 , April 2015 , pp. 381 - 396
Copyright
© 2015 Australian Mathematical Society 

References

Achenbach, J. D., Wave propagation in elastic solids (North-Holland, New York, 1978).Google Scholar
Alexe-Ionescu, A. L., Barberi, R., Barbero, G. and Giocondo, M., “Anchoring energy for nematic liquid crystals: contribution from the spatial variation of the elastic constants”, Phys. Rev. E 49 (1994) 5378–5388; doi:10.1103/PhysRevE.49.5378.CrossRefGoogle ScholarPubMed
Anderson, D. R., Carlson, D. E. and Fried, E., “A continuum-mechanical theory of nematic elastomers”, J. Elasticity 56 (1999) 33–58; doi:10.1023/A:1007647913363.CrossRefGoogle Scholar
Brand, H. R. and Pleiner, H., “Electrohydrodynamics of nematic liquid crystalline elastomers”, Physica A 208 (1994) 359–372; doi:10.1016/0378-4371(94)00060-3.CrossRefGoogle Scholar
Carcione, J. M., “Constitutive model and wave-equations for linear, viscoelastic, anisotropic media”, Geophysics 60 (1994) 537–548; doi:10.1190/1.1443791.CrossRefGoogle Scholar
Clarke, S. M., Tajbakhsh, A. R., Terentjev, E. M. and Warner, M., “Anomalous viscoelastic response of nematic elastomers”, Phys. Rev. Lett. 86 (2001) 4044–4047; doi:10.1103/PhysRevLett.86.4044.CrossRefGoogle ScholarPubMed
Conti, S., DeSimone, A. and Dolzmann, G., “Soft elastic response of stretched sheets of nematic elastomers: a numerical study”, J. Mech. Phys. Solids 50 (2002) 1431–1451; doi:10.1016/S0022-5096(01)00120-X.CrossRefGoogle Scholar
Deeg, F. W., Diercksen, K., Schwalb, G., Brauchle, C. and Reinecke, H., “Ultrasonic measurements of the anisotropic viscoelastic properties of nematic elastomers”, Phys. Rev. B 44 (1991) 2830–2833; doi:10.1103/PhysRevB.44.2830.CrossRefGoogle Scholar
de Gennes, P. G., Liquid crystals of one- and two-dimensional order (eds Helfrich, W. and Heppke, G.), (Springer, Berlin, 1980).Google Scholar
DeSimone, A. and Dolzmann, G., “Material instabilities in nematic elastomers”, Physica D 136 (2000) 175–191; doi:10.1016/S0167-2789(99)00153-0.CrossRefGoogle Scholar
DeSimone, A. and Teresi, T., “Elastic energies for nematic elastomers”, Eur. Phys. J. E 29 (2009) 191–204; doi:10.1140/epje/i2009-10467-9.CrossRefGoogle ScholarPubMed
Ericksen, J. L., “Anisotropic fluids”, Arch. Ration. Mech. Anal. 4 (1959) 231–237; doi:10.1007/BF00281389.CrossRefGoogle Scholar
Ericksen, J. L., “Conservation laws for liquid crystals”, Trans. Soc. Rheol. 5 (1961) 23–34; doi:10.1122/1.548883.CrossRefGoogle Scholar
Finkelmann, H., Greve, A. and Warner, M., “The elastic anisotropy of nematic elastomers”, Eur. Phys. J. E 5 (2001) 281–293; doi:10.1007/s101890170060.CrossRefGoogle Scholar
Finkelmann, H., Kundler, I., Terentjev, E. and Warner, M., “Critical stripe domain instability of nematic elastomers”, J. Phys. II 7 (1997) 1059–1069; doi:10.1051/jp2:1997171.Google Scholar
Fradkin, L. J., Kamotski, I. V., Terentjev, E. M. and Zakharov, D. D., “Low-frequency acoustic waves in nematic elastomers”, Proc. R. Soc. Lond. A 459 (2003) 2627–2642; doi:10.1098/rspa.2003.1153.CrossRefGoogle Scholar
Gebretsadkan, W. B. and Kalra, G. L., “Propagation of linear waves in relativistic anisotropic magnetohydrodynamics”, Phys. Rev. E 66 (2002) 057401–4; doi:10.1103/PhysRevE.66.057401.CrossRefGoogle ScholarPubMed
Greco, C. and Ferrarini, A., “Electroclinic effect in nematic liquid crystals: the role of molecular and environmental chirality”, Phys. Rev. E 87 (2013) 060501–4; doi:10.1103/PhysRevE.87.060501.CrossRefGoogle ScholarPubMed
Kupfer, J. and Finkelmann, H., “Nematic liquid single-crystal elastomers”, Makromol. Chem. Rapid Commun. 12 (1991) 717–726; doi:10.1002/marc.1991.030121211.CrossRefGoogle Scholar
Leslie, F. M., “Some constitutive equations for anisotropic fluids”, Quart. J. Mech. Appl. Math. 19(3) (1966) 357–370; doi:10.1093/qjmam/19.3.357.CrossRefGoogle Scholar
Leslie, F. M., “Some constitutive equations for liquid crystals”, Arch. Ration. Mech. Anal. 28 (1968) 265–283; doi:10.1007/BF00251810.CrossRefGoogle Scholar
Long, D. and Morse, D. C., “Linear viscoelasticity and director dynamics of nematic liquid crystalline polymer melts”, Europhys. Lett. 49 (2000) 255–261; doi:10.1209/epl/i2000-00142-5.CrossRefGoogle Scholar
Selinger, J. V., Jeon, H. G. and Ratna, B. R., “Isotropic–nematic transition in liquid-crystalline elastomers”, Phys. Rev. Lett. 89 (2002) 225701–4; doi:10.1103/PhysRevLett.89.225701.CrossRefGoogle ScholarPubMed
Selinger, J. V., Spector, M. S., Greanya, V. A., Weslowski, B. T., Shenoy, D. K. and Shashidhar, R., “Acoustic realignment of nematic liquid crystal”, Phys. Rev. E 66 (2002) 051708–7; doi10.1103/PhysRevE.66.051708.CrossRefGoogle Scholar
Singh, B., “Reflection of homogeneous elastic waves from free surface of nematic elastomer half-space”, J. Phys. D: Appl. Phys. 40 (2007) 584–592; doi:10.1088/0022-3727/40/2/038.CrossRefGoogle Scholar
Singh, S. S., “Effect of initial stresses on incident $\mathit{qSV}$-waves in pre-stressed elastic half-spaces”, ANZIAM J. 52 (2011) 359–371; doi:10.1017/S1446181111000757.CrossRefGoogle Scholar
Terentjev, E. M., Kamotski, I. V., Zakharov, D. D. and Fradkin, L. J., “Propagation of acoustic waves in nematic elastomers”, Phys. Rev. E 66 (2002) 052701; doi:10.1103/PhysRevE.66.052701.CrossRefGoogle ScholarPubMed