Article contents
Stiff systems of ordinary differential equations
II. Boundary-value problems for completely stiff systems
Published online by Cambridge University Press: 17 February 2009
Abstract
Solutions of the stiff system of linear differential equations
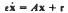
are obtained in a form yielding tight estimates of their properties, and conditions are obtained under which the operator norm of the map from r to the solution x does not become exponentially large for small values of ε. When these conditions are satisfied, the solutions are shown to be close to those of Ax + r = 0, save at any singular points of A, and in boundary layers. The behaviour of solutions near admissible singular points is also obtained.
The results are used to characterize those boundary-value problems for the above system in which the solution defines maps from the data that are of “moderate” operator norm. This leads to a constructive existence theory for a limited class of boundary-value problems for the nonlinear system
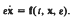
It is suggested that the treatment of more general classes of boundary-value problems may be simplified using these results. By the use of simple examples, the problems involving large operator norms are shown to be related to the stability properties of the possible branches of the outer solutions close to those of
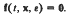
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1981
References
- 3
- Cited by


