Article contents
Stiff systems of ordinary differential equations. III. Partially stiff systems
Published online by Cambridge University Press: 17 February 2009
Abstract
The partially stiff system of ordinary differential equations
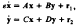
is studied by the methods developed in the earlier papers in this series. Here e is a small positive parameter, x and y are n- and m-vectors respectively, and A is nonsingular. A useful basis for the solution space of the homogeneous system is constructed and the method of variation of parameters is used to obtain useful representations of all solutions. Sufficient conditions are derived under which the formal approximation
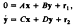
is close to the actual solution. it is found that purely imaginary eigenvalues for A require more stringent requirements for the formal technique to be valid. A brief discussion of the case when A is singular shows that there are a great number of possibilities requiring consideration for a general theory. it is suggested that local computation of such cases is likely to be the most effective weapon for any specific system.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1982
References
- 1
- Cited by


