Article contents
Spectral refinement using a new projection method
Published online by Cambridge University Press: 17 February 2009
Abstract
In this paper we consider two spectral refinement schemes, elementary and double iteration, for the approximation of eigenelements of a compact operator using a new approximating operator. We show that the new method performs better than the Galerkin, projection and Sloan methods. We obtain precise orders of convergence for the approximation of eigenelements of an integral operator with a smooth kernel using either the orthogonal projection onto a spline space or the interpolatory projection at Gauss points onto a discontinuous piecewise polynomial space. We show that in the double iteration scheme the error for the eigenvalue iterates using the new method is of the order of 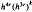 , where h is the mesh of the partition and k = 0, 1, 2,… denotes the step of the iteration. This order of convergence is to be compared with the orders
, where h is the mesh of the partition and k = 0, 1, 2,… denotes the step of the iteration. This order of convergence is to be compared with the orders 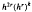 in the Galerkin and projection methods and
in the Galerkin and projection methods and 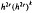 in the Sloan method. The error in eigenvector iterates is shown to be of the order of
in the Sloan method. The error in eigenvector iterates is shown to be of the order of 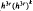 in the new method,
in the new method, 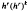 in the Galerkin and projection methods and
in the Galerkin and projection methods and 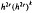 in the Sloan method. Similar improvement is observed in the case of the elementary iteration. We show that these orders of convergence are preserved in the corresponding discrete methods obtained by replacing the integration by a numerical quadrature formula. We illustrate this improvement in the order of convergence by numerical examples.
in the Sloan method. Similar improvement is observed in the case of the elementary iteration. We show that these orders of convergence are preserved in the corresponding discrete methods obtained by replacing the integration by a numerical quadrature formula. We illustrate this improvement in the order of convergence by numerical examples.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2004
References
- 6
- Cited by


