Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T04:04:03.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks on a quasi-steady-state approximation of the Navier-Stokes equation

Published online by Cambridge University Press:  17 February 2009

John R. Cannon  and
George H. Knightly
John R. Cannon
Affiliation:
Washington State University, Pullman, Washingtom 99164, U.S.A.
George H. Knightly
Affiliation:
University of Massachusetts, Amherst, Massachusetts 01003, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A quasi-steady-state apprcncimation to the Navier-Stokes equation is the corresponding equation with nonhomogeneous forcing term f(x, t), but with the term Vt deleted. For solutions that are zero on the boundary, the difference z between the solution of the Navier-Stokes equation and the solution of this quasi-steady-state approximation is estimated in the L2 norm ║z║ with respect to the spatial variables. For sufficiently large viscosity or sufficiently small body force f, the inequality

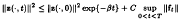
holds for 0 < t ≤ T and certain real numbres C, β > 0.

Type
Research Article
Information
The ANZIAM Journal , Volume 29 , Issue 4 , April 1988 , pp. 440 - 447
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Cannon, J. R., DiBenedetto, E. and Knightly, G. H., “The steady state Stefan problem with convection”, Arch. Rational Mech. Anal. 73 (1980), 79–97.CrossRefGoogle Scholar
[2]Cannon, J. R., DiBenedetto, E. and Knightly, G. H., “The bidimensional Stefan problem with convection: the time dependent case”, Comm. Partial Differential Equations 8 (1983), 1549–1604.CrossRefGoogle Scholar
[3]Joseph, D. D., Stability of Fluid Motions II (Springer-Verlag, New York, 1976).CrossRefGoogle Scholar
[4]Ladyzhenskaya, O. A., The Mathematical Theory of Viscous Incompressible Flow, 2nd Edition (Gordon and Breach, New York, 1969).Google Scholar
[5]Shinbrot, M., Lectures on Fluid Mechanics (Gordon and Breach, New York, 1973).Google Scholar
[6]Temam, R., Navier-Stokes Equations (North-Holland, New York, 1977).Google Scholar