Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T09:02:56.476Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME INEQUALITIES FOR THEORETICAL SPATIAL ECOLOGY

Part of: Special processes

Published online by Cambridge University Press:  10 October 2013

PAUL F. SLADE
PAUL F. SLADE*
Affiliation:
School of Mathematical Sciences, University of Adelaide, North Terrace, Adelaide, SA 5005, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Inequalities for spatial competition verify the pair approximation of statistical mechanics introduced to theoretical ecology by Matsuda, Satō and Iwasa, among others. Spatially continuous moment equations were introduced by Bolker and Pacala and use a similar assumption in derivation. In the present article, I prove upper bounds for the 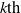$k\mathrm{th} $ central moment of occupied sites in the contact process of a single spatial dimension. This result shows why such moment closures are effective in spatial ecology.

Keywords

dispersal rangeinteracting particle systemmoment closurepair approximationsystem of moment equations

MSC classification

Secondary: 92D40: Ecology 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Article
Information
The ANZIAM Journal , Volume 55 , Issue 1 , July 2013 , pp. 55 - 68
Copyright
Copyright ©2013 Australian Mathematical Society 

References

Anderson, K. and Neuhauser, C., “Patterns in spatial simulations—are they real?”, Ecol. Modeling 155 (2002) 19–30; doi:10.1016/S0304-3800(02)00070-4.CrossRefGoogle Scholar
Barton, N. H., Depaulis, F. and Etheridge, A. M., “Neutral evolution in spatially continuous populations”, Theor. Popul. Biol. 61 (2002) 31–48; doi:10.1006/tpbi.2001.1557.CrossRefGoogle ScholarPubMed
Bolker, B. M., “Continuous-space models for population dynamics”, in: Ecology, genetics, and the evolution of metapopulations (eds Hanski, I. and Gaggiotti, O. E.), (Elsevier Academic Press, San Diego, CA, 2004) 45–69.CrossRefGoogle Scholar
Bolker, B. M. and Pacala, S. W., “Using moment equations to understand stochastically driven spatial pattern formation in ecological systems”, Theor. Popul. Biol. 52 (1997) 179–197; doi:10.1006/tpbi.1997.1331.CrossRefGoogle ScholarPubMed
Bolker, B. M. and Pacala, S. W., “Spatial moment equations for plant competition: understanding spatial strategies and the advantages of short dispersal”, Am. Nat. 153 (1999) 575–602; doi:10.1086/303199.CrossRefGoogle ScholarPubMed
Bolker, B. M., Pacala, S. W. and Levin, S. A., “Moment methods for ecological processes in continuous space”, in: The geometry of ecological interactions: simplifying spatial complexity (eds Dieckmann, U., Law, R. and Metz, J. A. J.), (Cambridge University Press, Cambridge, 2000) 387–411.Google Scholar
Bolker, B. M., Pacala, S. W. and Neuhauser, C., “Spatial dynamics in model plant communities: what do we really know?”, Am. Nat. 162 (2003) 135–148; doi:10.1086/376575.CrossRefGoogle ScholarPubMed
Dieckmann, U., Law, R. and Metz, J. A. J., “The Geometry of Ecological Interactions: simplifying spatial complexity”, in: Cambridge studies in adaptive dynamics (Cambridge University Press, Cambridge, 2000).Google Scholar
Durrett, R., “Predator–prey systems”, in: Asymptotic problems in probability theory: stochastic models and diffusions on fractals, Volume 283 of Pitman Research notes in Mathematics (eds Elworthy, K. D. and Ikeda, N.), (Longman, Essex, UK, 1993) 37–58.Google Scholar
Durrett, R. and Levin, S., “Lessons on pattern formation from planet WATOR”, J. Theoret. Biol. 205 (2000) 201–214; doi:10.1006/jtbi.2000.2061.CrossRefGoogle ScholarPubMed
Durrett, R. and Neuhauser, C., “Particle systems and reaction–diffusion equations”, Ann. Probab. 22 (1994) 289–333; doi:10.1214/aop/1176988861.CrossRefGoogle Scholar
Etheridge, A. M., “Survival and extinction in a locally regulated population”, Ann. Appl. Probab. 14 (2004) 181–214; doi:10.1214/aoap/1075828051.CrossRefGoogle Scholar
Feller, W., An introduction to probability theory and its applications, 3rd edn, Volume 1 (John Wiley and Sons, New York, 1968).Google Scholar
Filipe, J. A. N., Maule, M. M. and Gilligan, C. A., “On ‘Analytical models for the patchy spread of plant disease.’”, Bull. Math. Biol. 66 (2004) 1027–1037; doi:10.1016/j.bulm.2003.11.001.CrossRefGoogle ScholarPubMed
Gandhi, A., Levin, S. and Orszag, S., “‘Critical slowing down’ in time-to-extinction: an example of critical phenomena in ecology”, J. Theoret. Biol. 192 (1998) 363–376; doi:10.1006/jtbi.1998.0660.CrossRefGoogle ScholarPubMed
Gandhi, A., Levin, S. and Orszag, S., “Moment expansions in spatial ecological models and moment closure through Gaussian approximation”, Bull. Math. Biol. 62 (2000) 595–632; doi:10.1006/bulm.1999.0119.CrossRefGoogle ScholarPubMed
Harada, Y. and Iwasa, Y., “Lattice population dynamics for plants with dispersing seeds and vegetative propagation”, Res. Popul. Ecol. 36 (1994) 237–249; doi:10.1007/BF02514940.CrossRefGoogle Scholar
Hausken, K. and Moxnes, J. F., “Systematization of a set of closure techniques”, Theor. Popul. Biol. 80 (2011) 175–184; doi:10.1016/j.tpb.2011.07.001.CrossRefGoogle ScholarPubMed
Hiebeler, D., “Spatially correlated disturbances in a locally dispersing population model”, J. Theoret. Biol. 232 (2005) 143–149; doi:10.1016/j.jtbi.2004.08.007.CrossRefGoogle Scholar
Iwasa, Y., “Lattice models and pair approximation in ecology”, in: The geometry of ecological interactions: simplifying spatial complexity (eds Dieckmann, U., Law, R. and Metz, J. A. J.), (Cambridge University Press, Cambridge, 2000) 227–251.CrossRefGoogle Scholar
Iwasa, Y., Nakamaru, M. and Levin, S. A., “Allelopathy of bacteria in a lattice population: competition between colicin-sensitive and colicin-producing strains”, Evol. Ecol. 12 (1998) 785–802; doi:10.1023/A:1006590431483.CrossRefGoogle Scholar
Klausmeier, C. A. and Tilman, D., “Spatial models of competition”, in: Competition and coexistence, Volume 161 of Ecological Studies (eds Sommer, U. and Worm, B.), (Springer, Berlin, Germany, 2002) 43–78.CrossRefGoogle Scholar
Krone, S. M., “Spatial models: stochastic and deterministic”, Math. Comput. Modelling 40 (2004) 393–409; doi:10.1016/j.mcm.2003.09.037.CrossRefGoogle Scholar
Law, R., Murrell, D. J. and Dieckmann, U., “Population growth in space and time: spatial logistic equations”, Ecology 84 (2003) 252–262; doi:10.1890/0012-9658(2003)084[0252:PGISAT]2.0.CO;2.CrossRefGoogle Scholar
Lewis, M. A. and Pacala, S. A., “Modeling and analysis of stochastic invasion processes”, J. Math. Biol. 41 (2000) 387–429; doi:10.1007/s002850000050.CrossRefGoogle ScholarPubMed
Matsuda, H., Ogita, N., Sasaki, A. and Satō, K., “Statistical mechanics of population—the lattice Lotka–Volterra model”, Progr. Theoret. Phys. 88 (1992) 1035–1049; doi:10.1143/PTP.88.1035.CrossRefGoogle Scholar
Murrell, D. J., Dieckmann, U. and Law, R., “On moment closure for population dynamics in continuous space”, J. Theoret. Biol. 229 (2004) 421–432; doi:10.1016/j.jtbi.2004.04.013.CrossRefGoogle ScholarPubMed
Neuhauser, C., “A long range sexual reproduction process”, Stochastic Process Appl. 53 (1994) 193–220; doi:10.1016/0304-4149(94)90063-9.CrossRefGoogle Scholar
Neuhauser, C., “The role of explicit space in plant competition models”, in: Perplexing problems in probability: festschrift in honor of Harry Kesten (progress in probability) (eds Bramson, M. and Durrett, R.), (Birkhauser, New York, 1999) 355–371.CrossRefGoogle Scholar
Neuhauser, C. and Pacala, S. W., “An explicitly spatial version of the Lotka–Volterra model with interspecific competition”, Ann. Appl. Probab. 9 (1999) 1226–1259; doi:10.1214/aoap/1029962871.CrossRefGoogle Scholar
Ovaskainen, O. and Cornell, S. J., “Asymptotically exact analysis of stochastic metapopulation dynamics with explicit spatial structure”, Theor. Popul. Biol. 69 (2006) 13–33; doi:10.1016/j.tpb.2005.05.005.CrossRefGoogle ScholarPubMed
Ovaskainen, O. and Cornell, S. J., “Space and stochasticity in population dynamics”, Proc. Natl. Acad. Sci. USA 103 (2006) 12781–12786; doi:10.1073/pnas.0603994103.CrossRefGoogle ScholarPubMed
Pacala, S. W. and Levin, S. A., “Biologically generated spatial pattern and the coexistence of competing species”, in: Spatial ecology: the role of space in population dynamics and interspecific interactions (eds Tilman, D. and Kareiva, P.), (Princeton University Press, NJ, 1998) 204–232.CrossRefGoogle Scholar
Raghib, M., Hill, N. A. and Dieckmann, U., “A multiscale maximum entropy moment closure for locally regulated in “space–time” point process models of population dynamics”, J. Math. Biol. 62 (2011) 605–653; doi:10.1007/s00285-010-0345-9.CrossRefGoogle ScholarPubMed
Rand, D. A., “Correlation equations and pair approximations for spatial ecologies”, CWI Quarterly 12 (1999) 329–368.Google Scholar
Satō, K. and Iwasa, Y., “Pair approximations for lattice-based ecological models”, in: The geometry of ecological interactions: simplifying spatial complexity (eds Dieckmann, U., Law, R. and Metz, J. A. J.), (Cambridge University Press, Cambridge, 2000) 341–358.CrossRefGoogle Scholar
Satō, K., Matsuda, H. and Sasaki, A., “Pathogen invasion and host extinction in lattice structured populations”, J. Math. Biol. 32 (1994) 251–268; doi:10.1007/BF00163881.CrossRefGoogle ScholarPubMed
Swindle, G., “A mean-field limit of the contact process with large range”, Probab. Theory Related Fields 85 (1990) 261–282; doi:10.1007/BF01277984.CrossRefGoogle Scholar
Thomson, N. A. and Ellner, S. P., “Pair-edge approximation for heterogeneous lattice population models”, Theor. Popul. Biol. 64 (2003) 271–280; doi:10.1016/S0040-5809(03)00088-1.CrossRefGoogle ScholarPubMed