Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T19:38:43.684Z Has data issue: false hasContentIssue false
  • English
  • Français

Solutions of period four for a non-linear difference equation

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theoretical Physics, Research School of Physical Sciences, Australian National University, G.P.O. Box 4, Canberra, A.C.T. 2601.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper extends earlier work by using the factorisation method to discuss solutions of period four for the difference equation

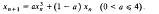
This equation was suggested by R. M. May as a simple mathematical model for the effect of frequency-dependent selection in genetics. It is shown that for a given value of the parameter, a, the identification of solutions of period four can be reduced to finding real roots for a polynomial equation of degree eight. The appropriate values of xn follow from a quartic equation. By splitting up the problem in this way it becomes relatively straightforward to determine the critical values of a at which the various solutions of period four first appear and to discuss the stability of these solutions. Intervals of stability are tabulated in the paper.

Type
Research Article
Information
The ANZIAM Journal , Volume 26 , Issue 2 , October 1984 , pp. 146 - 164
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Bôcher, M., Introduction to higher algebra (Macmillan, New York, 1907), 195–196.Google Scholar
[2]Brown, A., “Equations for periodic solutions of a logistic difference equation”, J. Austral. Math. Soc. Ser. B 23 (1981), 78–94.CrossRefGoogle Scholar
[3]Brown, A., “Solutions of period seven for a logistic difference equation”, Bull. Austral. Math. Soc. 26 (1982), 263–284.CrossRefGoogle Scholar
[4]Brown, A., “Solutions of period three for a non-linear difference equation”, J. Austral. Math. Soc. Ser. B 25 (1984), 451–462.CrossRefGoogle Scholar
[5]Griffiths, H. B., “Cayley's version of the resultant of two polynomials’, Amer. Math. Monthly 88 (1981), 328–338.CrossRefGoogle Scholar
[6]May, R. M., “Bifurcations and dynamic complexity in ecological systems”, Ann. N. Y. Acad. Sci. 316 (1979), 517–529.CrossRefGoogle Scholar
[7]May, R. M., “Non-linear problems in ecology and resource management”, Lecture Notes for Les Houches Summer School on “Chaotic behaviour of deterministic system”, July 1981.Google Scholar