ON THE SAFE STORAGE OF BAGASSE

Abstract

In this paper, we investigate the thermal evolution in a one-dimensional bagasse stockpile. The mathematical model involves four unknowns: the temperature, oxygen content, liquid water content and water vapour content. We first nondimensionalize the model to identify dominant terms and so simplify the system. We then calculate solutions for the approximate and full system. It is shown that under certain conditions spontaneous combustion will occur. Most importantly, we show that spontaneous combustion can be avoided by sequential building. To be specific, in a situation where, say, a 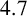$4.7\,$m stockpile can spontaneously combust, we could construct a 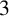$3\,$m pile and then some days later add another $1.7\,$m to produce a stable 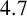$4.7\,$m pile.

1 Introduction

Bagasse is the residue which remains after sugar cane has been crushed and the majority of the juice has been extracted. In the past, it was viewed as a waste product. However, now, instead of being discarded, it is being exploited in a variety of situations. Its role as a source of biofuel has been explored in [2, 16]. After burning, the ash may be used in the manufacture of building materials [1]. The ash has also recently been employed in column adsorption technologies to remove environmental pollutants such as manganese, cobalt, copper, nickel and sulfamethoxazole from water (see [9, 14]). An obvious use is as a fuel from which to generate electricity and steam to run the sugar extraction process. This use of a local, readily available fuel reduces costs and so improves competitiveness. Unfortunately, whatever the final use of bagasse, there is a well-known problem with its storage in that large piles are prone to spontaneous combustion.

The work described in the current paper was proposed by the South African Sugar Milling Research Institute (SMRI) at the 2016 and 2017 Mathematics in Industry Study Group, and concerns the storage of bagasse for use in furnaces. Due to the safety issues, they wished to carry out a study into the processes driving spontaneous combustion. Three issues related to safe storage of bagasse were discussed at the meetings:

1. (i) calculating the maximum possible height of the bagasse heap before spontaneous combustion occurs;

2. (ii) investigating whether or not there are advantages in adjusting the moisture content; and

3. (iii) investigating whether or not there is an advantage in pelletizing the bagasse.

Preliminary results from the meetings were summarised by Myers and Mitchell [12].

Spontaneous combustion has been documented for almost 2000 years, with Pliny the Elder warning of one the many dangers associated with alcohol: “Wine-lees when dried will catch fire, and go on burning of themselves without fuel being added” [15]. The first accepted scientific study, which led to the famous van’t Hoff equation, dates back to 1844 [19]. Much of the mathematical background is described in the thesis [8] which focuses specifically on bagasse.

The first recorded bagasse spontaneous combustion incident took place in the Mourilyan stockpile in 1983. This incident motivated experiments, some of which were made by Gray et al. [5, 6], that attempted to determine why bagasse would spontaneously combust and which conditions favoured this phenomenon. Following two more ignition incidents between 1983 and 1988, Dixon [3] investigated the process of spontaneous combustion of bagasse and found that moisture content plays a very significant role in the process. Consequently, it was suggested that the effect of moisture content should never be neglected in the mathematical modelling of the spontaneous combustion of bagasse stockpiles.

Spontaneous combustion has been observed in a number of other industries such as coal mining (and the combustion of coal dust), industrial composting [11], shipping (due to flammable cargoes such as seeds, vegetable oils, cotton and coal) and in the waste recycling industry, which is a very topical example (an interesting article “Why recycling plants keep catching on fire” appeared in Time magazine in 2023 [13]). Consequently there is a rich literature on the topic. In this article, we base our work on the one-dimensional models developed by Dixon [3] and Gray and co-workers [5–7]. In the context of chemical reactors, Fowler [4] details the basic mathematical theory of thermal runaway. By focusing on the one-dimensional, we may be erring on the side of caution; being one-dimensional, the model does not account for effects (in particular, cooling) from the sides. With a narrow pile, this could result in significantly lower temperatures than predicted by a one-dimensional model. However, the conclusion of the two-dimensional numerical study of [10] suggested that the results were similar to those of an earlier one-dimensional study.

The layout of this paper is as follows. In Section 2, we give the governing equations and nondimensionalize the problem. In Section 3, we describe the numerical solution using the method of lines. In Section 4, we present results and, finally, we discuss the conclusions in Section 5.

2 Governing equations

Our mathematical study is based on the following four equations taken from [7],

(2.1) $$ \begin{align} ({\rho}_bc_b + m_w c_w W) {\frac{\partial T}{\partial t}} & = k {\frac{\partial^2 T}{\partial {x}^2}} + q_d{\rho}_bz_dX \exp\bigg(-\frac{E_d}{RT}\bigg) + q_w{\rho}_bz_wWX \exp\bigg(-\frac{E_w}{RT}\bigg) g(T) \nonumber\\ & \hspace{0.4cm} + L_v\bigg[z_cV - z_eW \exp\bigg(-\frac{L_v}{RT}\bigg)\bigg],\ \ \end{align} $$

(2.2) $$ \begin{align}\ {\frac{\partial V}{\partial t}} & = D_V {\frac{\partial^2 V}{\partial {x}^2}} + z_eW \exp\bigg(-\frac{L_v}{RT}\bigg) - z_cV,\qquad\qquad \end{align} $$

(2.3) $$ \begin{align} {\frac{\partial W}{\partial t}} & = - z_eW \exp\bigg(-\frac{L_v}{RT}\bigg) + z_cV,\qquad\qquad\qquad\quad\ \ \end{align} $$

(2.4) $$ \begin{align} \ \ \qquad\qquad\qquad{\frac{\partial X}{\partial t}} & = D_X {\frac{\partial^2 X}{\partial {x}^2}} -f{\rho}_bz_dX \exp\bigg(-\frac{E_d}{RT}\bigg)- f{\rho}_bz_wWX \exp\bigg(-\frac{E_w}{RT}\bigg) g(T), \end{align} $$

which represent the evolution of temperature T (K), water vapour V (mol/m) $^3$ , liquid water content W (mol/m $^3$ ) and oxygen X (mol/m $^3$ ) (note that we use a more natural notation for the variables than that prescribed in [7]). The notation is defined in Table 1. Equation (2.1) represents conservation of energy where the exponential terms correspond to heat sources caused by the different reactions taking place. The first exponential corresponds to a dry oxidation reaction, the second represents hydrolysis and requires both water and oxygen, while the term multiplied by $L_v$ represents the energy difference between vaporisation and condensation. A more detailed discussion of these terms and relevant assumptions is provided in [7, 18]. The function $g(T)$ is a switch that reflects the fact that the wet reaction turns off at temperature $T=T_s$ , that is,

$$ \begin{align*} g(T)=\tfrac{1}{2} [\tanh(0.6(T_s-T))+1 ] , \end{align*} $$

where $T_s$ is known through previous experimental work. Equations (2.2) and (2.3) are simple mass balances representing the temperature-driven exchange between vapour and liquid water. Theoretically, both should include diffusion but, since the vapour moves more easily, the diffusion term is only retained in (2.2). According to equations (2.2) and (2.3), vapour and water are exchanged through condensation and evaporation, where evaporation is strongly temperature dependent. Equation (2.4) shows that oxygen diffuses through the system and a significant amount is removed by oxidation and hydrolysis (it is assumed that the corresponding quantity of water is small and hence it is neglected in the mass balance (2.3), although the energy generated is nonnegligible). The many constants and typical values, taken from [7], are described in Table 1.

Table 1 Variables and parameter values for computations taken from [7].

The system is subject to the following boundary conditions. At the top surface, $x=L$ , we impose Newton cooling conditions, stating that the exchange of heat, vapour and oxygen are driven by the difference between the value in the surrounding air and the top of the pile,

(2.5) $$ \begin{align} - k {\frac{\partial T}{\partial x}} = h (T - T_a), \quad - D_V {\frac{\partial V}{\partial x}} = h_V (V - V_a), \quad - D_X {\frac{\partial X}{\partial x}} = h_X (X - X_a). \end{align} $$

Assuming that the bagasse is placed on an impermeable surface, we impose the following at $x=0$ ,

(2.6) $$ \begin{align} T = T_a, \quad {\frac{\partial V}{\partial x}} = 0, \quad {\frac{\partial X}{\partial x}} = 0. \end{align} $$

The final two conditions in (2.6) are based on the assumption that the substrate prevents vapour and water from passing through, and hence there is zero flux. The first condition assumes that, since the temperature variation is slow (of the order of days), it does not significantly affect the (infinitely large) substrate temperature and the temperatures match there. Obviously, these conditions could be altered if more precise details of the storage area were provided.

We assume that the pile is initially well mixed so that all values are constant: that is,

(2.7) $$ \begin{align} T(x,0) = T_{in},\quad V(x,0) = V_{a},\quad W(x,0) = W_{in},\quad X(x,0) = X_{a} , \end{align} $$

where subscript a refers to the ambient value. All except $W_{in}$ are known; we find this final value from the water equation below. The initial temperature differs from the ambient, since it comes from the process used to remove sugar from the bagasse and the time between processing and piling.

To simplify the problem, the equations are now written in nondimensional form. The scaling is

$$ \begin{align*} x' = \frac{x}{L}, \quad t' = \frac{t}{\Delta t} , \quad T' = \frac{T}{T_{in}}, \quad V' = \frac{V}{V_a},\quad W' = \frac{W}{\Delta W}, \quad X' = \frac{X}{X_a}, \end{align*} $$

where the time and water scales are the only ones not yet specified; we determine these below. Note that, in [18], the temperature scale is chosen from the dry reaction, ${\Delta T = E_d/R}$ . With the values provided in Table 1, this leads to $\Delta T \approx 13,000\,$ K. As this is more than twice the temperature of the Sun, we conclude that this is not representative of the process and, consequently, prefer the switch value $T_{in}$ (which is of the order of the ambient temperature). It must be the correct order of the pile temperature for most of the process. This choice also allows us to focus on the range where thermal reactions are important.

Writing equation (2.1) in nondimensional form, and immediately dropping the primes, gives

$$ \begin{align*} ({\rho}_bc_b + m_w c_w \Delta W W) \frac{T_{in}}{\Delta t} {\frac{\partial T}{\partial t}} &= \frac{kT_{in}}{L^2} {\frac{\partial^2 T}{\partial {x}^2}} + q_d{\rho}_bz_d X_aX \exp\bigg(-\frac{E_d}{RT_{in} T}\bigg) \nonumber \\ & \quad + q_w{\rho}_bz_w \Delta W X_a W X \exp\bigg(-\frac{E_w}{RT_s T}\bigg) g(T_{in} T) \nonumber \\ & \quad + L_v\bigg[z_cV_a V - z_e\Delta W W \exp\bigg(-\frac{L_v}{RT_{in} T}\bigg)\bigg]. \end{align*} $$

The quantity of primary interest in this study is the temperature, so we will work on the timescale of thermal diffusion. Balancing the left-hand side with the first term on the right-hand side leads to

$$ \begin{align*}\Delta t = \frac{L^2 \rho_b c_b }{k} = \frac{L^2}{D_T} , \end{align*} $$

where $D_{T}={k}/{\rho _b c_b }$ . Taking values from Table 1 and a $3\,$ m pile, we obtain ${\Delta t = 3.15 \times 10^6}$ s, which is approximately 36 days.

The water equation is

(2.8) $$ \begin{align} \frac{\Delta W}{\Delta t}{\frac{\partial W}{\partial t}} &= - z_e\Delta W W\exp\bigg(-\frac{L_v}{RT_{in} T}\bigg) + z_c V_a V , \end{align} $$

which makes it clear that the water scale is linked to the vapour scale, and we set

$$ \begin{align*} \Delta W = \frac{z_c V_a}{z_e} \exp\bigg(\frac{L_v}{RT_{in}}\bigg). \end{align*} $$

Again taking values from Table 1, we find $\Delta W \approx 748\,$ mol/m $^3$ . Assuming that the water concentration in the material before being placed in the pile is based on the initial temperature and vapour concentration, we choose $W_{in}=\Delta W$ . Equation (2.8) may now be written as

$$ \begin{align*} \exp\bigg(\frac{L_v}{RT_{in}}\bigg) \frac{1}{z_e\Delta t}{\frac{\partial W}{\partial t}} = - W \exp\bigg[ -\frac{L_{v}}{RT_{in}}\bigg(\frac{1}{T}-1\bigg) \bigg] + V. \end{align*} $$

With the time and water scales fixed, we may now write the full nondimensional system

(2.9) $$ \begin{align} (1+{A}_0 W) {\frac{\partial T}{\partial t}} &= {\frac{\partial^2 T}{\partial {x}^2}} + A_1 X \exp\bigg[ - \gamma _d \bigg(\frac{1}{T}-1\bigg) \bigg] + A_2 W X \exp\bigg[ - \gamma _w\bigg(\frac{1}{T}-1\bigg) \bigg] g(T) \nonumber\\ & \quad + A_3 \bigg\{ V - W \exp\bigg[ - \gamma _v \bigg(\frac{1}{T}-1\bigg) \bigg] \bigg\}, \end{align} $$

(2.10) $$ \begin{align} \quad\,\, B_0 {\frac{\partial V}{\partial t}} &= {\frac{\partial^2 V}{\partial {x}^2}} + B_1 \bigg\{ W \exp\bigg[ - \gamma _v \bigg(\frac{1}{T}-1\bigg) \bigg] - V\bigg\} ,\qquad\qquad\qquad\end{align} $$

(2.11) $$ \begin{align} \quad C_0 {\frac{\partial W}{\partial t}} &= - W \exp\bigg[ - \gamma _v\bigg(\frac{1}{T}-1\bigg) \bigg] + V,\qquad\qquad\qquad\qquad\qquad\end{align} $$

(2.12) $$ \begin{align}\qquad\quad\ \ D_0 {\frac{\partial X}{\partial t}} &= {\frac{\partial^2 X}{\partial {x}^2}} - D_1 X \exp\bigg[ - \gamma _d \bigg(\frac{1}{T}-1\bigg) \bigg]- D_2 W X \exp\bigg[ - \gamma _w \bigg(\frac{1}{T}-1\bigg) \bigg] g(T), \end{align} $$

where

$$ \begin{align*} {A}_0 &= \frac{m_w c_w W_{in}}{\rho_b c_b } , \quad A_1 = \frac{q_d{\rho}_bz_d X_aL^2}{k T_{in}} \,\exp(- \gamma _d) , \\A_2 &= \frac{q_w{\rho}_b z_w W_{in} X_a L^2}{k T_{in}}\, \exp(- \gamma _w), \quad A_3 = \frac{L_v z_c V_a L^2}{k T_{in}}, \\ B_0 &= \frac{L^2}{\Delta t D_V}, \quad B_1 = \frac{z_c L^2}{D_V} ,\quad C_0 = \frac{\exp\bigg( \gamma _v\bigg)}{z_e\Delta t} ,\\ D_0 &= \frac{L^2}{\Delta t D_X} , \quad D_1 = \frac{f{\rho}_b z_d L^2}{D_X}\,\exp(- \gamma _d) , \quad D_2 = \frac{f{\rho}_b z_w W_{in} L^2}{D_X} \,\exp(- \gamma _w), \\ \gamma _d &= \frac{E_d}{R T_{in}}, \quad \gamma _w = \frac{E_w}{R T_{in}}, \quad \gamma _v = \frac{L_v}{R T_{in}} , \end{align*} $$

and

$$ \begin{align*} g(T)=\tfrac{1}{2} [\tanh(0.6 T_{in}(T_s/T_{in}-T))+1 ]. \end{align*} $$

The boundary conditions from (2.5) become

(2.13) $$ \begin{align} - {\frac{\partial T}{\partial x}} = \alpha_T (T - T_a/T_{in}), \quad - {\frac{\partial V}{\partial x}} = \alpha_V (V - 1), \quad - {\frac{\partial X}{\partial x}} = \alpha_X (X - 1) , \end{align} $$

on $x = 1$ , where

$$ \begin{align*} \alpha_T = \frac{h L}{k}, \quad \alpha_V = \frac{h_V L}{D_V}, \quad \alpha_X = \frac{h_X L}{D_X}. \end{align*} $$

On $x = 0$ , the boundary conditions (2.6) are simply

(2.14) $$ \begin{align} T = \frac{T_a}{T_{in}}, \quad {\frac{\partial V}{\partial x}} = 0, \quad {\frac{\partial X}{\partial x}} = 0 , \end{align} $$

and the initial conditions (2.7) are

(2.15) $$ \begin{align} T(x,0) = V(x,0) = W(x,0) = X(x,0) = 1. \end{align} $$

Using values from Table 1, all coefficients from the equations and conditions may be calculated. Taking $L = 3\,$ m leads to the values presented in Table 2.

Table 2 Values of the nondimensional coefficients when $L=3\,$ m.

The high value of $A_3$ could indicate a poor balance; however, it multiplies the term representing the exchange between water and vapour. According to equation (2.3), this is of order $10^{-5}$ and so the final term of (2.1) is of order $A_3 C_0 \approx 0.6$ and the heat equation is well balanced. Similarly, although $B_1$ in (2.2) is high it also multiplies a term of order $C_0$ . The value of $B_1 C_0$ is approximately equal to $50$ , whereas $B_0 \approx 0.1$ suggests the existence of a boundary layer in V. We will discuss this later.

3 Numerical solution

We now describe the numerical solution used to provide the qualitative and approximate results. We begin by writing (2.9)–(2.12) as

(3.1) $$ \begin{align} (1 + {A}_0 W) {\frac{\partial T}{\partial t}} &= {\frac{\partial^2 T}{\partial {x}^2}} + F_T (T,V,W,X),\qquad\quad \end{align} $$

(3.2) $$ \begin{align} B_0 {\frac{\partial V}{\partial t}} &= {\frac{\partial^2 V}{\partial {x}^2}} + F_V(T,V,W),\quad\end{align} $$

(3.3) $$ \begin{align} C_0 {\frac{\partial W}{\partial t}} &= F_W(T,V,W),\qquad\qquad \end{align} $$

(3.4) $$ \begin{align} D_0 {\frac{\partial X}{\partial t}} &= {\frac{\partial^2 X}{\partial {x}^2}} + F_X(T,V,W,X), \end{align} $$

respectively, and solve this system using the method of lines of Schiesser [17]. We define the spatial mesh $x_i = i\Delta x$ for $i = 0,\,1,\,\ldots ,\,I$ , where $\Delta x = 1/I$ and let $T_i = T(x_i,t)$ ; similarly for $V_i$ , $W_i$ and $X_i$ . Then we discretize the diffusion terms in (3.1)–(3.2) and (3.4) as

$$ \begin{align*} (1 + {A}_0 W_i) \frac{d T_i}{d t} &= \frac{T_{i+1} - 2 T_i + T_{i-1}}{\Delta x^2} + F_T (T_i,V_i,W_i,X_i), \\ B_0 \frac{d V_i}{d t} &= \frac{V_{i+1} - 2 V_i + V_{i-1}}{\Delta x^2} + F_V(T_i,V_i,W_i) , \\ D_0 \frac{d X_i}{d t} &= \frac{X_{i+1} - 2 X_i + X_{i-1}}{\Delta x^2} + F_X(T_i,V_i,W_i,X_i), \end{align*} $$

for $i = 1,\,2,\,\ldots ,\,I-1$ . Equation (3.3) is simply

$$ \begin{align*} C_0 \frac{d W_i}{d t} = F_W(T_i,V_i,W_i),\end{align*} $$

which holds for $i= 0,\,1,\,\ldots ,\,I$ . The first boundary condition in (2.14) on $x = 0$ immediately gives $T_0 = T_{in}/T_s$ . For the other remaining conditions in (2.14) and for those in (2.13) on $x = 1$ , we obtain further ordinary differential equations (ODEs) involving $V_0$ , $X_0$ , $T_{I}$ , $V_{I}$ and $X_{I}$ . These are

$$ \begin{align*} B_0 \frac{d V_0}{d t} &= \frac{2(V_{1} - V_0)}{\Delta x^2} + F_V(T_0,V_0,W_0), \\[2.5pt]D_0 \frac{d X_0}{d t} &= \frac{2(X_{1} - X_0) }{\Delta x^2} + F_X(T_0,V_0,W_0,X_0),\\[2.5pt](1 + {A}_0 W_I) \frac{d T_I}{d t} &= \frac{2\big( T_{I-1} - T_I - \Delta x \,\alpha_T (T_I-T_a/T_s)\big)}{\Delta x^2} + F_T (T_I,V_I,W_I,X_I), \\[2.5pt]B_0 \frac{d V_I}{d t} &= \frac{2\big(V_{I-1} - V_I - \Delta x\,\alpha_V (V_I - 1)\big)}{\Delta x^2} + F_V(T_I,V_I,W_I), \\[2.5pt]D_0 \frac{d X_I}{d t} &= \frac{2\big(X_{I-1} - X_I - \Delta x\,\alpha_X (X_I -1)\big)}{\Delta x^2} + F_X(T_I,V_I,W_I,X_I). \end{align*} $$

This system of ODEs is solved, with the initial conditions in (2.15), using ode23s in Matlab.

3.1 Reduced model

Based on the size of certain coefficients involved in the model, we also analyse a reduced system where W is taken as steady state (this is clearly justifiable since $C_0 = 2.9 \times 10^{-5}$ ). Thus, we set

$$ \begin{align*}W = V \exp(\gamma_v (1/T-1)) .\end{align*} $$

Consistent with this steady-state solution, the vapour equation indicates $V_{xx} \approx 0$ which leads to $V = 1$ .

The numerical solution now depends purely on equations (3.1) and (3.4) where, in keeping with the steady-state W solution, we neglect the $A_3$ term in (3.1) and replace $W = \exp (\gamma _v (1/T-1)) $ in (3.4). This two-equation system is compared with the four-equation system in the following section.

4 Results

In Figure 1(a) and (b) we show the numerical solution of the full system for the dimensional temperature and vapour distribution in a $3\,$ m pile after 50 days. Given our focus on spontaneous combustion, the temperature is the quantity of primary interest. From Figure 1(a) we can see that, so far, this pile gives no indication of thermal runaway. The initial constant temperature, $T_{in}=65^\circ $ C, very quickly reduces to a smoothly curved profile satisfying the fixed temperature condition $T= 30^\circ $ C at $x=0$ . The maximum temperature remains just below 60 $^\circ $ C for almost the whole time period. After the initial transient period, the vapour, shown in Figure 1(b), has a central approximately constant region, as suggested by the reduced model, but with boundary layers at either end where it adjusts to the upper and lower boundary conditions. Liquid water, shown in Figure 2(a), builds up slightly at the substrate, where it cannot escape, and more so at the top surface where vapour from the air arrives and condenses. Mathematically, we note that, in the steady-state approximation, $W \approx V $ , and then the high value near the surface corresponds to the boundary layer of V. Finally, Figure 2(b) shows the oxygen content, which obviously decreases away from the top surface as it is used by the thermal reaction.

Figure 1 (a) Temperature in $3\,$ m pile after 50 days; and (b) corresponding vapour distribution.

Figure 2 (a) Water distribution in $3\,$ m pile; and (b) oxygen distribution.

In Figure 3(a), we present a comparison between the maximum temperature profiles (against time) for the four- and two-equation models, for three values of pile thickness. For the $4\,$ m, $4\,$ m piles, the two sets of curves are very close. Crucially the models exhibit almost identical maximum temperatures, which suggests that the two-equation model can provide a good approximation to the full model. This is slightly surprising, since the reduction is based on the assumption that V is constant; in dimensional form $V=V_a$ . Yet the solution of the full model, Figure 1(b), shows clearly that V is only close to the ambient value in the top $2\,$ m of the pile. In the bottom metre, it reduces by almost a factor of three. A possible reason why this error does not affect the temperature is that heat is primarily generated away from the bottom region: it is generated where the oxygen level is high. Consequently, although the vapour approximation is inaccurate near the substrate, the fact that it is more accurate where heat is generated results in a good approximation to the overall temperature profile. For the case $L=5\,$ m, both solutions have blown up and no solution was found for the two-equation system.

Figure 3 (a) A comparison of the maximum temperature profiles (against time) for the two-equation model (in red) and for the full four-equation model (in black), for three values of L; and (b) three values of L near runaway for the four-equation model (colour available online).

In Figure 3(b), we examine the region approaching blow-up in more detail using the four-equation model (which turned out to be more stable). For the two cases ${L=4.6\,}$ m and $L=4.65\,$ m, the temperature peaks and then slowly decreases. Switching to $L=4.7\,$ m, the gradient is initially high, and then reduces at around three days but continues to slowly increase, ultimately leading to thermal runaway. If we continued the calculation beyond 20 days this would become more apparent. Hence, in this case, the switch in stability occurs somewhere between $L = 4.65\,$ m and $L = 4.70\,$ m and, for piles higher than this, switch thermal runaway will occur. Note that this type of system typically has three theoretical steady-state solutions; here we have followed the path to the lower value, which is the most physically relevant.

Finally, in Figure 4, we focus on the crucial region with $L=4.6\,$ m and $L= 4.7\,$ m, and demonstrate a possible way forward for the storage of combustible materials. Figure 4(a) shows the temperature evolution of a $4.6\,$ m pile. The solid line corresponds to the dashed line of Figure 3(b), which takes its maximum value just before six days. In comparison, the dashed line here shows the result when a $3\,$ m pile is laid down and then, after one day, a $1.6\,$ m layer is added on top. It appears that, at this time, the temperature is just peaking and the reaction is slowing down. The temperature then reduces until around day two when the interaction with the upper layer results in a second peak. After 20 days the temperature is approximately 8 $^\circ $ C below that of the single $4.6\,$ m pile. This is more than enough to prevent thermal runaway. The dash-dot line shows the result for a $4\,$ m and a $0.6\,$ m combination. In this case, no secondary peak occurs. This results in a final reduction of around 5 $^\circ $ C below the single pile temperature. Although $L=4.6\,$ m is stable, it demonstrates that building the pile sequentially does give a much reduced maximum temperature, because a significant quantity of the initial heat is allowed to escape. This can provide a margin of error.

Figure 4 A comparison of the maximum temperature profiles against time for a single layer and for two layers (obtained by sequential building), for (a) $L = 4.6\,$ m; and (b) $L = 4.7\,$ m (colour available online).

With an interest in the runaway in Figure 4(b), we show results for a final height of $4.7\,$ m. The solid line repeats the result of Figure 3(b). The dashed line represents the pile made through the $3\,$ m and $1.7\,$ m combination. Again a secondary peak occurs and now the difference in temperatures after 20 days is almost 20 $^\circ $ C. Clearly, this sequentially built pile is cooling down rather than moving towards combustion. The dash-dot line, representing a $4\,$ m and $0.7\,$ m combination, results in an approximately 14 $^\circ $ C reduction after 20 days, also avoiding combustion. Hence, we conclude that sequential building seems to be the answer: even if there is only a short time between adding the second pile, it is enough to prevent thermal runaway.

5 Conclusion

In this report, we have presented a mathematical model for a one-dimensional bagasse stockpile, coupling the effects of temperature, liquid water, water vapour and oxygen. The numerical solution of this system shows that it is capable of predicting thermal runaway.

The full model investigated involved four variables: temperature, water content, vapour content and oxygen content. However, a reduced system involving solving for only temperature and oxygen showed excellent agreement with the full model, although, tests did show that the two-equation model would predict runaway at slightly earlier times. Previous work suggested that the water content must be included; our result does not contradict this, but it merely states that the water follows a pseudo-steady state with a simple variation due to temperature changes. This observation could be exploited to permit a more analytical examination of the behaviour.

The most significant conclusion from this study concerns the strategy for building large piles without leading to ignition. Specifically, if we build a pile sequentially, we can avoid spontaneous combustion. In our calculations, we found that, under the prescribed conditions, thermal runaway occurred for piles greater than somewhere between $4.65\,$ m and $4.7\,$ m. By first building a $3\,$ m pile and then adding another $1.7\,$ m layer, the temperature around the critical point was reduced by some 10 $^\circ $ C when compared with a $4.7\,$ m pile, and after 20 days this changed to around 20 $^\circ $ C as the single pile started its journey to thermal runaway. Of course, we could continue this strategy to make larger piles, with more layers, but with this single example we have paved the way for a more complete investigation.

This brings us to the main question proposed by the SMRI. How high can a bagasse pile be built without spontaneous combustion occurring? The answer depends crucially on the method of building. A $5\,$ m pile laid down in a single go could ignite, whereas a pile made up of a $3\,$ m one followed by a $2\,$ m one may not, even if there is only a single day between adding the second layer. Multiple-layer piles could be significantly higher than single-layer piles. So, there is no simple answer to the question posed by the SMRI. However, there is a clear recommendation: build sequentially, to allow the initial heat to escape, which will result in thermally stable piles.