Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-04T09:22:19.810Z Has data issue: false hasContentIssue false
  • English
  • Français

On stability and stationary points in nonlinear optimization

Published online by Cambridge University Press:  17 February 2009

J. Guddat ,
H. Th. Jongen  and
J. Rueckmann
J. Guddat
Affiliation:
Humboldt-University, Berlin, German Democratic Republic
H. Th. Jongen
Affiliation:
Twente University of Technology, Enschede, The Netherlands
J. Rueckmann
Affiliation:
Technical University Leipzig, Leipzig, German Democratic Republic
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents three theorems concerning stability and stationary points of the constrained minimization problem:

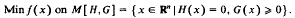
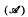In summary, we prove that, given the Mangasarian-Fromovitz constraint qualification (MFCQ), the feasible set M[H, G] is a topological manifold with boundary, with specified dimension; (ℬ) a compact feasible set M[ H, G] is stable (perturbations of H and G produce homeomorphic feasible sets) if and only if MFCQ holds; 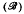under a stability condition, two lower level sets of f with a Kuhn-Tucker point between them are homotopically related by attachment of a k-cell (k being the stationary index in the sense of Kojima).

Type
Research Article
Information
The ANZIAM Journal , Volume 28 , Issue 1 , July 1986 , pp. 36 - 56
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Bank, B., Guddat, J., Klatte, D., Kummer, B. and Tammer, K., Non-linear parametric optimization (Akademie-Verlag, Berlin, 1982).CrossRefGoogle Scholar
[2]Dontchev, A. L. and Jongen, H. Th., “On the regularity of the Kuhn-Tucker curve”, SIAM J. Control Optim. (to appear), (Preprint No. 460, Twente University of Technology (1984)).Google Scholar
[3]Fiacco, A. V. and Kyparisis, J., “Sensitivity analysis in nonlinear programming under second order assumptions”, in Systems and Optimization, Lect. Notes in Control and Inf. sciences, Vol. 66 (eds. Bagchi, A. and Jongen, H. Th.) (1985), 74–97.Google Scholar
[4]Fiacco, A. V. and McCormick, G. P., Nonlinear programming: Sequential unconstrained minimization techniques (Wiley, New York, 1968).Google Scholar
[5]Gauvin, J., “A necessary and sufficient regularity condition to have bounded multipliers in nonconvex programming”, Math. Programming 12 (1977), 136–138.CrossRefGoogle Scholar
[6]Hager, W. W., “Lipschitz continuity for constrained processes”, SIAM J. Control Optim. 17 (1979), 321–338.CrossRefGoogle Scholar
[7]Hettich, R. and Jongen, H. Th., “On first and second order conditions for local optima for optimization problems in finite dimensions”, Methods of Operations Research Vol. 23 (1977), 82–97.Google Scholar
[8]Hirsch, M. W., Differential topology (Springer-Verlag, 1976).CrossRefGoogle Scholar
[9]Hurewicz, W., Lectures on ordinary differential equations (The M. I. T. Press, 1958).CrossRefGoogle Scholar
[10]Jongen, H. Th., Jonker, P. and Twilt, F., “On one-parameter families of sets defined by (in)equality constraints”, Nieuw Arch. Wisk. (3), 30 (1982), 307–322.Google Scholar
[11]Jongen, H. Th., Jonker, P. and Twilt, F., Non-linear optimization in Rn, I. Morse theory, Chebyshev approximation (Peter Lang Verlag, Frankfurt a. M., Bern, New York, 1983).Google Scholar
[12]Jongen, H. Th., Jonker, P. and Twilt, F., “One-parameter families of optimization problems: Equality constraints”, J. Optim. Theory Appl. 48 (1986), 141–161.CrossRefGoogle Scholar
[13]Jongen, H. Th., Jonker, P. and Twilt, F., “Critical sets in parametric optimization”, Math. Programming 35 (1986), 1–21.Google Scholar
[14]Jongen, H. Th., Jonker, P. and Twilt, F., “ Nonlinear optimization theory in Rn from a global point of view V”, Twente University of Technology, Preprint No. 462 (1984).Google Scholar
[15]Jongen, H. Th., Jonker, P. and Twilt, F., “Nonlinear optimization theory in Rn from a global point of view VI”, Twente University of Technology, Preprint No. 506 (1985).Google Scholar
[16]Jongen, H. Th., Jonker, P. and Twilt, F., Nonlinear optimization in Rn; II. Transuersality, flows, parametric aspects (forthcoming, to appear in Peter Lang Verlag).Google Scholar
[17]Kojima, M., “Strongly stable stationary solutions in nonlinear programs”, in Analysis and computation of fixed points (ed. Robinson, S. M.), (Academic Press, New York, 1980), 93–138.CrossRefGoogle Scholar
[18]Kojima, M. and Hirabayashi, R., “Continuous deformation of nonlinear programs”, Math. Programming Stud. 21 (1984), 150–198.CrossRefGoogle Scholar
[19]Levitin, E. S. (E. C. ЛеВИтИн), “O коррекцин решеии залау нелинеинеиноо программирования с непольнои инφормацин”, Всесоюзная летняя школа о метолаξ оцтимизации и иξ дрименении (Akad. Nauk SSSR, Sib. Otdel, Irkutsk, 1974 (I, II)).Google Scholar
[20]Milnor, J., Morse theory, Annals of Mathematics Studies No. 51 (Princeton University Press, 1963).CrossRefGoogle Scholar
[21]Palais, R. S. and Smale, S., “A generalized Morse theory”, Bull. Amer. Math. Soc. 70 (1964), 165–172.CrossRefGoogle Scholar
[22]Robinson, S. M., “Stability theory for systems of inequalities, part II: differentiable nonlinear systems”, SIAM J. Numer. Anal. Vol. 13, No. 4 (1976), 497–513.CrossRefGoogle Scholar
[23]Schecter, S., “Structure of the first order solution set for a class of nonlinear programs with parameters”, Math. Programming 34 (1986), 84–110.CrossRefGoogle Scholar
[24]Spanier, E. H., Algebraic topology (McGraw-Hill, Inc., 1966).Google Scholar