Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T05:46:05.888Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MULTI-ASSET SPREAD OPTION PRICING IN A WICK–ITÔ–SKOROHOD INTEGRAL FRAMEWORK

Part of: Harmonic analysis in several variables Mathematical finance Stochastic analysis

Published online by Cambridge University Press:  24 May 2017

XIANGXING TAO Open the ORCID record for XIANGXING TAO [Opens in a new window]  and
YAFENG SHI
XIANGXING TAO*
Affiliation:
School of Science, Zhejiang University of Science and Technology, Hangzhou, 310023, PR China email [email protected]
YAFENG SHI
Affiliation:
School of Science, Ningbo University of Technology, Ningbo, 315211, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide an elementary method for exploring pricing problems of one spread options within a fractional Wick–Itô–Skorohod integral framework. Its underlying assets come from two different interactive markets that are modelled by two mixed fractional Black–Scholes models with Hurst parameters, 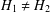$H_{1}\neq H_{2}$, where 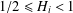$1/2\leq H_{i}<1$ for 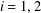$i=1,2$. Pricing formulae of these options with respect to strike price 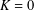$K=0$ or 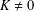$K\neq 0$ are given, and their application to the real market is examined.

Keywords

fractional stochastic equationspread optionBlack–Scholes marketfractional Itô formula

MSC classification

Primary: 60H30: Applications of stochastic analysis (to PDE, etc.)
Secondary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.) 91G20: Derivative securities 91G80: Financial applications of other theories (stochastic control, calculus of variations, PDE, SPDE, dynamical systems)
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 3-4 , April 2017 , pp. 386 - 396
Copyright
© 2017 Australian Mathematical Society 

References

Biagini, F., Hu, Y., Øksendal, B. and Zhang, T., Stochastic calculus for fractional Brownian motion and applications (Springer, London, 2008).CrossRefGoogle Scholar
Bianchi, S., Pantanella, A. and Pianese, A., “Modeling stock prices by multifractional Brownian motion: an improved estimation of the pointwise regularity”, Quant. Finance 11 (2011) 1–14; doi:10.1080/14697688.2011.594080.Google Scholar
Caldana, R. and Fusai, G., “A general closed-form spread option pricing formula”, J. Banking Finance 37 (2013) 4893–4906; http://dx.doi.org/10.1016/j.jbankfin.2013.08.016.Google Scholar
Carmona, R. and Durrleman, V., “Pricing and hedging spread options”, SIAM Rev. 45 (2003) 627–685; http://dx.doi.org/10.1137/S0036144503424798.CrossRefGoogle Scholar
Carr, P. and Madan, D., “Option valuation using the fast Fourier transform”, J. Comput. Finance 2 (1999) 61–73; http://dx.doi.org/10.21314/JCF.1999.043.Google Scholar
Dempster, M. and Hong, S., “Spread option valuation and the fast Fourier transform”, Math. Finance Bachelier Congr. 1 (2000) 203–220; http://dx.doi.org/10.1007/978-3-662-12429-1-10.Google Scholar
Deng, S., Li, M. and Zhou, J., “Closed-form approximations for spread option prices and Greeks”, J. Derivatives 16 (2008) 58–80.Google Scholar
Elliott, R. J. and Van der Hoek, J., “A general fractional white noise theory and applications to finance”, Math. Finance 13 (2003) 301–330; http://dx.doi.org/10.1111/1467-9965.00018.CrossRefGoogle Scholar
Fama, E. F., “The behaviour of stock market prices”, J. Bus. 38 (1965) 34–105; http://www.e-m-h.org/Fama65.pdf.Google Scholar
Hu, Y. and Øksendal, B., “Fractional white noise calculus and applications to finance”, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 6 (2003) 1–32; http://dx.doi.org/10.1142/S0219025703001110.Google Scholar
Hurd, T. R. and Zhou, Z., “A Fourier transform method for spread option pricing”, SIAM J. Financial Math. 1 (2010) 142–157; http://dx.doi.org/10.1137/090750421.Google Scholar
Li, M., Zhou, J. and Deng, S. J., “Multi-asset spread option pricing and hedging”, Quant. Finance 10 (2010) 305–324; http://dx.doi.org/10.1080/14697680802626323.Google Scholar
Lo, A. W. and MacKinley, A. C., “Stock market prices do not follow random walks: Evidence from a simple specification test”, Rev Financ Stud. 1 (1988) 41–66; http://dx.doi.org/10.1093/rfs/1.1.41.Google Scholar
Necula, C., “Option pricing in a fractional Brownian motion environment”, SSRN Electronic J. 6 (2002) 258–273 ; http://dx.doi.org/10.2139/ssrn.1286833.Google Scholar
Peters, E., Fractal market analysis applying chaos theory to investment and economics (John Wiley & Sons Inc., Berlin, 2002).Google Scholar
Ravindran, K., “Low-fat spreads”, Risk 6 (1993) 56–57.Google Scholar
Rostek, S., Option pricing in fractional Brownian markets (Springer, New York, 2009).Google Scholar
Shimko, D., “Options on futures spreads: hedging, speculation and valuation”, J. Futures Mark. 14 (1994) 183–213; http://dx.doi.org/10.1002/fut.3990140206.CrossRefGoogle Scholar
Tao, X.-X. and Shi, Y.-F., “Option pricing on fractional correlated stocks”, Manag. Eng. Appl. 2010 (2010) 539–545.Google Scholar