Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-02T20:37:00.217Z Has data issue: false hasContentIssue false
  • English
  • Français

On a direct method for the determination of an exact invariant for the time-dependent harmonic oscillator

Published online by Cambridge University Press:  17 February 2009

P. G. L. Leach
P. G. L. Leach
Affiliation:
Department of Mathematics, La Trobe University, Bandoora, Vic. 3083, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

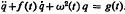An exact invariant is found for the one-dimensional oscillator with equation of motion . The method used is that of linear canonical transformations with time-dependent coeffcients. This is a new approach to the problem and has the advantage of simplicity. When f(t) and g(t) are zero, the invariant is related to the well-known Lewis invariant. The significance of extension to higher dimension of these results is indicated, in particular for the existence of non-invariance dynamical symmetry groups.

Type
Research Article
Information
The ANZIAM Journal , Volume 20 , Issue 1 , June 1977 , pp. 97 - 105
Copyright
Copyright © Australian Mathematical Society 1977

References

[1]Boon, M. H. and Seligman, T. H., “Canonical transformations applied to the free Landau electron”, J. Math. Phys. 14 (1973), 1224–1227.CrossRefGoogle Scholar
[2]Boyer, C. P. and Wolf, K. B., “Canonical transforms. III. Configuration and phase descriptions of quantum systems possessing and sl(2, R) dynamical algebra”, J. Math. Phys. 16 (1975), 1493–1502.CrossRefGoogle Scholar
Katzin, G. H. and Levine, J., “Dynamical symmetries and constans of the motion for classical particle systems”, J. Math. Phys. 15 (1974), 1460–1470.CrossRefGoogle Scholar
Kohler, R. H., “Extended view of classical contact transformations”, Foundations of Physics 6 (1976), 193–208.CrossRefGoogle Scholar
Louck, J. D., Moshinsky, M. and Wolf, K. B., “Canonical transformations and accidental degeneracy. I. The anisotropic oscillator”, J. Math. Phys. 14 (1973), 692–695.CrossRefGoogle Scholar
Moshinsky, M., “Canonical transformations and quantum mechanics”, SIAM J. Appl. Math. 25 (1973), 193–212.CrossRefGoogle Scholar
Moshinsky, M. and Patera, J., “Canonical transformations and accidental degeneracy. IV. Problems with continuous spectra”, J. Math. Phys. 16 (1975), 1866–1875.CrossRefGoogle Scholar
Moshinsky, M. and Quesne, C., “Linear canonical transformations and their unitary representations”, J. Math. Phys. 12 (1971), 1272–1283.CrossRefGoogle Scholar
[2]Wolf, K. B., “Canonical transforms. I. Complex linear tranforms”, J. Math. Phys. 15 (1974), 1295–1301.CrossRefGoogle Scholar
[3]Eliezer, C. J. and Gray, A., “A note on the time-dependent harmonic oscillator”, SIAM J. Appl. Math. 30 (1976), 463–468.CrossRefGoogle Scholar
[4]Günther, N. J. and Leach, P. G. L., “Generalized invariants for the time-dependent harmonic oscillator”, J. Math. Phys. 18 (1977), 572–576.CrossRefGoogle Scholar
[5]Ince, E. L., Ordinary Different Equations pp.71, 72, Dover, New York (1956).Google Scholar
[6]Kruskal, M., “Asymptotic theory of Hamiltonian and other systems with all solutions nearly periodic”, J. Math. Phys. 3 (1962), 806–828.CrossRefGoogle Scholar
[7]Leach, P. G. L., “On the theory of time-dependent linear canonical transformations as applied to Hamiltonians of the harmonic oscillator-type”, La Trobe University Department of Mathematics preprint (to appear in J. Math. Phys.).Google Scholar
[8]Leach, P. G. L., “Invariants and wave-functions for some time-dependent harmonic oscillator-type Hamiltonians”, La Trobe University Department of Mathematics preprint.Google Scholar
[9]Leach, P. G. L., “Quadratic Hamiltonians, quadratic invariants and the symmetry group SU(n)”, La Trobe University Department of Mathematics preprint.Google Scholar
[10]Lewis, H. R., “Classical and quantum systems with time-dependent harmonic oscillator-type Hamiltonians”, Phys. Rev. Letters 18 (1967), 510–512.CrossRefGoogle Scholar
[11]Lewis, H. R. Jr, “Motion of a time-dependent harmonic oscillator and of a charged particle in a class of time-dependent axially symmetric electromagnetic fields”, Phys. Rev. 172 (1968), 1313–1315.CrossRefGoogle Scholar
[12]Lewis, H. R. Jr, “Class of exact invariants for classical and quantum time-dependent harmonic oscillators”, J. Math. Phys. 9 (1968), 1976–1986.CrossRefGoogle Scholar
[13]Lewis, H. R. Jr and Riesenfeld, W. B., “An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field”, J. Math. Phys. 10 (1969), 1458–1473.CrossRefGoogle Scholar
[14]Mukunda, N., O'Raifeartaigh, L. and Sudarshan, E. C. G., “Characteristic non-invariance groups of dynamical systems”, Phys. Rev. Letters 15 (1965), 1041–1044.CrossRefGoogle Scholar
[15]Pars, L. A., A Treatise on Analytical Dynamics, p. 500, Heinemann, London (1965).Google Scholar
[16]Pinney, E., “The non-linear differential equation yn + p(x) y + Cy −3 = 0”, Proc. Amer. Math. Soc. 1 (1950), 681.Google Scholar
[17]Sarlet, W., “Class of Hamiltonians with one-degree-of-freedom allowing application of Kruskal's asymptotic theory in closed form I”, Annals of Phys. 92 (1975), 232–267.CrossRefGoogle Scholar
[18]Sarlet, W., “Class of Hamiltonians with one-degree-of-freedom allowing application of Kruskal's asymptotic theory in closed form II”, Annals of Phys. 92 (1975), 248–261.CrossRefGoogle Scholar
[19]Seymour, P. W., “Motions of charged particles in plasmas”, Int. J. Engng. Sci. 1 (1963), 423–451.CrossRefGoogle Scholar
[20]Seymour, P. W., Leipnik, R. B. and Nicholson, A. F., “Charged particle motion in a time-dependent axially symmetric magnetic field”, Aust. J. Phys. 18 (1965), 553–565.CrossRefGoogle Scholar
[21]Sudarshan, E. C. G., Mukunda, N. and O'Raifeartaigh, L., “Group theory of the Kepler problem”, Phys. Lett. 19 (1965), 322–325.CrossRefGoogle Scholar
[22]Symon, K. R., “The adiabatic invariance of the linear or non-linear oscillator”, J. Math. Phys. 11 (1970), 1320–1330.CrossRefGoogle Scholar
[23]Wolf, K. B., “Canonical transforms, separation of variables and similarity solutions for a class of parabolic differential equations”, J. Math. Phys. 17 (1976), 601–613.CrossRefGoogle Scholar