Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-04T10:02:01.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-classical integrals of Bessel functions

Published online by Cambridge University Press:  17 February 2009

S. N. Stuart
S. N. Stuart
Affiliation:
C.S.I.R.O. Division of Chemical Physics, P. O. Box 160, Clayton, Victoria 3168
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Certain definite integrals involving spherical Bessel functions are treated by relating them to Fourier integrals of the point multipoles of potential theory. The main result (apparently new) concerns

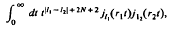
where l1, l2 and N are non-negative integers, and r1 and r2 are real; it is interpreted as a generalized function derived by differential operations from the delta function δ(r1 − r2). An ancillary theorem is presented which expresses the gradient ∇2nYlm(∇) of a spherical harmonic function g(r)YLM(Ω) in a form that separates angular and radial variables. A simple means of translating such a function is also derived.

Type
Research Article
Information
The ANZIAM Journal , Volume 22 , Issue 3 , January 1981 , pp. 368 - 378
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Bayman, B. F., “A generalization of the spherical harmonic gradient formula”, J. Math. Phys. 19 (1978), 2558–2562.CrossRefGoogle Scholar
[2]Brink, D. M. and Satchler, O. R., Angular momentum (Clarendon Press, Oxford, 2nd edition, 1968).Google Scholar
[3]Fano, U. and Racah, G., Irreducible tensorial sets (Academic Press, 1959).Google Scholar
[4]Hobson, E. W., The theory of spherical and ellipsoidal harmonics (Cambridge University Press, 1931).Google Scholar
[5]Jackson, A. D. and Maximon, L. C., “Integrals of products of Bessel functions”, SIAM J. Math. Anal. 3 (1972), 446–460.CrossRefGoogle Scholar
[6]Jette, A. N., “A convenient method for evaluating two centre integrals”, Internal. J. Quantum Chem. 7 (1973), 131–132, 1040.CrossRefGoogle Scholar
[7]Jones, D. S., Generalised functions (McGraw-Hill, 1966).Google Scholar
[8]Kay, K. G., Todd, H. D. and Silverstone, H. J., “Dirac delta functions in the Laplace-type expansion of (θ, φ)”, J. Chem. Phys. 51 (1969), 2359–2362.CrossRefGoogle Scholar
[9]Messiah, A., Quantum mechanics (North Holland, 1961).Google Scholar
[10]Miller, W., Lie theory and special functions (Academic Press, 1968).Google Scholar
[11]Milleur, M. B., Twerdochlib, M. and Hirschfelder, J. O., “Bipolar angle averages and two-centre, two-particle integrals involving r 12”, J. Chem. Phys. 45 (1966), 13–20.CrossRefGoogle Scholar
[12]Prosser, F. P. and Blanchard, C. H., “On the evaluation of two-centre integrals”, J. Chem. Phys. 36 (1962), 1112; 43 (1965), 1086.CrossRefGoogle Scholar
[13]Rowe, E. G. P., “Spherical delta functions and multipole expansions”, J. Math. Phys. 19 (1978), 1962–1968.CrossRefGoogle Scholar
[14]Ruedenberg, K., “Bipolare Entwicklungen, Fourier-transformation und molekulare Mehrzentren-Integrale”, Theorel. Chim. Ada 7 (1967), 359–366.CrossRefGoogle Scholar
[15]Sack, R. A., “Generating functions for spherical harmonics: part I, three-dimensional harmonics”, SIAM J. Math. Anal. 5 (1974), 774–796.CrossRefGoogle Scholar
[16]Santos, F. D., “Finite range approximations in direct transfer reactions”, Nucl. Phys. A212 (1973), 341–364.CrossRefGoogle Scholar
[17]Silverstone, H. J., “Expansion about an arbitrary point of three-dimensional functions involving spherical harmonics by the Fourier-transform convolution theorem”, J. Chem. Phys. 47 (1967), 537–540.CrossRefGoogle Scholar
[18]Sneddon, I. N., Fourier transforms (McGraw-Hill, 1951).Google Scholar
[19]Stratton, J. A., Electromagnetic theory (McGraw-Hill, 1941).Google Scholar
[20]Suzuki, Y., “Some formulae on Bessel and Legendre functions”, J. Coll. Arts Sci. Chiba Univ. 3 (1962), 441–446.Google Scholar
[21]Watson, G. N., A treatise on the theory of Bessel functions (Cambridge University Press, 2nd edition 1944).Google Scholar