Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T23:08:16.474Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW APPROACH TO SELECT THE BEST SUBSET OF PREDICTORS IN LINEAR REGRESSION MODELLING: BI-OBJECTIVE MIXED INTEGER LINEAR PROGRAMMING

Part of: Linear inference, regression Operations research and management science

Published online by Cambridge University Press:  11 January 2019

HADI CHARKHGARD Open the ORCID record for HADI CHARKHGARD [Opens in a new window]  and
ALI ESHRAGH Open the ORCID record for ALI ESHRAGH [Opens in a new window]
HADI CHARKHGARD*
Affiliation:
Department of Industrial and Management Systems Engineering, University of South Florida, Tampa, FL 33620, USA email [email protected]
ALI ESHRAGH
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, New South Wales 2308, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the problem of choosing the best subset of 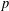$p$ features in linear regression, given $n$ observations. This problem naturally contains two objective functions including minimizing the amount of bias and minimizing the number of predictors. The existing approaches transform the problem into a single-objective optimization problem. We explain the main weaknesses of existing approaches and, to overcome their drawbacks, we propose a bi-objective mixed integer linear programming approach. A computational study shows the efficacy of the proposed approach.

Keywords

linear regressionbest subset selectionbi-objective mixed integer linear programming

MSC classification

Primary: 62J05: Linear regression
Secondary: 90B50: Management decision making, including multiple objectives 90C11: Mixed integer programming
Type
Research Article
Information
The ANZIAM Journal , Volume 61 , Issue 1 , January 2019 , pp. 64 - 75
Copyright
© 2019 Australian Mathematical Society 

References

Bertsimas, D., King, A. and Mazumder, R., “Best subset selection via a modern optimization lens”, Ann. Statist. 44 (2016) 813–852; doi:10.1214/15-AOS1388.Google Scholar
Bickel, P. J., Ritov, Y. and Tsybakov, A. B., “Simultaneous analysis of Lasso and Dantzig selector”, Ann. Statist. 37 (2009) 1705–1732; doi:10.1214/08-AOS620.Google Scholar
Boland, N., Charkhgard, H. and Savelsbergh, M., “A criterion space search algorithm for biobjective integer programming: the balanced box method”, INFORMS J. Comput. 27 (2015) 735–754; doi:10.1287/ijoc.2015.0657.Google Scholar
Boland, N., Charkhgard, H. and Savelsbergh, M., “A criterion space search algorithm for biobjective mixed integer programming: the triangle splitting method”, INFORMS J. Comput. 27 (2015) 597–618; doi:10.1287/ijoc.2015.0646.Google Scholar
Candés, E. J. and Plan, Y., “Near-ideal model selection by $l_{1}$ minimization”, Ann. Statist. 37 (2009) 2145–2177; doi:10.1214/08-AOS653.Google Scholar
Chankong, V. and Haimes, Y. Y., Multiobjective decision making: theory and methodology (Elsevier Science, New York, 1983).Google Scholar
Chen, S. S., Donoho, D. L. and Saunders, M. A., “Atomic decomposition by basis pursuit”, SIAM J. Sci. Comput. 20 (1998) 33–61; doi:10.1137/S1064827596304010.Google Scholar
Dielman, T. E., “A comparison of forecasts from least absolute value and least squares regression”, J. Forecast. 5 (1986) 189–195; doi:10.1080/0094965042000223680.Google Scholar
Dielman, T. E., “Least absolute value regression: recent contributions”, J. Stat. Comput. Simul. 75 (2005) 263–286; doi:10.1002/for.3980050305.Google Scholar
Ghosh, D. and Chakraborty, D., “A new Pareto set generating method for multi-criteria optimization problems”, Oper. Res. Lett. 42 (2014) 514–521; doi:10.1016/j.orl.2014.08.011.Google Scholar
Hamacher, H. W., Pedersen, C. R. and Ruzika, S., “Finding representative systems for discrete bicriterion optimization problems”, Oper. Res. Lett. 35 (2007) 336–344; doi:10.1016/j.orl.2006.03.019.Google Scholar
Meinshausen, N. and Bühlmann, P., “High-dimensional graphs and variable selection with the Lasso”, Ann. Statist. 34 (2006) 1436–1462; doi:10.1214/009053606000000281.Google Scholar
Miller, A., Subset selection in regression, 2nd edn, Monogr. Statistics and Applied Probability (Chapman and Hall/CRC Press, Boca Raton, FL, 2002).Google Scholar
Miyashiroa, R. and Takanon, Y., “Mixed integer second-order cone programming formulations for variable selection in linear regression”, European J. Oper. Res. 247 (2015) 721–731; doi:10.1214/009053606000000281.Google Scholar
Papadimitriou, C. H. and Yannakakis, M., “On the approximability of trade-offs and optimal access of web sources”, in: Proceedings 41st Annual Symposium on Foundations of Computer Science (IEEE, Redondo Beach, CA, 2000) 86–92; doi:10.1109/SFCS.2000.892068.Google Scholar
Ren, Y. and Zhang, X., “Subset selection for vector autoregressive processes via adaptive Lasso”, Statist. Probab. Lett. 80 (2010) 1705–1712; doi:10.1016/j.spl.2010.07.013.Google Scholar
Sayın, S., “An algorithm based on facial decomposition for finding the efficient set in multiple objective linear programming”, Oper. Res. Lett. 19 (1996) 87–94; doi:10.1016/0167-6377(95)00046-1.Google Scholar
Schwertman, N. C., Gilks, A. J. and Cameron, J., “A simple noncalculus proof that the median minimizes the sum of the absolute deviations”, Amer. Statist. 44 (1990) 38–39; doi:10.1080/00031305.1990.10475690.Google Scholar
Stidsen, T., Andersen, K. A. and Dammann, B., “An algorithm based on facial decomposition for finding the efficient set in multiple objective linear programming”, Manag. Sci. 60 (2014) 1009–1032; doi:10.1287/mnsc.2013.1802.Google Scholar
Tibshirani, R., “Regression shrinkage and selection via the Lasso”, J. R. Stat. Soc. Ser. B 58 (1996) 267–288; https://www.jstor.org/stable/i316036.Google Scholar
Wolsey, L. A., Integer programming, 2nd edn (Wiley-Interscience, New York, 1998).Google Scholar
Zhang, C. and Huang, J., “The sparsity and bias of the Lasso selection in high-dimensional linear regression”, Ann. Statist. 36 (2008) 1567–1594; doi:10.1214/07-AOS520.Google Scholar