Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T23:53:48.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean flow induced by the viscous critical layer in a stratified fluid

Published online by Cambridge University Press:  17 February 2009

Noel Smyth
Noel Smyth
Affiliation:
Department of Applied Mathematics, University of New South Wales, P.O. Box 1, Kensington, N.S.W., Australia, 2033
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The evolution of the critical layer in a viscous, stratified fluid is examined in the limit of large Richardson and Reynolds numbers. A source far above the critical layer and of amplitude ɛ is turned on at t = 0 and the behaviour of both the steady state and transients is found. Viscosity dominates over nonlinearity in the critical layer for 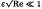, Re being an appropriately defined Reynolds number. Wave amplitudes are found to grow as the critical layer is approached, then decay rapidly due to the action of viscosity in a critical layer of O((Re)−1/3) around the critical level. The critical layer acts as a source of vorticity, which diffuses into the outer flow, resulting in an induced mean flow of 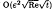. This induced mean flow causes the critical level to move towards the incoming wave.

Type
Research Article
Information
The ANZIAM Journal , Volume 29 , Issue 3 , January 1988 , pp. 352 - 373
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Baldwin, P. and Roberts, P. H., “The critical layer in stratified shear flow”, Mathematika 17 (1970) 102–119.CrossRefGoogle Scholar
[2]Booker, J. R. and Bretherton, F. P., “The critical layer for internal gravity waves in a shear flow”, J. Fluid Mech. 27 (1967) 513–539.CrossRefGoogle Scholar
[3]Brown, S. N., Rosen, A. S. and Maslowe, S. A., “The evolution of a quasi-steady critical layer in a stratified viscous shear flow”, Proc. Roy. Soc. London. Ser. A 375 (1981) 271–293.Google Scholar
[4]Brown, S. N. and Stewartson, K., “On the nonlinear reflexion of a gravity wave at a critical level, Part I”, J. Fluid Mech. 100 (1980) 577–595.CrossRefGoogle Scholar
[5]Brown, S. N. and Stewartson, K., “On the nonlinear reflexion of a gravity wave at a critical level, Part II”, J. Fluid Mech. 115 (1982) 217–230.CrossRefGoogle Scholar
[6]Brown, S. N. and Stewartson, K., “On the nonlinear reflexion of a gravity wave at a critical level, Part III”, J. Fluid Mech. 115 (1982) 231–250.CrossRefGoogle Scholar
[7]Dunkerton, T. J., “Wave transcience in a compressible atmosphere. Part II; Transient equatorial waves in a quasi-biennial oscillation”, J. Atmospheric Sci. 38 (1981) 281–297.2.0.CO;2>CrossRefGoogle Scholar
[8]Dunkerton, T. J., “Wave transcience in a compressible atmosphere, Part III: The saturation of internal gravity waves in the mesosphere”, J. Atmospheric Sci. 39 (1982) 1042–1051.Google Scholar
[9]Dunkerton, T. J. and Fritts, D. C., “Transient gravity wave-critical level interaction Part I: Convective adjustment and the mean zonal acceleration”, J. Atmospheric Sci. 41 (1984) 992–1007.2.0.CO;2>CrossRefGoogle Scholar
[10]Fritts, D. C. and Dunkerton, T. J., “A quasi-linear study of gravity wave saturation and self-acceleration”, J. Atmospheric Sci. 41 (1984)3272–3289.2.0.CO;2>CrossRefGoogle Scholar
[11]Grimshaw, R., “Internal gravity waves in a slowly varying, dissipative medium”, Geophys. Fluid Dyn. 6 (1974)131–148.CrossRefGoogle Scholar
[12]Grimshaw, R., “Nonlinear internal gravity waves and their interaction with the mean wind the mean wind” J. Atmospheric Sci. 32 (1975)1779–1793.2.0.CO;2>CrossRefGoogle Scholar
[13]Grimshaw, R., “Wave action and wave-mean flow interaction, with application to stratified shear flows” Ann. Rev. Fluid Mech. 16 (1984) 11–44.CrossRefGoogle Scholar
[14]Hazel, P., “The effect of viscosity and heat conduction on internal gravity waves at a critical level”, J. Fluid Mech. 30 (1967) 775–783.CrossRefGoogle Scholar