No CrossRef data available.
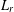 $L_{r}$ CONVERGENCE AND WEAK LAWS OF LARGE NUMBERS FOR
$L_{r}$ CONVERGENCE AND WEAK LAWS OF LARGE NUMBERS FOR 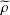 $\widetilde{\unicode[STIX]{x1D70C}}$-MIXING RANDOM VARIABLES
$\widetilde{\unicode[STIX]{x1D70C}}$-MIXING RANDOM VARIABLESPublished online by Cambridge University Press: 19 April 2017
The 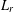 $L_{r}$ convergence and a class of weak laws of large numbers are obtained for sequences of
$L_{r}$ convergence and a class of weak laws of large numbers are obtained for sequences of 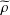 $\widetilde{\unicode[STIX]{x1D70C}}$-mixing random variables under the uniform Cesàro-type condition. This is weaker than the
$\widetilde{\unicode[STIX]{x1D70C}}$-mixing random variables under the uniform Cesàro-type condition. This is weaker than the 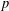 $p$th-order Cesàro uniform integrability.
$p$th-order Cesàro uniform integrability.