Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T03:25:37.796Z Has data issue: false hasContentIssue false
  • English
  • Français

ITERATED LAVRENTIEV REGULARIZATION FOR NONLINEAR ILL-POSED PROBLEMS

Part of: Numerical analysis in abstract spaces Partial differential equations, initial value and time-dependent initial-boundary value problems General theory of linear operators

Published online by Cambridge University Press:  19 April 2010

P. MAHALE  and
M. T. NAIR
P. MAHALE
Affiliation:
Department of Mathematics, I.I.T. Madras, Chennai - 600036, India (email: [email protected], [email protected])
M. T. NAIR*
Affiliation:
Department of Mathematics, I.I.T. Madras, Chennai - 600036, India (email: [email protected], [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider an iterated form of Lavrentiev regularization, using a null sequence (αk) of positive real numbers to obtain a stable approximate solution for ill-posed nonlinear equations of the form F(x)=y, where F:D(F)⊆X→X is a nonlinear operator and X is a Hilbert space. Recently, Bakushinsky and Smirnova [“Iterative regularization and generalized discrepancy principle for monotone operator equations”, Numer. Funct. Anal. 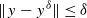Optim.28 (2007) 13–25] considered an a posteriori strategy to find a stopping index kδ corresponding to inexact data yδ with resulting in the convergence of the method as δ→0. However, they provided no error estimates. We consider an alternate strategy to find a stopping index which not only leads to the convergence of the method, but also provides an order optimal error estimate under a general source condition. Moreover, the condition that we impose on (αk) is weaker than that considered by Bakushinsky and Smirnova.

Keywords

Lavrentiev regularizationnonlinear ill-posed problemsmonotone operatorFréchet derivativeregularization parameterstopping indexGauss–Newton methodsource functiongeneral source conditionorder optimal result

MSC classification

Secondary: 47A52: Ill-posed problems, regularization 65J15: Equations with nonlinear operators (do not use ) 65J22: Inverse problems 65M30: Improperly posed problems
Type
Research Article
Information
The ANZIAM Journal , Volume 51 , Issue 2 , October 2009 , pp. 191 - 217
Copyright
Copyright © Australian Mathematical Society 2010

References

[1]Bakushinsky, A. and Smirnova, A., “On application of generalized discrepancy principle to iterative methods for nonlinear ill-posed problems”, Numer. Funct. Anal. Optim. 26 (2005) 35–48.CrossRefGoogle Scholar
[2]Bakushinsky, A. and Smirnova, A., “A posteriori stopping rule for regularized fixed point iterations”, Nonlinear Anal. 64 (2006) 1255–1261.CrossRefGoogle Scholar
[3]Bakushinsky, A. and Smirnova, A., “Iterative regularization and generalized discrepancy principle for monotone operator equations”, Numer. Funct. Anal. Optim. 28 (2007) 13–25.CrossRefGoogle Scholar
[4]Binder, A., Engl, H. W., Groetsch, C. W., Neubauer, A. and Scherzer, O., “Weakly closed nonlinear operators and parameter identification in parabolic equations by Tikhonov regularization”, Appl. Anal. 55 (1994) 215–235.Google Scholar
[5]Deimling, K., Nonlinear functional analysis (Springer-Verlag, New York, 1985).CrossRefGoogle Scholar
[6]Engl, H. W., Hanke, M. and Neubauer, A., Regularization of inverse problems,Volume 375 of Mathematics and its Applications (Kluwer, Dordrecht, 1996).CrossRefGoogle Scholar
[7]Engl, H. W., Kunish, K. and Neubauer, A., “Convergent rates for Tikhonov regularisation of nonlinear ill-posed problems”, Inverse Problems 5 (1989) 523–540.CrossRefGoogle Scholar
[8]Hohage, T., “Iterative methods in inverse obstacle scattering: regularization theory of linear and nonlinear exponentially ill-posed problems” Ph. D. Thesis, University of Linz, 1999.Google Scholar
[9]Hohage, T., “Regularization of exponentially ill-posed problem”, Numer. Funct. Anal. Optim. 21 (2000) 439–464.CrossRefGoogle Scholar
[10]Jin, Q., “On the iteratively regularized Gauss–Newton method for solving nonlinear ill-posed problems”, Math. Comp. 69 (2000) 1603–1623.Google Scholar
[11]Jin, Q. and Hou, Zong-Yi, “On the choice of the regularization parameter for ordinary and iterated Tikhonov regularization of nonlinear illposed problems”, Inverse Problems 13 (1997) 815–827.CrossRefGoogle Scholar
[12]Jin, Q. and Hou, Zong-Yi, “On an a posteriori parameter choice strategy for Tikhonov regularization of nonlinear ill-posed problems”, Numer. Math. 83 (1999) 139–159.Google Scholar
[13]Mahale, P. and Nair, M. T., “General source conditions for nonlinear ill-posed equations”, Numer. Funct. Anal. Optim. 28 (2007) 111–126.CrossRefGoogle Scholar
[14]Nair, M. T. and Tautenhahn, U., “Lavrentiev regularization for linear ill-posed problems under general source conditions”, Z. Anal. Anwendungen 23 (2004) 167–185.CrossRefGoogle Scholar
[15]Scherzer, O., Engl, H. W. and Kunisch, K., “Optimal a posteriori parameter choice for Tikhonov regularization for solving nonlinear ill-posed problems”, SIAM J. Numer. Anal. 30 (1993) 1796–1838.CrossRefGoogle Scholar
[16]Tautenhahn, U., “On the method of Lavrentiev regularization for nonlinear ill-posed problems”, Inverse Problems 18 (2002) 191–207.CrossRefGoogle Scholar
[17]Tautenhahn, U., “Lavrentiev regularization of nonlinear ill-posed problems”, Vietnam J. Math. 32 (2004) 29–41.Google Scholar
[18]Tautenhahn, U. and Jin, Q., “Tikhonov regularization and a posteriori rules for solving nonlinear ill posed problems”, Inverse Problems 19 (2003) 1–21.CrossRefGoogle Scholar