Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T07:09:55.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Inversion of the Struve transform of half integer order

Published online by Cambridge University Press:  17 February 2009

B. H. J. McKellar ,
M. A. Box  and
E. R. Love
B. H. J. McKellar
Affiliation:
School of Physics, University of Melbourne, Parkville, Victoria 3052 (permanent address) and Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, U.S.A.
M. A. Box
Affiliation:
School of Physics, University of New South Wales, Kensington, N.S.W. 2033.
E. R. Love
Affiliation:
Department of Mathematics, University of Melbourne, Parkville, Victoria 3052.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Defining a spherical Struve function 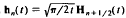we show that the Struve transform of half integer order, or spherical Struve transform,

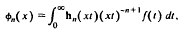
where n is a non-negative integer, may under suitable conditions be solved for f(t):

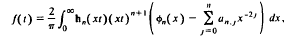
where 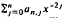is the sum of the first n + 1 terms in the asymptotic expansion of φn(x) as x → ∞. The coefficients in the asymptotic expansion are identified as

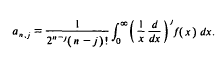
It is further shown that functions φn (x) which are representable as spherical Struve transforms satisfy n + 1 integral constraints, which in turn allow the construction of many equivalent inversion formulae.

Type
Research Article
Information
The ANZIAM Journal , Volume 25 , Issue 2 , October 1983 , pp. 161 - 174
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Abramowitz, M. and Stegun, I. A. (eds.), Handbook of mathematical functions (Dover, New York, 1970).Google Scholar
[2]Box, M. A. and McKellar, B. H. J., “A generalised inversion theorem for the Struve transfrom with application to scattering by polydispersion”, University of Melbourne preprint UM-P-77/11 (1977), 9 pages.Google Scholar
[3]Box, M. A. and McKellar, B. H. J., “Analytical inversion of multispectral extinction data in the anomalous diffraction approximation”, Optics Lett. 3 (1978), 91–93.CrossRefGoogle ScholarPubMed
[4]Box, M. A. and McKellar, B. H. J., “Relationship between two analytic inversion formulae for multispectral extinction data”, Appl. Optics 18 (1979), 3599–3601.CrossRefGoogle ScholarPubMed
[5]Box, M. A. and McKellar, B. H. J., “Further relations between analytic inversion formulae for multispectral extinction data”, Appl. Optics 20 (1981), 3829–3831.CrossRefGoogle ScholarPubMed
[6]Cooke, R. G., “The inversion formulae of Hardy and Titchmarsh”, Proc. London Math. Soc. (2) 24 (1925), 381–420.Google Scholar
[7]Fox, C., “A generalisation of the Fourier-Bessel transform”, Proc. London Math. Soc. (2) 29, (1929), 401–452.CrossRefGoogle Scholar
[8]Fymat, A. L., “Analytical inversions in remote sensing of particle size distributions. 1: Multispectral extinctions in the anomalous diffraction approximation”, Appl. Optics 17 (1978). 1675–1676.Google ScholarPubMed
[9]Fymat, A. L., “A generalisation of Cooke's integral inversion formula with application to remote sensing theory”, Appl. Math. Comput. 5 (1979), 23–39.Google Scholar
[10]Gradshteyn, I. S. and Ryzhik, I. M.. Tables of integrals, series and products (Academic, New York, 1980).Google Scholar
[11]Hardy, G. H., “Some formulae in the theory of Bessel functions”. Proc. London Math. Soc. (2) 23 (1925), lxi–lxiii.Google Scholar
[12]McKellar, B. H. J., “Light-scattering determination of the size distribution of cylinders: an analytic approximation”, J. Opt. Soc. Amer. 72 (1982), 671–672.CrossRefGoogle Scholar
[13]Perelman, A. Ya. and Shifrin, K. S., “Improvements to the spectral transparency method for determining particle size distribution”, Appl. Optics 19 (1980), 1787–1793.CrossRefGoogle Scholar
[14]Titchniarsh, E. C., “A pair of inversion formulae”, Proc. London Math. Soc. (2) 23 (1923), xxxiv–xxxv.Google Scholar
[15]Titchmarsh, E. C., Theory of Fourier integrals, 2nd ed. (Oxford University Press, Oxford, 1948).Google Scholar
[16]Watson, G. N., A treatise on the theory of Bessel functions. 2nd ed. (Cambridge University Press, Cambridge. 1966).Google Scholar