Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T19:36:56.644Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FORMATION OF LARGE-AMPLITUDE FINGERS IN ATMOSPHERIC VORTICES

Part of: Basic methods in fluid mechanics Incompressible inviscid fluids

Published online by Cambridge University Press:  28 March 2016

JASON M. COSGROVE  and
LAWRENCE K. FORBES
JASON M. COSGROVE*
Affiliation:
School of Physical Sciences, Discipline of Mathematics, University of Tasmania, Private Bag 37, Hobart Tasmania, 7001Australia email [email protected], [email protected]
LAWRENCE K. FORBES
Affiliation:
School of Physical Sciences, Discipline of Mathematics, University of Tasmania, Private Bag 37, Hobart Tasmania, 7001Australia email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Large-scale low-pressure systems in the atmosphere are occasionally observed to possess Kelvin–Helmholtz fingers, and an example is shown in this paper. However, these structures are hundreds of kilometres long, so that they are necessarily affected strongly by nonlinearity. They are evidently unstable and are observed to dissipate after a few days.

A model for this phenomenon is presented here, based on the usual 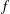$f$-plane equations of meteorology, assuming an atmosphere governed by the ideal gas law. Large-amplitude perturbations are accounted for, by retaining the equations in their nonlinear forms, and these are then solved numerically using a spectral method. Finger formation is modelled as an initial perturbation to the $n$th Fourier mode, and the numerical results show that the fingers grow in time, developing structures that depend on the particular mode. Results are presented and discussed, and are also compared with the predictions of the 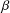${\it\beta}$-plane theory, in which changes of the Coriolis acceleration with latitude are included. An idealized vortex in the northern hemisphere is considered, but the results are at least in qualitative agreement with an observation of such systems in the southern hemisphere.

Keywords

atmospheric vorticesspectral methodsf-plane𝛽-plane

MSC classification

Primary: 76B60: Atmospheric waves
Secondary: 76M22: Spectral methods
Type
Research Article
Information
The ANZIAM Journal , Volume 57 , Issue 4 , April 2016 , pp. 395 - 416
Copyright
© 2016 Australian Mathematical Society 

References

Baker, G. R. and Pham, L. D., “A comparison of blob methods for vortex sheet roll-up”, J. Fluid Mech. 547 (2006) 297–316; doi:10.1017/S0022112005007305.Google Scholar
Caflisch, R. E., Li, X. and Shelley, M. J., “The collapse of an axi-symmetric, swirling vortex sheet”, Nonlinearity 6 (1993) 843–867; doi:10.1088/0951-7715/6/6/001.Google Scholar
Chandrasekhar, S., Hydrodynamic and hydromagnetic stability (Dover, New York, 1981).Google Scholar
Chen, M. J. and Forbes, L. K., “Accurate methods for computing inviscid and viscous Kelvin–Helmholtz instability”, J. Comput. Phys. 230 (2011) 1499–1515 doi:10.1016/j.jcp.2010.11.017.CrossRefGoogle Scholar
Cowley, S. J., Baker, G. R. and Tanveer, S., “On the formation of Moore curvature singularities in vortex sheets”, J. Fluid Mech. 378 (1999) 233–267; doi:10.1017/S0022112098003334.Google Scholar
Crapper, G. D., Dombrowski, N. and Pyott, G. A. D., “Kelvin–Helmholtz wave growth on cylindrical sheets”, J. Fluid Mech. 68 (1975) 497–502; doi:10.1017/S0022112075001784.Google Scholar
Drazin, P. G. and Reid, W. H., Hydrodynamic stability, 2nd edn. (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Forbes, L. K., “The Rayleigh–Taylor instability for inviscid and viscous fluids”, J. Engrg. Math. 65 (2009) 273–290; doi:10.1007/s10665-009-9288-9.CrossRefGoogle Scholar
Forbes, L. K., “A cylindrical Rayleigh–Taylor instability: radial outflow from pipes or stars”, J. Engrg. Math. 70 (2011) 205–224; doi:10.1007/s10665-010-9374-z.Google Scholar
Forbes, L. K. and Cosgrove, J. M., “A line vortex in a two-fluid system”, J. Engrg. Math. 84 (2014) 181–199; doi:10.1007/s10665-012-9606-5.CrossRefGoogle Scholar
Holton, J. R., An introduction to dynamic meteorology, 3rd edn. (Academic Press, Cambridge, 1992).Google Scholar
Kay, J. M. and Nedderman, R. M., Fluid mechanics and transfer processes (Cambridge University Press, Cambridge, 1985).Google Scholar
Krasny, R., “Desingularization of periodic vortex sheet roll-up”, J. Comput. Phys. 65 (1986) 292–313; doi:10.1016/0021-9991(86)90210-X.CrossRefGoogle Scholar
Lipps, F. B., “A note on the beta-plane approximation”, Tellus 16 (1964) 535–537 doi:10.1111/j.2153-3490.1964.tb00190.x.CrossRefGoogle Scholar
Matsuoka, C. and Nishihara, K., “Analytical and numerical study on a vortex sheet in incompressible Richtmyer–Meshkov instability in cylindrical geometry”, Phys. Rev. E 74 (2006) 066303–066314; doi:10.1103/PhysRevE.74.066303.CrossRefGoogle Scholar
Moore, D. W., “The spontaneous appearance of a singularity in the shape of an evolving vortex sheet”, Proc. R. Soc. Lond. A 365 (1979) 105–119 doi:10.1098/rspa.1979.0009.Google Scholar
Vallis, G. K., Atmospheric and oceanic fluid dynamics (Cambridge University Press, Cambridge, 2006).Google Scholar
von Winckel, G., lgwt.m, at: MATLAB file exchange website,http://www.mathworks.com/matlabcentral/fileexchange/4540-legendre-gauss-quadrature-weights-and-nodes, 2004.Google Scholar