Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T06:50:11.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast diffusion with loss at infinity—additional solutions

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theoretical Physics, Research School of Physical Sciences, Australian National University, Canberra ACT 0200, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper presents some additional solutions of the diffusion equation

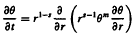
for the case s = 2, m = −1, a case that was left open in a previous discussion. These solutions behave in a manner that is physically acceptable as the time, t, increases and as the radial coordinate, r, tends to infinity.

Type
Research Article
Information
The ANZIAM Journal , Volume 42 , Issue 3 , January 2001 , pp. 445 - 450
Copyright
Copyright © Australian Mathematical Society 2001

References

[1] Crank, J., The Mathematics of Diffusion, 2nd ed., Chapter 7 (Clarendon Press, Oxford, 1975).Google Scholar
[2] Edwards, M. P. and Broadbridge, P., “Exact transient solutions to nonlinear diffusion-convection equations in higher dimensions”, J. Phys. A: Math. Gen. 27 (1994) 5455–5465.CrossRefGoogle Scholar
[3] King, J. R., “Exact similarity solutions to some nonlinear diffusion equations”, J. Phys. A: Math. Gen. 23 (1990) 3681–3697.CrossRefGoogle Scholar
[4] Lacey, A. A., Ockendon, J. R. and Tayler, A. B., “Waiting-time solutions of a non-linear diffusion equation”, SIAM J. Appl. Math. 42 (1982) 1252–1264.CrossRefGoogle Scholar
[5] Lonngren, K. E. and Hirose, A., “Expansion of an electron cloud”, Phys. Lett. 59A (1976) 285–286.CrossRefGoogle Scholar
[6] Philip, J. R., “Fast diffusion with loss at infinity”, J. Austral. Math. Soc. Ser. B 36 (1995) 438–459.CrossRefGoogle Scholar
[7] Webb, G. M. and Gleeson, L. J., “Green's theorem and functions for the steady-state cosmic-ray equation of transport”. Astrophysics and Space Science 50 (1977) 205–233.CrossRefGoogle Scholar