No CrossRef data available.
Article contents
Critical values for a nonlinear difference equation
Published online by Cambridge University Press: 17 February 2009
Abstract
The paper discusses equilibrium solutions and solutions with period two and period three for the difference equation
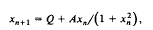
where Q and A are real, positive parameters. The equation was used by Bier and Bountis [1] as an example of a difference equation whose iteration diagram can show bubbles of finite length rather than the successive bifurcations usually expected. The paper examines in more detail what kind of solution can occur for given values of Q and A and establishes a series of critical curves which demarcate the regions in the (Q, A) plane where solutions of period two or period three occur and the subregions where these periodic solutions are stable. This makes it easy to see how Q and A can be combined into a one-parameter equation which gives a bubble, or a series of bubbles, in the iteration diagram.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1987


