Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T01:05:37.539Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CONTROLLER DESIGN FOR SINGULAR FRACTIONAL-ORDER SYSTEMS WITH FRACTIONAL ORDER 0 <α< 1

Part of: Stability

Published online by Cambridge University Press:  25 September 2018

T. ZHAN  and
S. P. MA Open the ORCID record for S. P. MA [Opens in a new window]
T. ZHAN
Affiliation:
School of Mathematics, Shandong University, Jinan, 250100, China email [email protected], [email protected]
S. P. MA*
Affiliation:
School of Mathematics, Shandong University, Jinan, 250100, China email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the problem of pseudostate and static output feedback stabilization for singular fractional-order linear systems with fractional order $\unicode[STIX]{x1D6FC}$ when 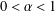$0<\unicode[STIX]{x1D6FC}<1$. All the results are given by linear matrix inequalities. First, a new sufficient and necessary condition for the admissibility of singular fractional-order systems is presented. Then based on the admissible result, not only are sufficient conditions for designing pseudostate and static output feedback controllers obtained, but also sufficient and necessary conditions are presented by using different methods that guarantee the admissibility of the closed-loop systems. Finally, the effectiveness of the proposed approach is demonstrated by numerical simulations and a real-world example.

Keywords

admissibilityfeedback controlsingular fractional-order systemslinear matrix inequalities

MSC classification

Primary: 93D15: Stabilization of systems by feedback
Type
Research Article
Information
The ANZIAM Journal , Volume 60 , Issue 2 , October 2018 , pp. 230 - 248
Copyright
© 2018 Australian Mathematical Society 

References

Chang, X. H., Park, J. H. and Tang, Z., “New approach to $H_{\infty }$ filtering for discrete-time systems with polytopic uncertainties”, Signal Process. 113 (2015) 147–158; doi:10.1016/j.sigpro.2015.02.002.Google Scholar
Chen, L., Basu, B. and McCabe, D., “Fractional order models for system identification of thermal dynamics of buildings”, Energy Buildings 133 (2016) 381–388; doi:10.1016/j.enbuild.2016.09.006.Google Scholar
Farges, C., Sabatier, J. and Moze, M., “Pseudo-state feedback stabilization of commensurate fractional order systems”, Automatica 46 (2010) 1730–1734; doi:10.1016/j.automatica.2010.06.038.Google Scholar
Guo, T. L., “Controllability and observability of impulsive fractional linear time-invariant system”, Comput. Math. Appl. 64 (2012) 3171–3182; doi:10.1016/j.camwa.2012.02.020.Google Scholar
Ibrir, S. and Bettayeb, M., “New sufficient conditions for observer-based control of fractional order uncertain systems”, Automatica 59 (2015) 216–223; doi:10.1016/j.automatica.2015.06.002.Google Scholar
Ichise, M., Nagayanagi, Y. and Kojima, T., “An analog simulation of non-integer order transfer functions for analysis of elec-trode processes”, J. Electroanal. Chem. Interfacial Electrochem. 33 (1971) 253–265; doi:10.1016/S0022-0728(71)80115-8.Google Scholar
Ji, Y. and Qiu, J. Q., “Stabilization of fractional-order singular uncertain systems”, ISA Trans. 56 (2015) 53–64; doi:10.1016/j.isatra.2014.11.016.Google Scholar
Kaczorek, T., “Singular fractional linear systems and electrical circuits”, Int. J. Appl. Math. Comput. Sci. 21 (2011) 379–384; doi:10.2478/v10006-011-0028-8.Google Scholar
Li, Y., Chen, Y. Q. and Podlubny, I., “Mittag-leffler stability of fractional order nonlinear dynamic systems”, Automatica 45 (2009) 1965–1969; doi:10.1016/j.automatica.2009.04.003.Google Scholar
Lu, J. G. and Chen, Y. Q., “Robust stability and stabilization of fractional order interval systems with the fractional order $\unicode[STIX]{x1D6FC}$ : the $0<\unicode[STIX]{x1D6FC}<1$ case”, IEEE Trans. Automat. Control 55 (2010) 152–158; doi:10.1109/TAC.2009.2033738.Google Scholar
Marir, S., Chadli, M. and Bouagada, D., “New admissibility conditions for singular linear continuous-time fractional-order systems”, J. Franklin Inst. 354 (2017) 752–766; doi:10.1016/j.jfranklin.2016.10.022.Google Scholar
Marir, S., Chadli, M. and Bouagada, D., “A novel approach of admissibility for singular linear continuous-time fractional-order systems”, Int. J. Control Autom. Syst. 15 (2017) 959–964; doi:10.1007/s12555-016-0003-0.Google Scholar
Mcadams, T. E., Lackermeier, A., Mclaughlin, J. A., Macken, D. and Jossinet, J., “The linear and non-linear electrical properties of the electrode-electrolyte interface”, Biosens. Bioelectron. 10 (1995) 67–74; doi:10.1016/0956-5663(95)96795-Z.Google Scholar
N’Doye, I., Daarouach, M., Zasadzinski, M. and Radhy, N. E., “Robust stabilization of uncertain descriptor fractional order systems”, Automatica 49 (2013) 1907–1913; doi:10.1016/j.automatica.2013.02.066.Google Scholar
Oldham, B. K. and Spanier, J., The fractional calculus (Academic Press, New York and London, 1974).Google Scholar
Petráš, I., Fractional-order nonlinear systems: modeling, analysis and simulation (Springer Science & Business Media, Higher Education Press, Beijing, 2011).Google Scholar
Podlubny, I., Fractional differential equations (Academic Press, New York, 1999).Google Scholar
Wei, Y. H., Du, B. and Wong, Y., “Necessary and sufficient admissibility condition of singular fractional order systems”, in: The 35th Chinese control conference (Chengdu, China, 2016) 85–88; doi:10.1109/ChiCC.2016.7553065; July.Google Scholar
Wei, X., Liu, D. Y. and Boutat, D., “Nonasymptotic pseudo-state estimation for a class of fractional order linear systems”, IEEE Trans. Automat. Control 62 (2017) 1150–1164; doi:10.1109/TAC.2016.2575830.Google Scholar
Xu, J., Study on some problems in analysis and control of fractional order systems (Master’s Thesis, Shanghai Jiao Tong University, Shanghai, 2009).Google Scholar
Xu, S. and Lam, J., “Robust stability and stabilization of discrete singular systems: an equivalent characterization”, IEEE Trans. Automat. Control 49 (2004) 568–574; doi:10.1109/TAC.2003.822854.Google Scholar
Xu, S. and Lam, J., Robust control and filtering of singular systems (Springer, Berlin Heidelberg, 2006).Google Scholar
Yin, C., Zhong, S. M., Huang, X. G. and Chen, Y. H., “Robust stability analysis of fractional order uncertain singular nonlinear system with external disturbance”, Appl. Math. Comput. 269 (2015) 351–362; doi:10.1016/j.amc.2015.07.059.Google Scholar
Yu, Y., Jiao, Z. and Sun, C. Y., “Sufficient and necessary condition of admissibility for fractional-order singular system”, Acta Automat. Sinica 39 (2013) 2160–2164; doi:10.1016/S1874-1029(14)60003-3.Google Scholar
Zhan, T., Tian, J. M. and Ma, S. P., “Full-order and reduced-order observer design for one-sided Lipschitz nonlinear fractional order systems with unknown input”, Int. J. Control Automat. Syst. (2018) 1–11; doi:10.1007/s12555-017-0684-z.Google Scholar
Zhang, X. F. and Chen, Y. Q., “Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order $\unicode[STIX]{x1D6FC}$ : the $0<\unicode[STIX]{x1D6FC}<1$ case”, ISA Trans. (2017); doi:10.1016/j.isatra.2017.03.008.Google Scholar
Zhu, S. Q., Zhang, C. H., Liu, X. Z. and Li, Z. B., “Delay-dependent robust $H_{\infty }$ control for singular systems with multiple delays”, ANZIAM J. 50 (2008) 209–230; doi:10.1017/S1446181109000121.Google Scholar