Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T05:11:53.603Z Has data issue: false hasContentIssue false
  • English
  • Français

Chaotic breakdown of a periodically forced, weakly damped pendulum

Published online by Cambridge University Press:  17 February 2009

Peter J. Bryant
Peter J. Bryant
Affiliation:
Department of Mathematics, University of Canterbury, Christchurch, New Zealand.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An investigation is made of the transition from periodic solutions through nearly-periodic solutions to chaotic solutions of the differential equation governing forced coplanar motion of a weakly damped pendulum. The pendulum is driven by horizontal, periodic forcing of the pivot with maximum acceleration Є g and dimensionless frequency ω As the forcing frequency ω is decreased gradually at a sufficiently large forcing amplitude Є, it has been shown previously that the pendulum progresses from symmetric oscillations of period T (= 2 π/ω) into a symmetry-breaking, period-doubling sequence of stable, periodic oscillations. There are two related forms of asymmetric, stable oscillations in the sequence, dependent on the initial conditions. When the frequency is decreased immediately beyond the sequence, the oscillations become unstable but remain in the neighbourhood in (θ,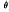) phase space of one or other of the two forms of periodic oscillations, where θ(t) is the pendulum angle with the downward vertical. As the frequency is decreased further, the oscillations move intermittently between the neighbourhoods in (θ,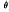) phase space of each of the two forms of periodic oscillations, in paired nearly-periodic oscillations. Further decrease of the forcing frequency leads to time intervals in which the motion is strongly unstable, with the pendulum passing intermittently over the pivot, interspersed with time intervals when the motion is nearly-periodic and only weakly unstable. The strongly-unstable intervals dominate in fully chaotic oscillations. Windows of independent, stable, periodic oscillations occur throughout the frequency range investigated. It is shown in an appendix how the Floquet method may be interpreted to describe the linear stability of the periodic and nearly-periodic solutions, and the windows of periodic oscillations in the investigated frequency range are listed in a second appendix.

Type
Research Article
Information
The ANZIAM Journal , Volume 34 , Issue 2 , October 1992 , pp. 153 - 173
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Baker, Gregory L. and Gollub, Jerry P., Chaotic Dynamics (Cambridge University Press, Cambridge, 1990).Google Scholar
[2]Berger, Eberhard and Wille, Rudolf, “Periodic flow phenomena”, Ann. Rev. Fluid Mech. 4 (1972) 313–340.CrossRefGoogle Scholar
[3]Bryant, Peter J. and Miles, John W., “On a periodically-forced, weakly damped pendulum: Part 2: Horizontal forcing”, J. Austral. Math. Soc. Ser. B. 32 (1990) 23–41.CrossRefGoogle Scholar
[4]Feigenbaum, Mitchell J., “Quantitative universality for a class of nonlinear transformations”, J. Stat. Phys. 19 (1978), 25–52.CrossRefGoogle Scholar
[5]Gwinn, E. G. and Westervelt, R. M., “Fractal basin boundaries and intermittency in the driven pendulum”, Phys. Rev. A. 33 (1986) 4143–55.CrossRefGoogle Scholar
[6]Tritton, D. J., “A note on vortex streets behind circular cylinders at low Reynolds number”, J. Fluid Mech. 45 (1971) 203–8.CrossRefGoogle Scholar