Article contents
ASYMPTOTIC BEHAVIOUR OF A CLASS OF RESOURCE COMPETITION BIOLOGY SPECIES SYSTEM BY THE FRACTIONAL BROWNIAN MOTION
Published online by Cambridge University Press: 15 May 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We analyse the asymptotic behaviour of a biological system described by a stochastic competition model with  $n$ species and
$n$ species and 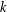 $k$ resources (chemostat model), in which the species mortality rates are influenced by the fractional Brownian motion of the extrinsic noise environment. By constructing a Lyapunov functional, the persistence and extinction criteria are derived in the mean square sense. Some examples are given to illustrate the effectiveness of the theoretical result.
$k$ resources (chemostat model), in which the species mortality rates are influenced by the fractional Brownian motion of the extrinsic noise environment. By constructing a Lyapunov functional, the persistence and extinction criteria are derived in the mean square sense. Some examples are given to illustrate the effectiveness of the theoretical result.
MSC classification
Primary:
92D30: Epidemiology
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Society
References
Fan, Y., Scheibea, T. D., Mahadevan, R., Garg, S. and Long, P. E., “Direct coupling of a genome-scale microbial in silico model and a groundwater reactive transport model”, J. Contaminant Hydrol.
122 (2011) 96–103; doi:10.1016/j.jconhyd.2010.11.007.Google Scholar
Fowler, A. C., Winstanley, H. F. and Cribbin, L. B., “Oscillations in soil bacterial redox reactions”, J. Theoret. Biol.
342 (2014) 33–38; doi:10.1016/j.jtbi.2013.10.010.CrossRefGoogle ScholarPubMed
Huisman, J. and Weissing, F. J., “Biodiversity of plankton by species oscillations and chaos”, Nature
402 (1999) 407–410; doi:10.1038/46540.Google Scholar
Ji, C. and Jiang, D., “Threshold behaviour of a stochastic SIR model”, Appl. Math. Model.
38 (2014) 5067–5079; doi:10.1016/j.apm.2014.03.037.Google Scholar
Khan, A. A., Zytner, R. G. and Feng, Z., “Establishing correlations and scale-up factor for estimating the petroleum biodegradation rate in soil”, Bioremediation J.
19 (2015) 32–46; doi:10.1080/10889868.2014.933173.Google Scholar
Khasminskii, R., “Stochastic stability of differential equations”, Stochastic modelling and applied probability, volume 66, 2nd edn (Springer, Berlin, 2012).Google Scholar
Li, B. and Smith, H. L., “Global dynamics of microbial competition for two resources with internal storage”, J. Math. Biol.
55 (2007) 481–515; doi:10.1007/s00285-007-0092-8.Google Scholar
Li, D. and Zhu, Q., “Comparison principle and stability of stochastic delayed neural networks with Markovian switching”, Neurocomputing
123 (2014) 436–442; doi:10.1016/j.neucom.2013.07.039.Google Scholar
Monod, J., “La technique de culture continue; théorie et applications”, Ann. Inst. Pasteur
79 (1950) 390–401; https://www.cabdirect.org/cabdirect/abstract/19512703495.Google Scholar
Xu, C. and Yuan, S., “Competition in the chemostat: a stochastic multi-species model and its asymptotic behavior”, Math. Biosci.
280 (2016) 1–9; doi:10.1016/j.mbs.2016.07.008.Google Scholar
Zheng, D. W., Bengtsson, J. and Agren, G. I., “How do soil organisms affect total organic nitrogen storage and substrate nitrogen to carbon ratio in soils? A theoretical analysis”, Oikos
86 (1999) 430–442; doi:10.2307/3546648.Google Scholar
- 1
- Cited by


