Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-04T19:30:26.308Z Has data issue: false hasContentIssue false
  • English
  • Français

An evolutionary monotone follower problem in [0, 1]

Published online by Cambridge University Press:  17 February 2009

Min Sun
Min Sun
Affiliation:
Department of Applied Mathematical Sciences, University of Houston, Texas 77002, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider in this article an evolutionary monotone follower problem in [0,1]. State processes under consideration are controlled diffusion processes 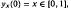, solutions of dyx(t) = g(yx(t), t)dt + σu(yx(t), t) dwt + dυt with yx(0) = x ∈[0, 1], where the control processes υt are increasing, positive, and adapted. The cost functional is of integral type, with certain explicit cost of control action including the cost of jumps. We shall present some analytic results of the value function, mainly its characterisation, by standard dynamic programming arguments.

Type
Research Article
Information
The ANZIAM Journal , Volume 31 , Issue 1 , July 1989 , pp. 97 - 107
Copyright
Copyright © Australian Mathematical Society 1989

References

[1] Bather, J. A. and Chernoff, H., “Sequential decisions in the control of a spaceship”, Proc. Fifth Berkeley Sympos. Mathematical Statistics and Probability, 3 (Univ. Calif. Press, Berkeley, 1967) 181–207.Google Scholar
[2] Bather, J. A. and Chernoff, H., “Sequential decisions in the control of a spaceship (finite fuel)”, J. Appl. Probab. 4 (1967) 584–604.Google Scholar
[3] Beneš, V. E., Shepp, L. A. and Witsenhausen, H. S., “Some solvable stochastic control problems”, Stochastics 4 (1980) 39–83.Google Scholar
[4] Chow, P. L., Menaldi, J. L. and Robin, M., “Additive control of stochastic linear systems with finite horizon”, SIAM J. Control Optim. 23 (1985) 858–899.CrossRefGoogle Scholar
[5] Friedman, A., Partial differential equations of parabolic type (Prentice-Hall, Inc., Englewood Cliffs, 1964).Google Scholar
[6] Sun, M., “Singular control problems in bounded intervals”, Stochastics 21 (1987) 303–344.Google Scholar